🌟 前言
大家好,我是Edison😎
之前有写过一篇关于「冒泡排序」的文章;
但是冒泡排序的实现仍然不是最优,有一种排序算法叫做 「鸡尾酒排序」;
鸡尾酒排序是基于冒泡排序的一种升级;
今天这篇文章就是关于 「鸡尾酒排序」 的详细介绍;
Let‘s get it!
🛫送所有正在努力的大家一句话:你不一定逆风翻盘,但一定要向阳而生🌅
🔥热榜必看文章:室友打一把王者就学会了冒泡排序算法

文章目录
1. 基本思想
鸡尾酒排序又叫「快乐小时排序」;它基于冒泡排序做了一点小小优化;
让我们首先来回顾一下冒泡排序的思想:
冒泡排序的每⼀个元素都可以像⼩⽓泡⼀样,根据⾃⾝⼤⼩,⼀点⼀点地向着数组的⼀侧移动。
算法的每⼀轮都是从左到右来⽐较元素, 进⾏单向的位置交换的 。
那么鸡尾酒排序做了怎样的优化呢?
鸡尾酒排序的元素比较和交换过程是双向的
2. 图解示例
让我们来举一个栗子:
有8个数组成一个无序数列:2,3,4,5,6,7,8,1,希望从小到大排序。
如果按照冒泡排序的思想,排序的过程是什么样呢?
🍑 冒泡过程
第一轮结果(8和1交换)
第二轮结果(7和1交换)
第三轮结果(6和1交换)
第四轮结果(5和1交换)
第五轮结果(4和1交换)
第六轮结果(3和1交换)
第七轮结果(2和1交换)
那么冒泡排序有什么问题呢???
由上面可以看出,从2到8已经是有序了。只有元素1的位置不对,却还要进行7轮排序,太麻烦了吧?
那我们的鸡尾酒排序正是要解决这种问题,让我们来看一看鸡尾酒排序的过程吧。
🍑 鸡尾酒过程
鸡尾酒排序是什么样子呢?让我们来看一看详细过程:
第一轮(和冒泡排序一样,8和1交换)
第二轮
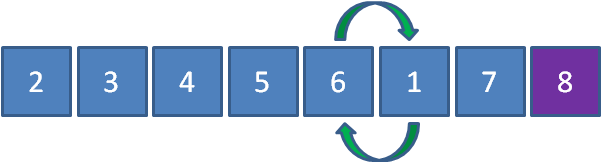
此时开始不一样了,我们反过来从右往左比较和交换:
8已经处于有序区,我们忽略掉8,让1和7比较。元素1小于7,所以1和7交换位置:
接下来1和6比较,元素1小于6,所以1和6交换位置:
接下来1和5比较,元素1小于5,所以1和5交换位置:
接下来1和4交换,1和3交换,1和2交换,最终成为了下面的结果:
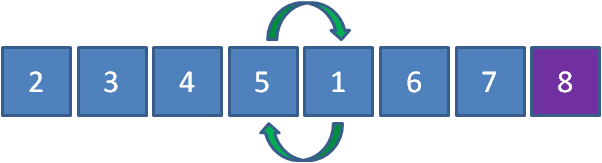
第三轮
虽然已经有序,但是流程并没有结束;
1和2比较,位置不变;2和3比较,位置不变;3和4比较,位置不变…6和7比较,位置不变;
没有元素位置交换,证明已经有序,排序结束。
这就是鸡尾酒排序的思路。
排序过程就像大摆锤一样,第一轮从左到右,第二轮从右到左,第三轮再从左到右…
3. 动图演示
我们先来看个「鸡尾酒排序」的动图吧
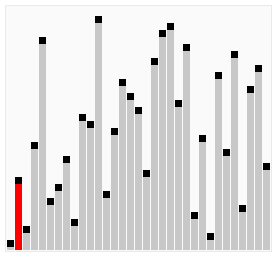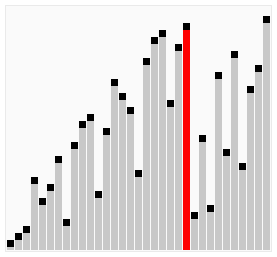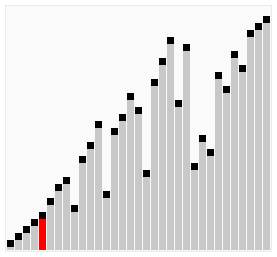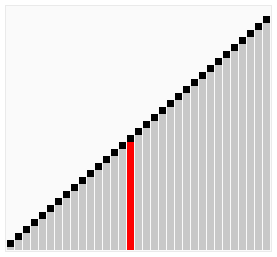
刚刚的「鸡尾酒排序」过程,我们也可以用动图演示👇
第一轮操作( 8 和 1 交换 )
第二轮操作 ( 从序列右边开始遍历 )
第三轮操作 ( 从左向右比较和交换 )
4. 代码实现
📃 代码示例
voidCocktail_Sort(int arr[],int sz){int tmp =0;int left =0;int right = sz -1;for(int i =0; i < sz /2; i++){//有序标记,每一轮的初始是trueint flag =1;//奇数轮,从左向右比较和交换for(int j =0; j < sz - i -1; j++){if(arr[j]> arr[j +1]){
tmp = arr[j];
arr[j]= arr[j +1];
arr[j +1]= tmp;//有元素交换,所以不是有序,标记变为0
flag =0;}}if(flag)break;//偶数轮之前,重新标记为1
flag =1;//偶数轮,从右向左比较和交换for(int j = sz - i -1; j > i; j--){if(arr[j]< arr[j -1]){
tmp = arr[j];
arr[j]= arr[j -1];
arr[j -1]= tmp;//有元素交换,所以不是有序,标记变为0
flag =0;}}if(flag)break;}}voidCocktail_Show(int arr[],int sz){int i =0;for(i =0; i < sz; i++){printf("%d ", arr[i]);}printf("\n");}intmain(){int arr[]={2,3,4,5,6,7,8,1};int sz =sizeof(arr)/sizeof(int);printf("排序前:");Cocktail_Show(arr, sz);//打印排序函数Cocktail_Sort(arr, sz);//排序函数printf("排序后:");Cocktail_Show(arr, sz);return0;}
这段代码是鸡尾酒排序的原始实现。
代码外层的大循环控制着所有排序回合,大循环内包含两个小循环;
第一个循环从左向右比较并交换元素,第二个循环从右向左比较并交换元素。
5. 代码优化
上次介绍冒泡排序的时候,有一种针对有序区间的优化,那么我们的鸡尾酒排序也可以根据这个思路来进行优化;
让我们来回顾一下冒泡排序针对有序区的优化思路:
原始的冒泡排序,有序区的长度和排序的轮数是相等的。
比如第一轮排序过后的有序区长度是1,第二轮排序过后的有序区长度是2 …
要想优化,我们可以在每一轮排序的最后,记录下最后一次元素交换的位置,那个位置也就是无序数列的边界,再往后就是有序区了。
对于单向的冒泡排序,我们需要设置一个边界值;
对于双向的鸡尾酒排序,我们需要设置两个边界值。请看代码:
voidCocktail_Sort(int arr[],int sz){int tmp =0;//无序数列的左边界,每次比较只需要比到这里为止int leftBorder =0;//无序数列的右边界,每次比较只需要比到这里为止int rightBorder = sz -1;//记录右侧最后一次交换的位置int lastRightExchange =0;//记录左侧最后一次交换的位置int lastLeftExchange =0;for(int i =0; i < sz /2; i++){//有序标记,每一轮的初始是trueint flag =1;//奇数轮,从左向右比较和交换for(int j = leftBorder; j < rightBorder; j++){if(arr[j]> arr[j +1]){
tmp = arr[j];
arr[j]= arr[j +1];
arr[j +1]= tmp;//有元素交换,所以不是有序,标记变为0
flag =0;
lastRightExchange = j;}}
rightBorder = lastRightExchange;if(flag)break;//偶数轮之前,重新标记为1
flag =1;//偶数轮,从右向左比较和交换for(int j = rightBorder; j > leftBorder; j--){if(arr[j]< arr[j -1]){
tmp = arr[j];
arr[j]= arr[j -1];
arr[j -1]= tmp;//有元素交换,所以不是有序,标记变为0
flag =0;
lastLeftExchange = j;}}
leftBorder = lastLeftExchange;if(flag)break;}}
代码解释👇
代码中使用了左右两个边界值,
rightSortBorder代表右边界,
leftSortBorder代表左边界。
在比较和交换元素时,奇数轮从
leftSortBorder遍历到
rightSortBorder位置;
偶数轮从
rightSortBorder遍历到
leftSortBorder位置。
6. 特性总结
时间复杂度:同冒泡排序,为
O ( n ² ) O(n²) O(n²)空间复杂度:同冒泡排序,为
O ( 1 ) O(1) O(1)优点:能够在特定的条件下,减少排序的回合数;
缺点:代码量几乎扩大了一倍;
适用场景:大部分元素已经是有序的情况下,使用「鸡尾酒排序」会更好;
总结
🤗作者水平有限,如有总结不对的地方,欢迎留言或者私信!
💕如果你觉得这篇文章还不错的话,那么点赞👍、评论💬、收藏🤞就是对我最大的支持!
🌟你知道的越多,你不知道越多,我们下期见!
版权归原作者 飞向星的客机 所有, 如有侵权,请联系我们删除。