灰色预测GM(1,1)模型

简介

在这里，灰色的意思是系统的信息只有一部分，不完整，与之类似概念还有白色和黑色。

灰色预测模型是通过少量的、不完全的信息，建立数学模型做出预测的一种预测方法。

其预测对象要求数据具有准指数规律，并且数据非负。

灰色预测模型可用GM(m,n)表示，m代表阶数，n代表预测对象的个数。

灰色预测模型适用于年份数据预测，且期数较少的情况。如果期数较多或者包含季度数据，采用时间序列分析进行预测。

数学模型

记原数据序列为

对原数据序列累加得到一次累计序列，1-AGO，记为

得到紧邻均值生成序列

称方程为GM(1,1)模型的基本形式，其中b为灰作用量，-a为发展系数。发展系数越小越好

下面引入矩阵的形式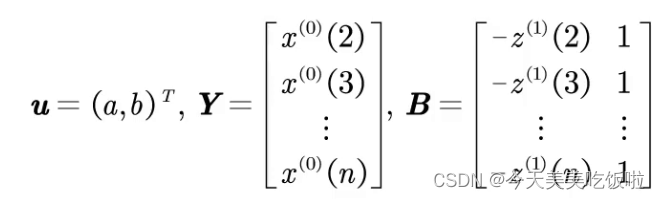

则GM(1,1)的数学模型可用矩阵形式表示为

利用最小二乘法得到参数a,b的估计值为

进而可以得到预测公式

分析步骤

对数据进行准指数规律检验

定义级比

如果级比序列均在区间(1,1.5)之间，则称一次累加序列具有准指数规律

注意到级比，定义原始序列的光滑比，显然光滑比逐渐趋于0，故只需要保证光滑比小于0.5，即通过准指数规律检验。

但实际建模中，不必要求原始序列的光滑比小于0.5的占比，该占比越大越好。

对预测效果进行评价

拟合程度检验

定义相对误差

定义平均误差

如果平均误差小于0.2，则认为GM(1,1)对原始数据的拟合效果一般

级比偏差检验

定义级比偏差

定义平均级比偏差

如果平均级比偏差小于0.2，则认为GM(1,1)对原始数据的拟合效果一般

GM(1,1)模型拓展

全数据GM(1,1)模型，利用原始变量的所有数据

部分数据GM(1,1)模型，只利用原始变量的后部分数据

新信息GM(1,1)模型，预测出的数据作为原始变量数据，递推求得预测数据

新陈代谢GM(1,1)模型，预测出的数作为原始变量数据，同时去掉最老的数据，递推求得预测数据

在实际的建模中，通常在全数据，新信息和新陈代谢3个模型中择优应用。

MATLAB源码

全数据GM(1,1)

function [result,x0_hat,error,eta] = my_GM11(x0,num)
    %%MY_GM11 使用传统GM11对数据进行预测分析
    %%输入参数：
    %   x0:预测原始数据,必须为列向量
    %   num：往后预测的数据个数\
    %%输出参数：
    %   result：预测值
    %   x0_hat：拟合值
    %   relative_error：相对误差
    %   eta：级比偏差
    %% 求解发展系数以及灰作用量
    n=length(x0);
    x1=cumsum(x0);%1-AGO
    z1=1/2*(x1(1:end-1)+x1(2:end));%紧邻均值序列
    Y=x0(2:end);
    B=[-1*z1 ones(length(z1),1)];
    u=inv(B'*B)*B'*Y;
    a=u(1);
    b=u(2);
    %disp('发展系数为',num2str(-a),+'灰作用量是',num2str(b))
    %% 计算拟合值
    x0_hat=zeros(n,1);x0_hat(1)=x0(1);
    for i=1:n-1
        x0_hat(i+1)=(1-exp(a))*(x0(1)-b/a)*exp(-a*i);
    end
    %% 计算预测值
    result=zeros(num,1);%预测值向量
    for i=1:num
        result(i)=(1-exp(a))*(x0(1)-b/a)*exp(-a*(i+n-1));
    end

    %% 输出
    error=abs(x0(2:end)-x0_hat(2:end))./x0(2:end);
    %级比偏差检验
    sigma=x1(2:end)./x1(1:end-1);%级比偏差
    eta=abs(1-(1-0.5*a)/(1+0.5*a))*(1./sigma);
end

新信息GM(1,1)

function [result,x0_hat,bar_error,bar_eta] = my_New_GM11(x0,num)
%MY_NEW_GM11 此处显示有关此函数的摘要
%   此处显示详细说明
    % 参数与my_GM11类似
    result=zeros(num,1);
    for i=1:num
        result(i)=my_GM11(x0,1);
        x0=[x0;result(i)];
    end
end

新陈代谢GM(1,1)

function [result,x0_hat,bar_error,bar_eta] = my_Metabo_GM11(x0,num)
%MY_METABO_GM11 此处显示有关此函数的摘要
%   此处显示详细说明
    result=zeros(num,1);
    for i=1:num
        result(i)=my_GM11(x0,1);
        x0(1)=[];
        x0=[x0;result(i)];
    end
end

应用三种灰色预测模型对数据集进行训练测试

%% 
clc,clear all, close all
%% 输入原始数据并作出时间序列图
data=readmatrix("课后作业：棉花产量预测.xlsx");
data(1,:)=[];
data(end-2:end,:)=[];
year=data(:,1);
x0=data(:,2);
n=length(x0);
figure(1)
plot(year,x0,'o-','LineWidth',1.5);grid on;
xlabel('年份')
ylabel('棉花产量')
%% 判断数据序列是否非负
Error=x0>zeros(length(x0),1);
if Error == ones(length(Error),1)
    disp('原始数据是非负序列，可进行灰色预测')
else
    disp('原始数据不是非负序列，不可以将进行灰色预测')
end
%% 进行准指数规律检验
x1=cumsum(x0);%一次累加序列1——AGO序列
rho=x0(2:end)./x1(1:end-1);
%画出原始序列光滑比
figure(2)
plot(year(2:end),rho,'o-','LineWidth',1.5);grid on;hold on
plot(year(2:end),0.5*ones(length(year)-1,1),'-','LineWidth',1.5);
set(gca,'xtick',year(2:1:end));
legend('光滑度','临界线')
disp(strcat('指标1：光滑比小于0.5的数据占比为',num2str(100*sum(rho<0.5)/(length(year)-1)),'%'))
disp(strcat('指标2：除去前两个时期外，光滑比小于0.5的数据占比为',num2str(100*sum(rho(3:end)<0.5)/(length(year)-3)),'%'))

%% 利用试验组、训练徐，进行传统灰色预测，新信息灰色预测以及新陈代谢灰色预测
testnum=0.25*n;
testnum=round(testnum);%测试数据个数
train_x0=x0(1:end-testnum);%测试数据
test_x0=x0(end-testnum+1:end);%训练数据
result1=my_GM11(train_x0,testnum);%传统GM11
result2=my_New_GM11(train_x0,testnum);%新信息GM11
result3=my_Metabo_GM11(train_x0,testnum);%新陈代谢GM11

%%计算误差平方和SSE
SSE1=sum((test_x0-result1).^2);
SSE2=sum((test_x0-result2).^2);
SSE3=sum((test_x0-result3).^2);
SSE=[SSE1 SSE2 SSE3];
model=find(SSE==min(SSE),1);
disp(strcat('训练结果表明，模型',num2str(model),'结果更好'))
%%画出测试结果图
test_year=year(end-testnum+1:end);
figure(3)
plot(test_year,test_x0,'o-','LineWidth',1.5);grid on;hold on;
plot(test_year,result1,'*-','LineWidth',1.5);grid on; hold on;
plot(test_year,result2,'+-','LineWidth',1.5);grid on;hold on;
plot(test_year,result3,'x-','LineWidth',1.5);grid on;hold on;
legend('原始数据','完全GM11结果','新信息GM11结果','新陈代谢GM11结果')
xlabel('年份')
ylabel('产量')
%% 使用新陈代谢模型对其进行灰色预测
predict_num=4;
[result,x0_hat,error,eta]=my_GM11(x0,predict_num);%使用新陈代谢GM11预测4期
if(model==2)
    result=my_New_GM11(x0,4);
end
if(model==3)
    result=my_Metabo_GM11(x0,4);
end
%% 绘制出相对残差以及级比偏差图
figure(4)
subplot(2,1,1)
plot(year(2:end),error,'*-','LineWidth',1.5);
legend('相对误差')
subplot(2,1,2)
plot(year(2:end),eta,'o-','LineWidth',1.5);
legend('相对级比偏差')
%% 对灰色预测模型进行评估
eta_bar=mean(eta);
if(eta<0.1)
    disp('拟合结果非常不错')
elseif eta<0.2
    disp('拟合结果效果一般')
else
    disp('拟合效果不太好' )
end
%% 绘制最终的预测曲线
figure(5)
plot(year,x0,'o-','LineWidth',1.5);hold on;
plot(year,x0_hat,'-*m','LineWidth',1.5);hold on;
plot(year(end)+1:year(end)+predict_num,result,'-*b','LineWidth',1.5);hold on;
grid on;
legend('原始数据','拟合数据','预测数据');
set(gca,'xtick',[year(1):1:year(end)+predict_num])  % 设置x轴横坐标的间隔为1
xlabel('年份');  ylabel('排污总量');  % 给坐标轴加上标签