0
0

扩散模型原理+DDPM案例代码解析

扩散模型原理+代码解析

一、 数学基础

扩散模型和一般的机器学习的神经网络不太一样！一般的神经网络旨在构造一个网络模型来拟合输入数据与希望得到的输出结果，可以把一般的神经网络当作一个黑盒，这个黑盒通过训练使其输入数据后就可以得到我们想要的结果。而扩散模型包含了大量的统计学和数学相关的知识，我愿把它看作是数学和AI完美结合的产物！由于扩散模型相较于普通的深度学习模型，数学难度大很多，因此学习扩散模型有必要复习（预习）一下相关的数学知识。

1.1 一般的条件概率形式

p(降温/下雨)=0.9 : 表示的意思是在“下雨”的条件下，会“降温”的概率为0.9

p(x∣y)= p(y)p(x,y)， p(x,y)=p(x∣y)p(y)=p(y∣x)p(x)

​P(x,y,z)=P(z∣y,x)P(y,x)=P(z∣y,x)P(y∣x)P(x)

P(y,z∣x)= P(x)P(x,y,z) =P(y∣x)P(z∣x,y)
​

1.2 马尔可夫链条件概率形式

马尔科夫链指的是当前状态的概率只与上一个时刻有关，例如有A->B->C满足马尔可夫关系​
，则有：

​P(x,y,z)=P(z∣y,x)P(y,x)=P(z∣y)P(y∣x)P(x)

P(y,z∣x)=P(y∣x)P(z∣y)

1.3 先验概率和后验概率

在介绍先验概率之前我们先来复习一下全概率公式。
​在这里插入图片描述
可以看出，全概率公式是“由因推果”的思想，当知道某件事的原因后，推断由某个原因导致这件事发生的概率为多少。

先验概率（prior probability）：指根据以往经验和分析。在实验或采样前就可以得到的概率。它往往作为“由因求果”问题中的“因”出现。

在介绍后验概率之前我们先来复习一下贝叶斯公式。
在这里插入图片描述
我们可以发现贝叶斯公式就是一种“由果求因”的思想，当知道某系列些事情的结果后，我们可以根据这类事情推断出发这类事情是某种原因的概率。

后验概率（posterior probability）：指某件事已经发生，想要计算这件事发生的原因是由某个因素引起的概率。指在得到“结果”的信息后重新修正的概率, 是“执果寻因”问题中的“因”。

我们举个例子来更好理解先验、后验概率。

假设我们现在有两个盒子，分别为红色和蓝色。在红色盒子中放着2个苹果和6个橙子，在蓝色盒子中放着1个橙子和3个苹果，如下图所示：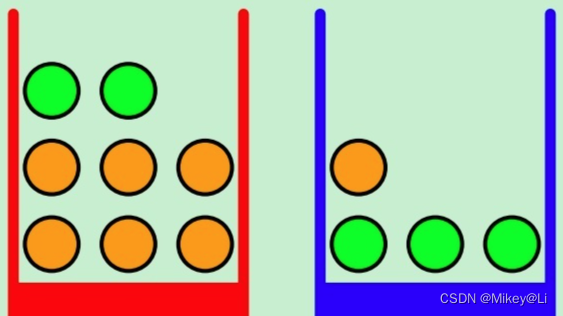
在这里插入图片描述
图中绿色表示苹果，橙色代表橙子。

假设我们每次实验的时候会随机从某个盒子里挑出一个水果，

随机变量B（box）表示挑出的是哪个盒子，并且P(B=blue) = 0.6（蓝色盒子被选中的概率），P(B=red) = 0.4（红色盒子被选中的概率）。

随机变量F（fruit）表示挑中的是哪种水果，F的取值为"a (apple)“和"o (orange)”。

现在假设我们已经得知某次实验中挑出的水果是orange，那么这个orange是从红色盒子里挑出的概率是多大呢？依据贝叶斯公式有：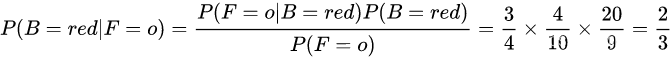
在这里插入图片描述
P(F=o)的概率是根据全概率公式算出来的，

P(F=o)=P(B=blue)* P(F=o|B=blue)+P(B=red) P(F=o|B=red)=0.61/4+0.4*3/4=9/20

同时，由概率的加法规则我们可以得到：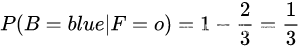
在这里插入图片描述
在上面的计算过程中，我们将P(B=red)或者说P(B)称为先验概率（prior probability），因为我们在得到F是“a”或者“o”之前，就可以得到P(B)。
同理，将P(B=red|F=o)和P(B=blue|F=o)称为后验概率，因为我们在完整的一次实验之后也就是得到了F的具体取值之后才能得到这个概率。

1.4 重参数化技巧

若希望从高斯分布N (μ,σ) 中采样，可以先从标准正态分布N (0,I)中采样出z 再得到σ ∗ z + μ。这样做的好处是将随机性转移到了z 这个常量上，而σ则是仿射变换网络的一部分。

1.5 KL散度公式

对于两个单一变量的高斯分布 p ​和 q ​而言，它们的KL散度为: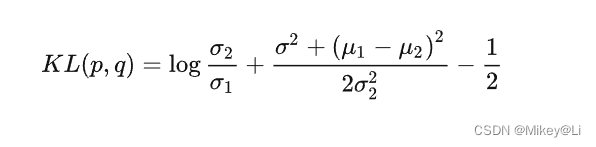
在这里插入图片描述

二、扩散模型的整体逻辑（以DDPM为例）

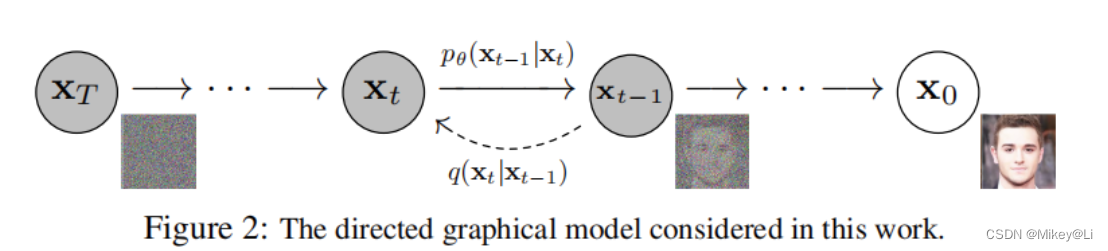
在这里插入图片描述
如上图所示。DDPM模型主要分为两个过程：forward加噪过程（从右往左）和reverse去噪过程（从左往右）。加噪过程意思是指向数据集的真实图片中逐步加入高斯噪声，而去噪过程是指对加了噪声的图片逐步去噪，从而还原出真实图片。加噪过程满足一定的数学规律，而去噪过程则采用神经网络来学习。这么一来，神经网络就可以从一堆杂乱无章的噪声图片中生成真实图片了。

2.1 Diffusion扩散过程（Forward加噪过程）

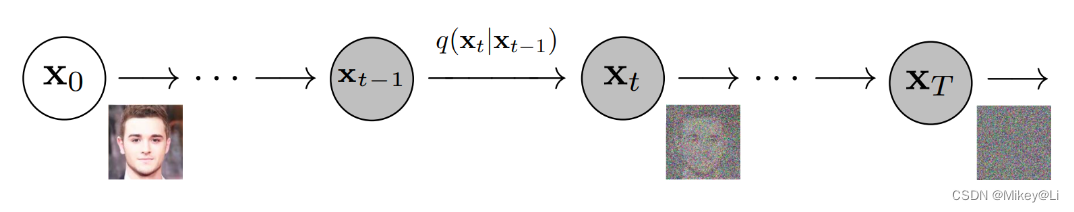
在这里插入图片描述

这里Forward加噪过程是一个马尔科夫链过程，我们可以看到最终通过不断的加入噪声，原始的图片变成了一个完全混乱的图片，这个完全混乱的图片就可以当成一个随机生成的噪声图片。

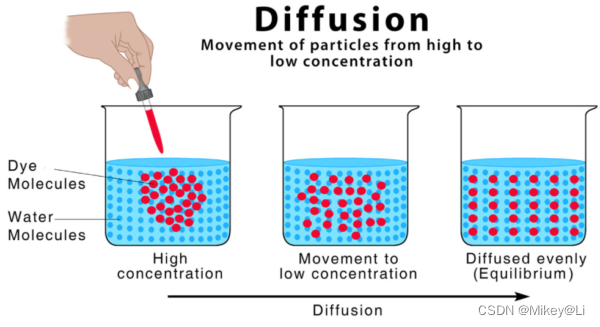
扩散（Diffusion）在热力学中指细小颗粒从高密度区域扩散至低密度区域，在统计领域，扩散则指将复杂的分布转换为一个简单的分布的过程。扩散模型为什么能够起作用是因为它的一个关键性的性质：平稳性。一个概率分布如果随时间变化，那么在马尔可夫链的作用下，它一定会趋于某种平稳分布（例如高斯分布）。只要终止时间足够长，概率分布就会趋近于这个平稳分布。

马尔可夫链每一步的转移概率，本质上都是在加噪声。这就是扩散模型中“扩散”的由来：噪声在马尔可夫链演化的过程中，逐渐进入diffusion体系。随着时间的推移，加入的噪声（加入的溶质）越来越少，而体系中的噪声（这个时刻前的所有溶质）逐渐在diffussion体系中扩散，直至均匀。

在这里插入图片描述
Diffusion模型定义了一个概率分布转换模型T(注意：这不是"t ∈ { 1 , 2 , 3… T }"中的T)，能将原始数据x0构成的复杂分布qcomplex 转换为一个简单的已知参数的先验分布pprior: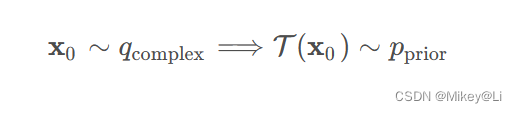
在这里插入图片描述
具体来说，Diffusion模型提出可以用马尔科夫链(Markov Chain)来构造T，即定义一系列条件概率分布q(x t∣ xt-1 ) t ∈ { 1 , 2 , 3… T } , 将x 0 依次转换为x 1 、x 2 、x 3 …x T
,希望当T 足够大时：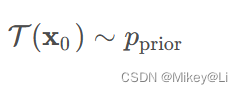
在这里插入图片描述
为了简洁和有效，此处的pprior选择高斯分布,因此整个前向扩散过程可以被看作是，在T步内，不断添加少量的高斯噪声到样本中。
具体来说，在马尔科夫链的每一步，我们向 xt-1添加方差为βt的高斯噪声，产生一个新的隐变量
xt，其分布为 q(x t∣ xt-1 ) 。这个扩散过程可以表述如下：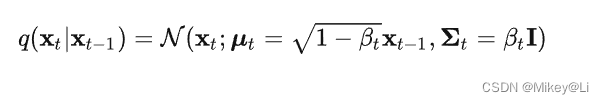
在这里插入图片描述

由于我们处于多维情况下，I是单位矩阵，表明每个维度有相同的标准偏差 βt。注意到， q(x t∣ xt-1 ) 是一个正态分布，其均值是 μ t，方差为 ∑ t，其中 ∑是一个对角矩阵的方差（这里就是 βt ）。

因此，我们可以自 x 0 到 x T 以一种可操作的方式来近似输入。在数学上，这种后验概率定义如下：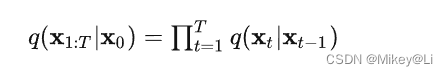
在这里插入图片描述
其中， x 1 :T 意味着我们从时间 1 到 T 重复应用 q(x t∣ xt-1 ) 。

这种累乘的方式过于繁琐，利用重参数化技巧，可以得到：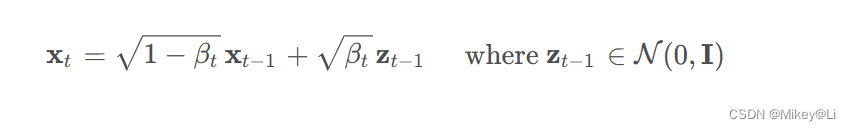
在这里插入图片描述
在这里插入图片描述
β不断增大，论文中是0.0001~0.002，所以之后α越来越小。则：当前向时刻越往后，噪音影响的权重越来越大，z是服从高斯分布的噪音，当 t 趋近于正无穷时， x t等同于各向同性的高斯分布。
这样我们就可以直接得到任意时刻的 x t 。

2.2 逆向过程（reverse去噪过程）

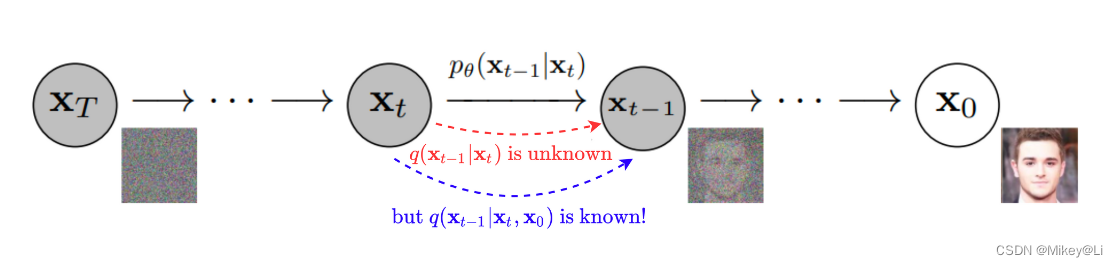
在这里插入图片描述
Diffusion Model的逆向过程就是与正向Forward加噪过程相反不断去除图像中的噪声的过程。不幸的是， q(x t∣ xt-1 ) 虽然知道但是 q(x t-1∣ xt ) 却是未知的。但有相关研究表明：连续扩散过程的逆转具有与正向过程相同的分布形式。即，即当扩散率βt足够小，扩散次数足够多时，离散扩散过程接近于连续扩散过程 q(x t∣ xt-1 ) 的分布形式同 q(x t-1∣ xt ) 一致，同样是高斯分布。
尽管如此，我们依然不能够直接得到 q(x t-1∣ xt )，因此我们就需要学习一个网络模型 p(x t-1∣ xt)拟合 q(x t-1∣ xt )：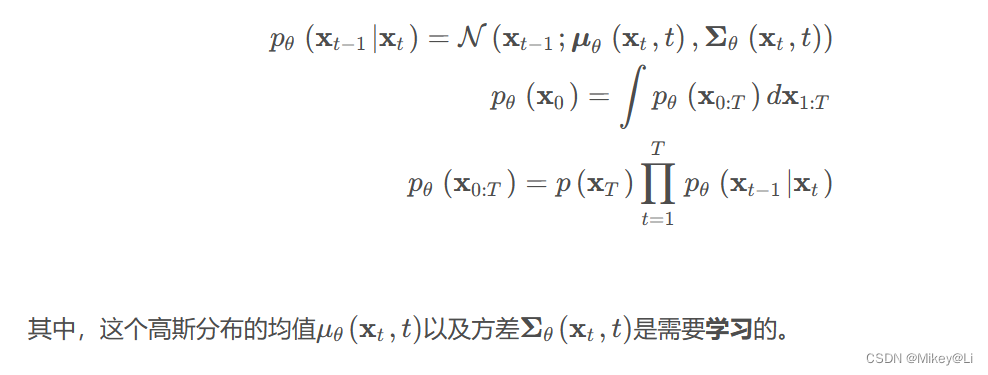
在这里插入图片描述
在DDPM中不学习方差，方差设置为βt。
这样，逆向过程中高斯的后验概率定义为：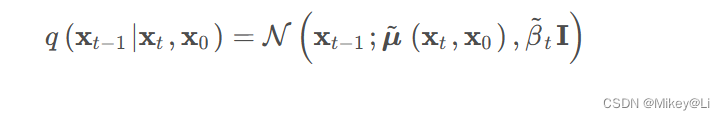
在这里插入图片描述
使用贝叶斯公式可以得到：
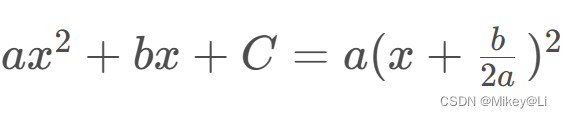
在这里插入图片描述
利用公式:
在这里插入图片描述
将上面由贝叶斯公式得到的结果凑成高斯分布概率密度的形式：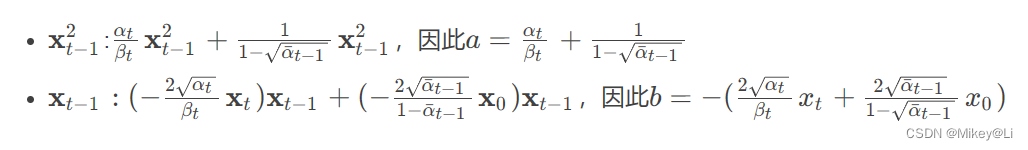
在这里插入图片描述
因此，我们可以得到q(x t-1∣ xt ，x 0)的高斯概率密度表示为：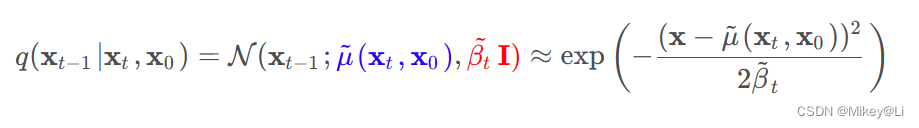
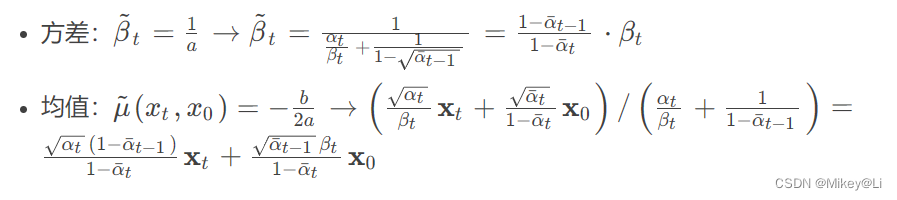
在这里插入图片描述
在这里插入图片描述
用x t替换x 0得：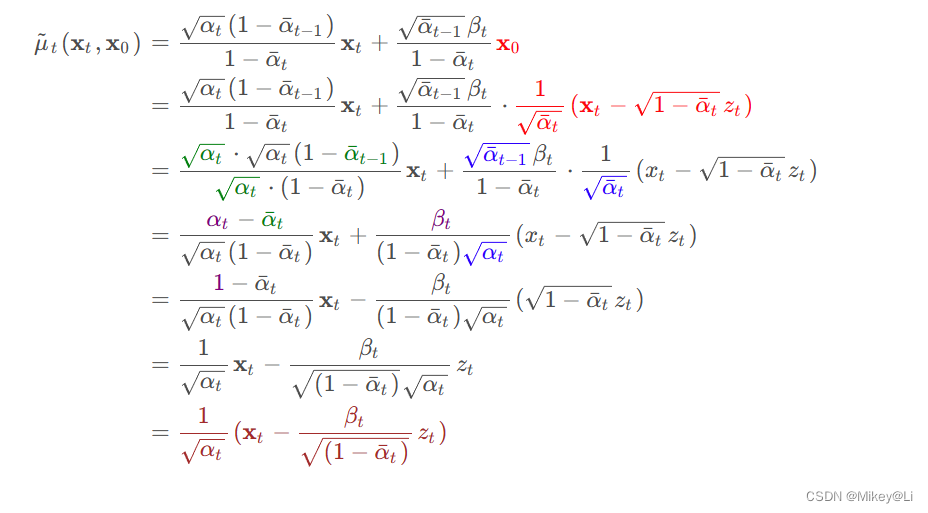
在这里插入图片描述
到此，我们在逆向过程中的目标就变成了拉近以下两个高斯分布的距离，这可以通过计算两个分布的KL散度实现，其中q(x t-1∣ xt ，x 0)的均值和方差都是已知的：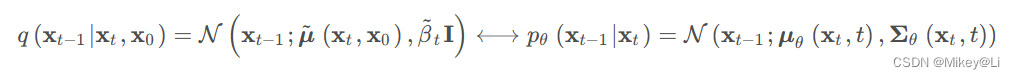
在这里插入图片描述
这就是我们训练网络的损失函数。

三、训练过程和采样过程

我们重新梳理一下扩散模型的整个流程。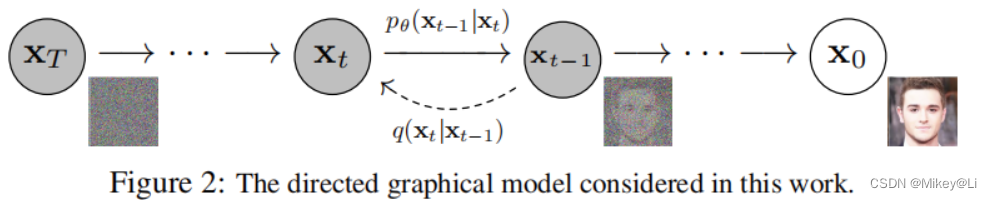
在这里插入图片描述
前向传播过程（q过程）：从x0开始不断加入噪声到 xt， xt只是一个带有噪声的图片，再逐渐加入更多噪声，到 xT的时候图片已经完全变成一个噪声图片了。
逆向过程（p过程）：在一张完全混乱的噪声图片当中不断拿去刚刚加入的噪声，让其变得不混乱，逐步更加接近真实图片，就可以得到最开始的图片。

前向过程是一个完全的马尔科夫链加入噪声过程实通过固定计算完成的，逆向过程里面如何预测噪声就成了我们的关键需求，人是算不出来的，所以我们需要借助网络来帮忙。

3.1 训练过程

我们在逆向降噪过程中由于没办法得到q(x t-1∣ xt )，因此定义了一个 需要学习的模型p(x t-1∣ xt ) 来对其进行近似，并且在训练阶段我们可以利用后验q(x t-1∣ xt ，x 0)来对p进行优化（就是计算损失不断训练的过程）。
那么，要怎么优化这个p呢？即如何训练模型预测到靠谱的均值和方差根据分布进行计算呢？
我们可以最大化模型预测分布的对数似然，优化模型真实分布和预测分布的交叉熵，优化 x0 ~ q(x 0)下的 Pθ（x0）交叉熵：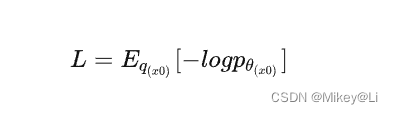
在这里插入图片描述
使用变分下限优化负对数似然，因为KL散度非负：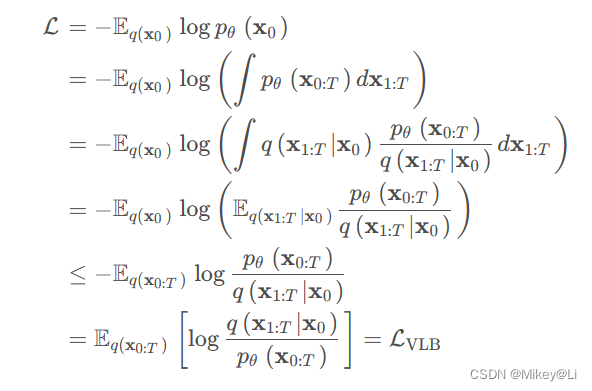
在这里插入图片描述

上式中q (x0)是真实的数据分布，而Pθ（x0）是模型。

为了最小化这个损失，可以将其转化为最小化其上界LVLB:
在这里插入图片描述
由于前向q没有可学习参数，而xT则是纯高斯噪声，LT可以当做常量忽略。因此我们只要研究L0和Lt(t和t-1其实意思是一样的）。
Lt可以看作是拉近2个高斯分布q(x t-1∣ xt ，x 0)和p(x t-1∣ xt ) ，可以根据多元高斯分布的KL散度求解：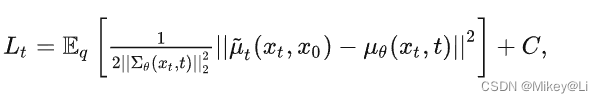
在这里插入图片描述
把前面得到的公式：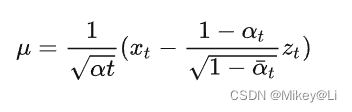
在这里插入图片描述
代入得：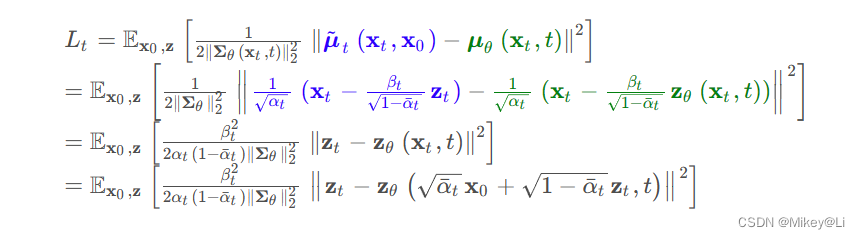
在这里插入图片描述
我们可以看出，扩散模型训练的核心是学习真实噪声 zt和预测噪声z θ的均方误差MSE, DDPM (Ho et al 2020)使用了不带权重项的简化损失, 使得训练更加稳定：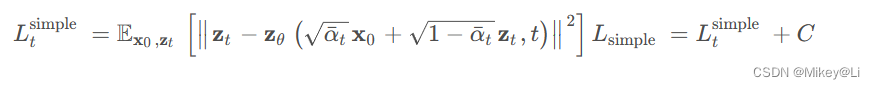
在这里插入图片描述
其中C是一个常数。
对于L0: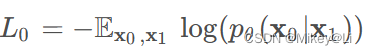
在这里插入图片描述
因为：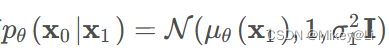
在这里插入图片描述
实际上L0是一个多元高斯分布的负对数似然期望，即其熵：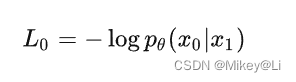
在这里插入图片描述
多元高斯分布的熵仅与其协方差有关，即L0仅与σ1^2 I有关，L0是个常数。

综上，扩散模型（DDPM）的训练过程可以看做是最小化预测噪声和真实采样的ϵ之间的距离的过程。
DDPM论文里面训练过程的伪代码如下：
在这里插入图片描述
可以理解为：
在这里插入图片描述
重复这一过程直到网络收敛。

3.2 采样过程

DDPM论文中对采样过程的描述：
在这里插入图片描述
因为我们通过训练已经得到了一个用于拟合 q(x t-1∣ xt )的网络p(x t-1∣ xt)，因此我们可以从 xT一步步得到 x0。具体的步骤可以为：
在这里插入图片描述

3.3 模型训练的一些细节

3.3.1 网络的选择

扩散模型的网络的输入和输出都是同等规格的，因此理论上只要网络的input的规格和output规格一样就可以。比如你可以选择Unet作为拟合的网络：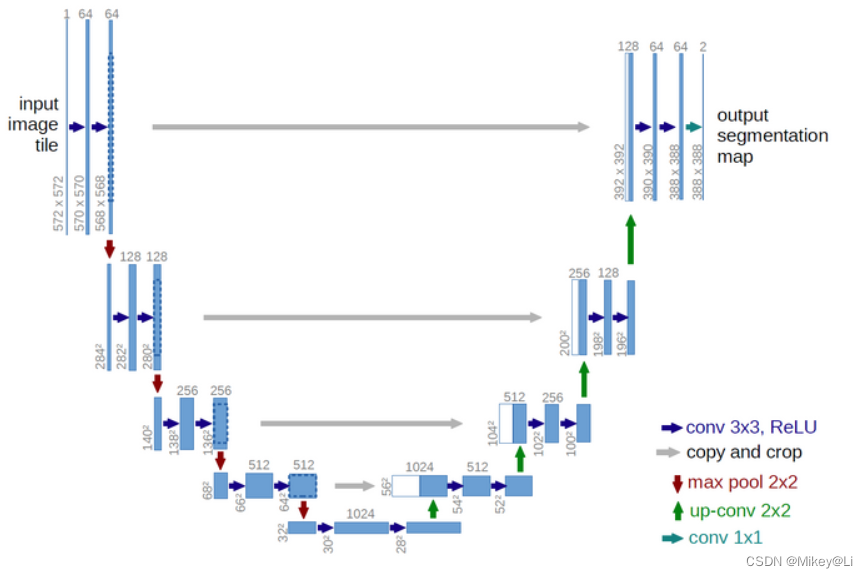
在这里插入图片描述

3.3.2 一些超参数的选择

在前向传播的过程中，我们不知道噪声到底要添加到什么时候才合适，每次添加噪声的方差怎么设置也是很重要。这些都需要不断的尝试调优才能得到。
DDPM中T设置为1000，βt被设置为从β1 = 0.0001到βT=0.02线性增加。当然别的扩散模型也有不同的策略，只要能够调试网络到最好就是最好的方法。不同任务不同的网络策略可能也会不同。

四、DDPM案例代码实现

为了更好的掌握扩散模型的工作过程，我参考网上的代码一步步编写调试了一个简单扩散模型案例-
DDPM S_curve
在这里插入图片描述

4.1 数据集准备

在这里插入图片描述
这里需要注意的是，这里的整个数据集就是上面可视化的这张图片中的点，一共有10000个数据，每个数据就是构成上面这张图中S的一个个点，一共有10000个点，这些点满足这是“s”形的分布。
构建数据集的代码：

import numpy as np
from sklearn.datasets import make_s_curve
import torch

s_curve,_ = make_s_curve(10**4, noise=0.1)
s_curve = s_curve[:,[0,2]]/10.0#  得到的是一个三维的点我们只需要二维的
device ='cuda'if torch.cuda.is_available()else'cpu'
dataset = torch.Tensor(s_curve).float().to(device)

对数据集进行可视化：

data = s_curve.T
fig,ax = plt.subplots()
ax.scatter(*data,color='blue',edgecolor='white');
ax.axis('off')
plt.show()

4.2 前向传播过程

先确定两个超参数β(betas)和T(num_steps),我们T设置为100,β先从（-6,6）取100个数，然后用sigmoid得到100个非线性增加的数。

num_steps =100
betas = torch.linspace(-6,6, num_steps).to(device)
betas = torch.sigmoid(betas)*(0.5e-2-1e-5)+1e-5

提前计算好前向传播公式中需要用到的表达：
在这里插入图片描述

alphas =1-betas

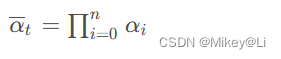
在这里插入图片描述

alphas_prod = torch.cumprod(alphas, dim=0)

αt-1

alphas_prod_p = torch.cat([torch.tensor([1]).float().to(device),alphas_prod[:-1]],0)

在这里插入图片描述

one_minus_alphas_bar_log = torch.log(1- alphas_prod)

在这里插入图片描述

one_minus_alphas_bar_sqrt = torch.sqrt(1- alphas_prod)

根据公式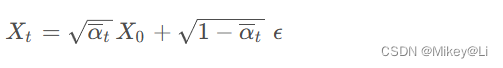
在这里插入图片描述
编写一个可以获得任意时刻t的状态图Xt的函数：

defq_x(x_0,t):
    noise = torch.randn_like(x_0).to(device)#随机获得的一个和x_0一样规格的噪声
    alphas_t = alphas_bar_sqrt[t]
    alphas_1_m_t = one_minus_alphas_bar_sqrt[t]return(alphas_t * x_0 + alphas_1_m_t * noise)#在x[0]的基础上添加噪声

可视化每5步添加噪声后的数据集：

num_shows =20
fig,axs = plt.subplots(2,10,figsize=(28,3))
plt.rc('text',color='black')for i inrange(num_shows):
    j = i//10
    k = i%10
    q_i = q_x(dataset, torch.tensor([i*num_steps//num_shows]).to(device))#生成t时刻的采样数据
    q_i = q_i.to('cpu')
    axs[j,k].scatter(q_i[:,0],q_i[:,1],color='red',edgecolor='white')
    axs[j,k].set_axis_off()
    axs[j,k].set_title('$q(\mathbf{x}_{'+str(i*num_steps//num_shows)+'})$')

在这里插入图片描述
定义损失函数：

defdiffusion_loss_fn(model, x_0, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, n_steps):"""对任意时刻t进行采样计算loss"""
    batch_size = x_0.shape[0]# 对一个batchsize样本生成随机的时刻t
    t = torch.randint(0, n_steps, size=(batch_size //2,)).to(device)
    t = torch.cat([t, n_steps -1- t], dim=0)
    t = t.unsqueeze(-1)# x0的系数
    a = alphas_bar_sqrt[t]# eps的系数
    aml = one_minus_alphas_bar_sqrt[t]# 生成随机噪音eps
    e = torch.randn_like(x_0).to(device)# 构造模型的输入
    x = x_0 * a + e * aml

    # 送入模型，得到t时刻的随机噪声预测值
    output = model(x, t.squeeze(-1))# 与真实噪声一起计算误差，求平均值return(e - output).square().mean()

该损失函数计算的就是网络预测的噪声与真实噪声的损失。x = x_0 * a + e * aml就是公式：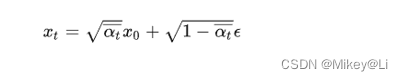
在这里插入图片描述

4.3 逆向过程（模型训练过程）

这里需要定义一个从XT恢复到X0的一个函数：

defp_sample_loop(model,shape,n_steps,betas,one_minus_alphas_bar_sqrt):"""从x[T]恢复x[T-1]、x[T-2]|...x[0]"""
    cur_x = torch.randn(shape).to(device)
    x_seq =[cur_x]for i inreversed(range(n_steps)):
        cur_x = p_sample(model,cur_x,i,betas,one_minus_alphas_bar_sqrt)
        x_seq.append(cur_x)return x_seq

defp_sample(model,x,t,betas,one_minus_alphas_bar_sqrt):"""从x[T]采样t时刻的重构值"""
    t = torch.tensor([t]).to(device)
    coeff = betas[t]/ one_minus_alphas_bar_sqrt[t]
    eps_theta = model(x,t)
    mean =(1/(1-betas[t]).sqrt())*(x-(coeff*eps_theta))
    z = torch.randn_like(x).to(device)
    sigma_t = betas[t].sqrt()
    sample = mean + sigma_t * z
    return(sample)

然后就是定义一个网络模型用于拟合q，这里定义的全是线性层连接的网络：
这里回推运用到了一个公式：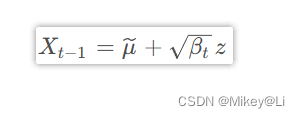
在这里插入图片描述

# 定义拟合的网络classMLPDiffusion(nn.Module):def__init__(self, n_steps, num_units=128):super(MLPDiffusion, self).__init__()

        self.linears = nn.ModuleList([
                nn.Linear(2, num_units),
                nn.ReLU(),
                nn.Linear(num_units, num_units),
                nn.ReLU(),
                nn.Linear(num_units, num_units),
                nn.ReLU(),
                nn.Linear(num_units,2),])
        self.step_embeddings = nn.ModuleList([
                nn.Embedding(n_steps, num_units),
                nn.Embedding(n_steps, num_units),
                nn.Embedding(n_steps, num_units),])defforward(self, x, t):#         x = x_0for idx, embedding_layer inenumerate(self.step_embeddings):
            t_embedding = embedding_layer(t)
            x = self.linears[2* idx](x)
            x += t_embedding
            x = self.linears[2* idx +1](x)

        x = self.linears[-1](x)return x

最后就是常规的网络训练过程，我们的batch_size设置为128，训练4000个轮次，因为网络很简单，我的电脑不到20分钟就训练完了。过程中每100轮次可视化一次。

seed =1234print('Training model...')
batch_size =128
dataloader = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
num_epoch =4000
plt.rc('text',color='blue')

model = MLPDiffusion(num_steps)#输出维度是2，输入是x和step
model = model.cuda()
optimizer = torch.optim.Adam(model.parameters(),lr=1e-3)for t inrange(num_epoch):for idx,batch_x inenumerate(dataloader):
        loss = diffusion_loss_fn(model,batch_x,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,num_steps)
        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_norm_(model.parameters(),1.)
        optimizer.step()if(t%100==0):print(loss)
        x_seq = p_sample_loop(model,dataset.shape,num_steps,betas,one_minus_alphas_bar_sqrt)
        
        x_seq =[item.to('cpu')for item in x_seq]
        fig,axs = plt.subplots(1,10,figsize=(28,3))for i inrange(1,11):
            cur_x = x_seq[i*10].detach()
            axs[i-1].scatter(cur_x[:,0],cur_x[:,1],color='red',edgecolor='white');
            axs[i-1].set_axis_off();
            axs[i-1].set_title('$q(\mathbf{x}_{'+str(i*10)+'})$')

下面展示的是训练过程中的一部分可视化输出：
epoch=0
在这里插入图片描述
epoch=200
在这里插入图片描述
epoch =600
在这里插入图片描述
epoch=1500
在这里插入图片描述
epoch =3000
在这里插入图片描述
epoch = 4000
在这里插入图片描述
参考文献
[1]: https://zhuanlan.zhihu.com/p/415487792
[2]: https://zhuanlan.zhihu.com/p/499206074
[3]: https://blog.csdn.net/weixin_42363544/article/details/127495570
[4]:https://blog.csdn.net/weixin_43850253/article/details/128275723
[5]:Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models[J]. Advances in Neural Information Processing Systems, 2020, 33: 6840-6851.

标签： 机器学习 人工智能 深度学习
本文转载自: https://blog.csdn.net/weixin_46088099/article/details/129753272
版权归原作者 Mikey@Li 所有， 如有侵权，请联系我们删除。
登录后发布评论

“扩散模型原理+DDPM案例代码解析”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

docker 安装 mysql

使用idea和vecode创建vue项目并启动（超详细）

科普文：微服务之SpringBoot性能优化器动态线程池【Dynamic-Tp】特性和源码解读

[实时计算flink]双流JOIN语句

【若依】若依Vue3前端拆解分析--布局分析--index篇

Spring Boot 3.4.0 发行：革新与突破的里程碑

索引（MySQL）

文章导航