
目录
1 分类
图像滤波按图像域可分为两种类型:
- 邻域滤波(Spatial Domain Filter),其本质是数字窗口上的数学运算。一般用于图像平滑、图像锐化、特征提取(如纹理测量、边缘检测)等,邻域滤波使用邻域算子——利用给定像素周围像素值以决定此像素最终输出的一种算子
- **频域滤波(Frequency Domain Filter)**,其本质是对像素频率的修改。一般用于降噪、重采样、图像压缩等。
按图像频率滤除效果主要分为两种类型:
- 低通滤波。滤除原图像的高频成分,即模糊图像边缘与细节。
- 高通滤波。滤除原图像的低频成分,即图像锐化。
导入原图和噪图
import cv2,skimage
import numpy as np
# 原图
srcImg = cv2.imread("test.jpg")
cv2.imshow("src image", srcImg)# 给图像增加高斯噪声
noiseImg = skimage.util.random_noise(srcImg, mode='gaussian')
cv2.imshow("image with noise", noiseImg)


其中噪声可选
gaussian:高斯加性噪声localvar:高斯加性噪声,每点具有特定局部方差poisson: 泊松分布噪声salt:盐噪声,随机用1替换像素pepper:胡椒噪声,随机用0或-1替换像素s&p:椒盐噪声,呈现出黑白杂点
2 邻域滤波
2.1 线性滤波
线性邻域滤波,指像素的输出值取决于输入区域像素的加权和,下面介绍常见的线性滤波算子。
2.1.1 方框滤波
**方框滤波(Box Filter)**,其核函数为:
K
e
r
=
1
α
[
1
1
⋯
1
1
1
⋯
1
⋮
⋮
⋱
⋮
1
1
⋯
1
]
Ker\,\,=\,\,\frac{1}{\alpha}\left[ \begin{matrix} 1& 1& \cdots& 1\\ 1& 1& \cdots& 1\\ \vdots& \vdots& \ddots& \vdots\\ 1& 1& \cdots& 1\\\end{matrix} \right]
Ker=α1⎣⎢⎢⎢⎡11⋮111⋮1⋯⋯⋱⋯11⋮1⎦⎥⎥⎥⎤
其中
α
=
{
1
K
e
r
S
i
z
e
,
N
o
r
m
a
l
i
z
e
=
T
r
u
e
1
,
N
o
r
m
a
l
i
z
e
=
F
a
l
s
e
\alpha =\begin{cases} \frac{1}{KerSize}\,\, , Normalize\,\,=\,\,True\\ 1 , Normalize\,\,=\,\,False\\\end{cases}
α={KerSize1,Normalize=True1,Normalize=False
非归一化的方框滤波用于计算每个像素邻域内的积分特性,比如**密集光流算法(Dense Optical Flow Algorithms)**中用到的图像倒数的协方差矩阵。
归一化的方框滤波则为**均值滤波(Blur)**,即邻域平均法——用一片图像区域各个像素的均值来代替原图像中的各个像素值。均值滤波用于图像平滑,但其在降噪的同时也破坏了图像的边缘细节,从而使图像变得模糊,降噪能力较差。
进行方框滤波
# 方框滤波
boxImg = cv2.boxFilter(noiseImg, ddepth =-1, ksize =(2,2), normalize =False)
cv2.imshow("box Image", boxImg)# 均值滤波
blurImg = cv2.blur(noiseImg,(6,5))
cv2.imshow("blur image", blurImg)
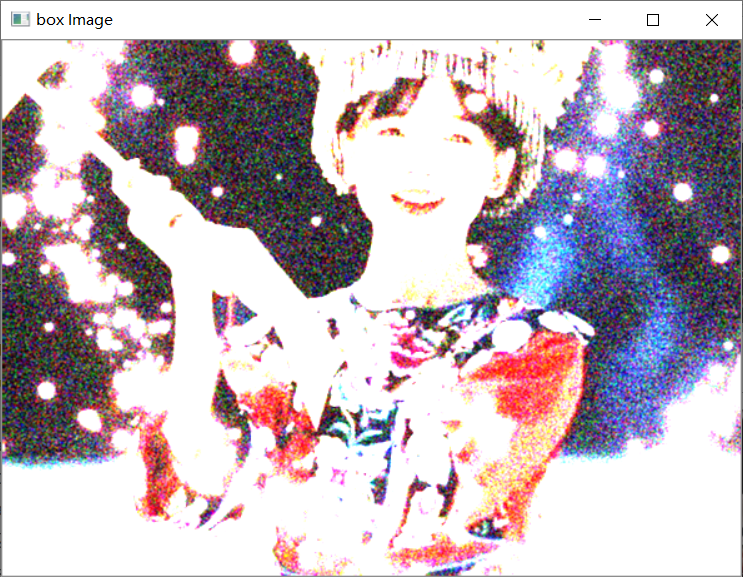

若将方框滤波核设为
(6,5)
且归一化,则效果与均值滤波相同。
2.1.2 高斯滤波
**高斯滤波(Gauss Filter)**基于二维高斯核函数
G
(
x
,
y
,
σ
)
=
1
2
π
σ
2
e
−
x
2
+
y
2
2
σ
2
G\left( x,y,\sigma \right) =\frac{1}{2\pi \sigma ^2}e^{-\frac{x^2+y^2}{2\sigma ^2}}
G(x,y,σ)=2πσ21e−2σ2x2+y2
具有在保持细节的条件下进行噪声滤波的能力,因此广泛应用于图像降噪中,但其效率比均值滤波低。
高斯滤波器有两个特征量:
- 核大小,其决定了图像的平滑范围。理论上,高斯核函数应该无穷大,以达到最佳的平滑效果,但过大的卷积核会导致运算效率骤降。根据高斯函数 3 σ 3\sigma 3σ规则,可以取高斯核大小为 ( 6 σ + 1 ) × ( 6 σ + 1 ) \left( 6\sigma +1 \right) \times \left( 6\sigma +1 \right) (6σ+1)×(6σ+1);
- 离散程度 σ \sigma σ,其决定了对高频成分的抑制程度。 σ \sigma σ越大,像素加权半径越大,平滑程度越强。

# 高斯滤波
gaussImg = cv2.GaussianBlur(noiseImg,(5,5),0)
cv2.namedWindow("gaussain image")
cv2.imshow("gaussain image", gaussImg)

2.2 非线性滤波
虽然线性滤波器易于构造且计算效率高,但有些情况下,使用邻域像素的非线性滤波效果更好。例如,若图像具有椒盐噪声而非高斯噪声,此时对图像高斯滤波并不会去除噪声像素,只是把噪声转换为更为柔和但仍然可见的颗粒。

中值滤波(Median filter)是一种基于排序统计理论的典型非线性滤波技术,核心原理是用像素点邻域灰度值中值代替该像素点的灰度值。中值滤波对脉冲噪声、椒盐噪声尤为有效,且具有边缘保护特性。中值滤波器本质上是数字窗口内的非线性取中值运算,而非线性滤波器的加权运算,因此中值滤波没有卷积核,运算效率仅有线性滤波的1/5左右。
# 原图
srcImg = cv2.imread("test.jpg")
cv2.imshow("src image", srcImg)# 给图像增加椒盐噪声
noiseImg = skimage.util.random_noise(srcImg, mode='s&p')
cv2.imshow("image with noise", noiseImg)
medImg = cv2.medianBlur(np.uint8(noiseImg *255),3)
cv2.namedWindow("median image")
cv2.imshow("median image", medImg)


中值滤波对椒盐噪声效果
3 频域滤波
通过傅里叶变换将图像变换到频域,即可在频域进行图像处理。根据傅里叶变换的对称性以及从低频到高频的排列规则,图像原始频域图像会在四角形成低频分量区,而形成高频中心。通常为了观察方便,变换算法(例如Matlab中的fftshift)会将低频分量移动到图像中心形成低频中心
图像傅里叶变换代码如下
# 傅里叶变换
dft = cv2.dft(np.float32(grayImg), flags = cv2.DFT_COMPLEX_OUTPUT)# 将图像中的低频部分移动到图像的中心
dftShift = np.fft.fftshift(dft)# 计算幅频特性
magnitude =20* np.log(cv2.magnitude(dftShift[:,:,0], dftShift[:,:,1]))
plt.subplot(121), plt.imshow(grayImg, cmap ='gray')
plt.title('原图'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude, cmap ='gray')
plt.title('频谱图'), plt.xticks([]), plt.yticks([])
plt.show()
3.1 低通滤波
# 定义滤波掩码defmask(img, ftype):
crow, ccol =int(img.shape[0]/2),int(img.shape[1]/2)# 求得图像的中心点位置# 低通if ftype =='low':
mask = np.zeros((img.shape[0], img.shape[1],2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30]=1# 高通if ftype =='high':
mask = np.ones((img.shape[0], img.shape[1],2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30]=0return mask
lowImg = dftShift * mask(grayImg,'low')
lowImg = np.fft.ifftshift(lowImg)
lowImg = cv2.idft(lowImg)
lowImg = cv2.magnitude(lowImg[:,:,0], lowImg[:,:,1])

3.2 高通滤波
# 定义滤波掩码defmask(img, ftype):
crow, ccol =int(img.shape[0]/2),int(img.shape[1]/2)# 求得图像的中心点位置# 低通if ftype =='low':
mask = np.zeros((img.shape[0], img.shape[1],2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30]=1# 高通if ftype =='high':
mask = np.ones((img.shape[0], img.shape[1],2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30]=0return mask
highImg = dftShift * mask(grayImg,'high')
highImg = np.fft.ifftshift(highImg)
highImg = cv2.idft(highImg)
highImg = cv2.magnitude(highImg[:,:,0], highImg[:,:,1])

完整代码关注下方公众号回复 CV002 获取
🚀 计算机视觉基础教程说明
章号 内容
0 色彩空间与数字成像
1 计算机几何基础
2 图像增强、滤波、金字塔
3 图像特征提取
4 图像特征描述
5 图像特征匹配
6 立体视觉
7 项目实战
🔥 更多精彩专栏:
- 《机器人原理与技术》
- 《计算机视觉教程》
- 《机器学习》
- 《嵌入式系统》
- 《数值优化方法》
- …
👇配套代码 · 优质体验 · 系统知识 请关注👇
版权归原作者 FrigidWinter 所有, 如有侵权,请联系我们删除。
