LLM自我改进的典型范式是在自生成数据上训练LLM,但是其中的部分数据可能有害,所以应该被过滤掉。但是目前的工作主要采用基于答案正确性的过滤策略,在这篇论文中,证明过滤掉正确但具有高分布偏移程度(DSE)的样本也可以有利于自我改进的结果。
论文的主要贡献如下:
- 提出了一个称为DS权重的指标,借助一个微小的有效集来近似LLM自生成数据的DSE
- 利用DS权重,构建了一个新颖的自我改进框架,称为基于重要性加权的自我改进(IWSI),其中过滤策略同时考虑了答案正确性和DSE
- 实证检验了论文提出方法的有效性,分析了高DSE样本对LLM自我改进的影响,并探讨了DS权重如何与其他过滤标准相互作用
方法论
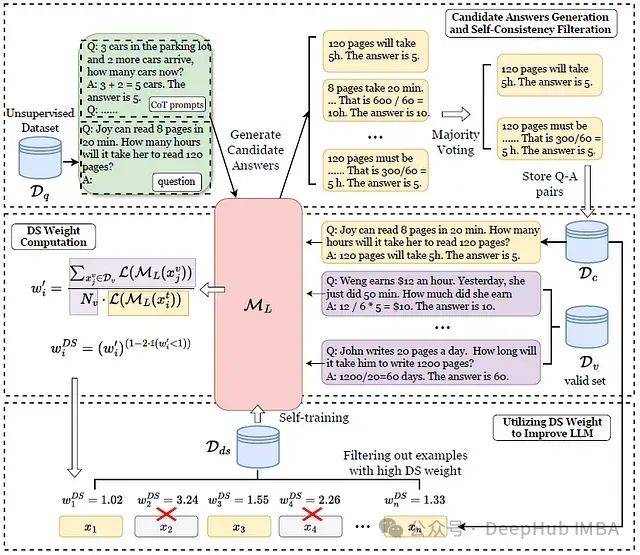
给定一个无监督(仅问题)数据集D𝑞,首先使用预训练的LLM M𝐿使用CoT提示每个问题生成多个候选答案以及推理思路,然后IWSI使用多数投票选择最一致的答案和相应的思路,存储在过滤后的数据集D𝑐中在微小有效集D𝑣的帮助下,IWSI计算D𝑐中每个数据点的DS权重。IWSI通过保留DS权重最低的𝑘%样本将D𝑐过滤成D𝑑𝑠,最后对M𝐿进行自我训练
1、候选答案生成和自一致性过滤
在这个阶段,让预训练的LLM M𝐿为仅包含未标记问题的无监督数据集D𝑞生成候选答案和推理思路,给定一个问题𝑞𝑖 ∈ D𝑞,将少量样本CoT提示与𝑞𝑖连接形成输入文本𝑥𝑖。在温度𝑇 > 0的情况下,让M𝐿采样𝑚个候选答案[𝑎𝑖1 , 𝑎𝑖2 , . . . , 𝑎𝑖𝑚]及其推理思路[𝑟𝑖1 , 𝑟𝑖2 , . . . , 𝑟𝑖𝑚]。然后通过多数投票选择最一致的答案𝑎ˆ𝑖
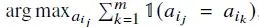
并保留相应的推理思路𝑅𝑖 = {𝑟𝑖 𝑗 |𝑎𝑖 𝑗 = 𝑎ˆ𝑖 , 1 ≤ 𝑗 ≤ 𝑚},通过对D𝑞中的每个问题重复这个过程,构建了一致性过滤后的数据集D𝑐
2、DS权重计算
分布偏移问题表示训练数据和测试数据是从两个不同的分布𝑝𝑡𝑟𝑎𝑖𝑛和𝑝𝑡𝑒𝑠𝑡中抽取的,且𝑝𝑡𝑟𝑎𝑖𝑛 ≠ 𝑝𝑡𝑒𝑠𝑡。分布偏移的一个常见假设是存在一个函数𝑤∗(𝑥),满足:
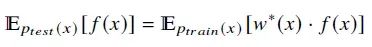
对于x的任何函数,重要性加权方法[3][4]通过两个步骤处理分布偏移:权重估计为𝑤∗(𝑥)找到一个合适的解;加权分类通过将上述等式中的𝑓替换为目标损失函数来训练模型.为简化问题,DIW[5]在有效集的帮助下提供了一个经验替代目标:
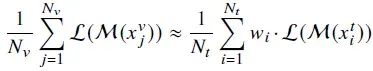
其中𝑁𝑣、𝑁𝑡、𝑥𝑣和𝑥𝑡分别表示有效集的大小、训练集的大小、有效集中的数据和训练集中的数据。M是训练模型,L代表训练损失。
直观理解是,当训练数据分布与有效数据分布相同时,𝑤𝑖 ≡ 1将是上述等式的一个合适解。如果实际𝑤𝑖与1的差异越大,训练分布和有效分布的差异就越大。基于这个想法,首先通过将𝑁𝑡视为1来为𝑥𝑡𝑖设计一个简单的估计𝑤′𝑖:
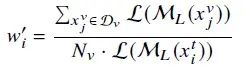
其中M𝐿是预训练的LLM,L表示sft损失,D𝑣是一个微小的有效集,𝑥𝑡𝑖是一个自生成的训练数据点。然后定义DS权重𝑤𝐷𝑆 𝑖为:
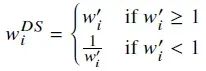
3、利用DS权重改进LLM
通过DS权重测量DSE,能够进一步过滤D𝑐中的自生成数据,排除可能具有较高DSE的数据点,所有数据点根据其DS权重𝑤𝐷𝑆 𝑖进行排序,并选择𝑘-百分位数𝜎𝑘%,使得:
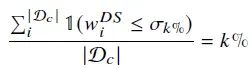
其中|·|表示集合大小,𝑤𝐷𝑆 𝑖是样本𝑥𝑖的相应DS权重
这样只有𝑤𝐷𝑆 𝑖 ≤ 𝜎𝑘%的样本被保留用于训练模型M𝐿。训练损失可以写为:
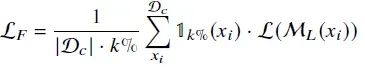
其中𝟙𝑘%(𝑥𝑖)等于𝟙(𝑤𝐷𝑆 𝑖 ≤ 𝜎𝑘%),L代表sft损失。
实验结果
1、基线
LMSI[6]:首个显著提高LLM推理能力而不需要任何外部监督的自我改进框架。LMSI的核心思想是采用多数投票来选择最可能正确的答案,从而过滤自生成数据
MoT[7]使用熵来衡量答案的不确定性,并进一步过滤数据。作者将这种技术与LMSI结合,并将其称为Entropy-filter
Self-Alignment[8]表明LLM自我评估在过滤策略中可能有帮助。作者用LMSI实现这个想法,并将其称为Self-filter
另外作者还实现了LMSI的一个变体作为参考,即RM-filter。RM-filter使用预训练的奖励模型对生成的数据进行评分,例如GENIE[9]
2、实现细节
使用Llama3-8B作为基础模型在候选答案生成阶段,让基础模型为每个问题生成15个候选答案,温度T = 1.1。每个设备的训练批次大小设置为1,梯度累积步骤为4,使用LoRA进行微调,仅在生成候选答案和评估阶段应用少样本CoT提示。
3、结果
下表显示了所有数据集的准确率结果
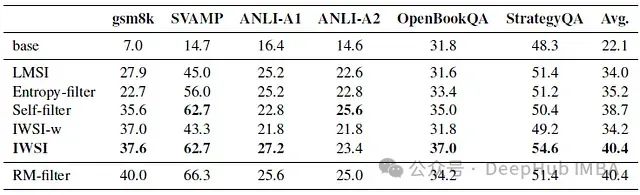
评估指标是准确率百分比,所有结果都是通过贪婪解码得出的。顶部是基础模型的性能。中间部分是自我改进基线和论文提出的方法IWSI
作为参考,在表格底部列出了RM-filter的性能,在自我改进方法(中间部分)中,IWSI是唯一一个始终优于LMSI的方法,并且在几乎所有数据集上都达到了最佳效果,这证明了过滤掉具有高DSE的自生成样本对LLM自我改进的有效性
与基础模型相比,LMSI在gsm8k上提升了310%,在SVAMP上提升了206%。IWSI进一步在gsm8k上超过LMSI 34.8%,在SVAMP上超过39.3%
4、超参数研究
下图显示了不同k值的准确率结果
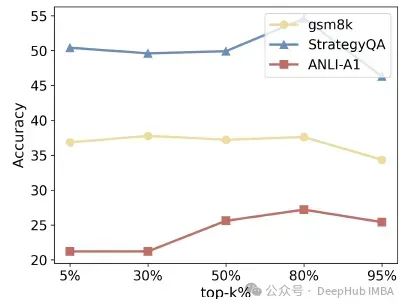
如图所示,k值过大或过小都会导致性能下降。当k很大时,会保留更多具有高DSE的样本,从而可能损害性能;如果k非常小,则保留的样本不足以支持模型训练。最佳k值范围因任务而异。一般来说,约80%是一个适当的选择。
下图显示了DS权重的不同k-百分位数σk%
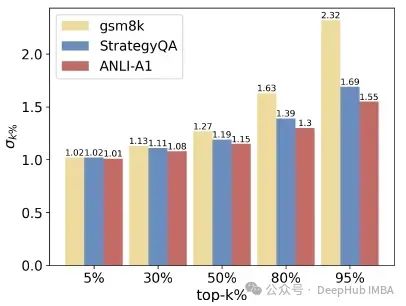
当k很小时,不同数据集的σk%相似,但随着k的增加,差异变大。这种现象表明样本DSE可被视为"高"的边界是相对的,根据不同的数据集而定。
5、有效集分析
有效集Dv在IWSI中起着至关重要的作用。它决定了DS权重的计算结果,并随后引导过滤策略。有效集组成的变化可能引入随机性,从而导致潜在的不稳定性。下图显示了IWSI前后有效集和自生成样本的分布
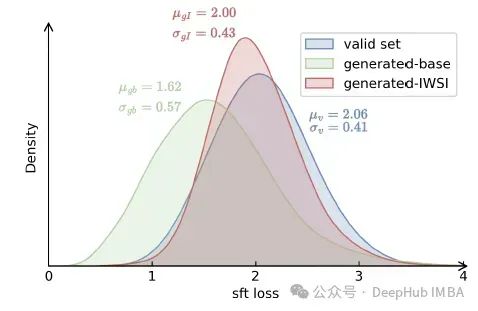
与作者的直觉相似,IWSI之前有效集样本和自生成样本之间的分布差异显著,而IWSI之后变得更加接近,说明IWSI在处理分布偏移问题上的有效性
6、正交性分析
在IWSI中,过滤策略考虑了两个因素:答案正确性(由自一致性表示)和样本DSE(由DS权重表示)。在下图中,第一行显示了答案正确性和DSE之间的关系,其中x轴是DSE间隔,y轴表示正确答案和错误答案的比例。第二行是在不同不确定性阈值u*下的DS权重概率密度函数曲线
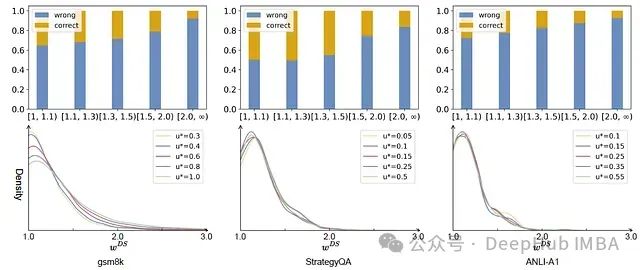
对于所有数据集,观察到随着DS权重的增加,正确答案的比例普遍呈下降趋势。正确答案的最高比例出现在[1, 1.1)区间(对于gsm8k和ANLI-A1)或[1.1, 1.3)区间(对于StrategyQA),但是正确和错误的答案在每个区间都占据了不可忽视的部分,这表明这两个因素之间存在一定程度的独立性。
7、DSE的感知
比较了同一问题的最高和最低DSE生成答案,发现具有最高DSE的案例通常明显荒谬,很容易将它们与人工编写的样本区分开来,这些样本可以分为3类:
a) 冗余样本:冗余样本在推理思路中包含无关或重复的信息,使其令人困惑。
b) 跳跃样本:跳跃样本省略了重要的推理步骤,甚至直接给出答案,使其在逻辑上不那么流畅。
c) 虚假样本:虚假样本中的推理步骤完全错误。它们只是偶然得到了正确的答案。
总结
这篇论文研究了样本DSE对LLM自我改进的影响,受重要性加权方法的启发,提出DS权重来近似DSE,并提出一个新的框架IWSI,其过滤策略全面考虑了DSE和答案正确性。实验结果表明,纳入DS权重显著提高了LLM自我改进的有效性
论文:https://arxiv.org/abs/2408.09849v1
参考文献:
- Importance Weighting Can Help Large Language Models Self-Improve by Jiang et al.arXiv:2408.09849
- Machine Learning in Non-Stationary Environments — Introduction to Covariate Shift Adaptation. by Sugiyama et al. Adaptive computation and machine learning. MIT Press
- Covariate shift adaptation by importance weighted cross validation.by Sugiyama et al. J. Mach. Learn. Res., 8:985–1005
- Direct importance estimation with model selection and its application to covariate shift adaptation. by Sugiyama et al. In NIPS, pages 1433–1440
- Rethinking importance weighting for deep learning under distribution shift. by Fang et al. In NeurIPS.
- Large language models can self-improve.by Huang et al. In EMNLP, pages 1051–1068. Association for Computational Linguistics.
- Mot: Memory-of-thoughtenables chatgpt to self-improve. by Li et al. In EMNLP, pages 6354–6374. Association for Computational Linguistics.
- Self-alignment with instruction backtranslation. by Li et al. In The Twelfth International Conference on Learning Representations
- Genie: Achieving human parity in content-grounded datasets generation. by Yehudai et al. CoRR, abs/2401.14367
作者:SACHIN KUMAR