MaskGIT: Masked Generative Image Transformer
公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)
0. 摘要
生成式 Transformer 在计算机视觉社区中经历了迅速的流行增长,用于合成高保真度和高分辨率的图像。然而,迄今为止最好的生成式 Transformer 模型仍然将图像简单地视为一系列标记,并按照光栅扫描顺序(即逐行)顺序解码图像。我们发现这种策略既不是最优的,也不是高效的。本文提出了一种新颖的图像合成范式,使用双向 Transformer 解码器,我们称之为 MaskGIT。在训练期间,MaskGIT 通过关注所有方向上的标记来学习预测随机掩蔽的标记。在推理时,模型首先同时生成图像的所有标记,然后在先前生成的基础上迭代地细化图像。我们的实验证明,MaskGIT 在ImageNet 数据集上明显优于最先进的 Transformer 模型,并且将自回归解码加速了最多 64 倍。此外,我们阐明了 MaskGIT 可以轻松扩展到各种图像编辑任务,如修复、外插和图像操作。
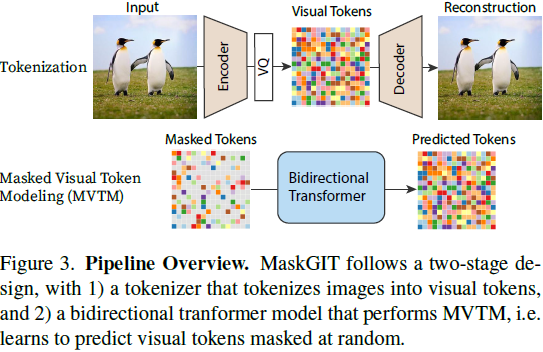
3. 方法
3.1 训练中的掩蔽视觉标记建模(Masked Visual Token Modeling,MVTM)
让 Y = [y_i]^N_(i=1) 表示通过将图像输入 VQ 编码器获得的潜在标记,其中 N 是重新整形的标记矩阵的长度,而 M = [m_i]^N_(i=1) 是相应的二进制掩码。在训练期间,我们随机抽样一部分标记,并用特殊的 [MASK] 标记替换它们。如果 m_i = 1,则将标记 y_i 替换为 [MASK],否则,当 m_i = 0时,y_i 将保持不变。
采样过程由一个掩码调度函数 γ(r) ∈ (0,1] 参数化,执行如下: 首先,我们从 0 到 1 中抽样一个比率,然后在 Y 中均匀选择 γ(r)·N (向上取整) 个标记来放置掩码,其中 N 是长度。掩码调度显著影响图像生成的质量,将在 3.3 中讨论。 用 Y_(-M) 表示对 Y 应用 mask M 后的结果。训练目标是最小化被掩蔽标记的负对数似然:

具体而言,我们将被掩蔽的 Y_(-M) 馈送到一个多层双向 transformer,以预测每个被掩蔽标记的概率

其中负对数似然被计算为基于地面真实 one-hot 标记和预测标记之间的交叉熵。注意与自回归建模的关键差异:MVTM 中的条件依赖有两个方向,允许图像生成利用通过关注图像中所有标记而获得的更丰富的上下文。
3.2 迭代解码
在自回归解码中,标记是基于先前生成的输出顺序生成的。这个过程是不可并行化的,因此对于图像来说非常慢,因为图像标记长度,例如 256 或 1024,通常比语言的长度大得多。我们引入了一种新颖的解码方法,其中图像中的所有标记都同时并行生成。可行性是因为 MTVM 的双向自注意力。
在理论上,我们的模型能够在一次传递中推断出所有标记并生成整个图像。我们发现这与训练任务的不一致性使其具有挑战性。在下面,介绍了提出的迭代解码。为了在推理时生成图像,我们从一个空白画布开始,所有标记都被掩蔽,即 Y^(0)_M。对于第 t 次迭代,我们的算法运行如下:
- 预测。给定当前迭代的被掩蔽标记 Y^(t)_M,我们的模型同时预测了所有被掩蔽位置的概率,表示为 p^(t) ∈ R^(N x K)。
- 采样。在每个被掩码位置 i,我们基于其在代码本中所有可能标记的预测概率 p^(t)_i ∈ R^K 进行标记抽样。在抽样到标记 y^(t)_i 后,其相应的预测分数被用作 “置信度” 分数,表示模型对该预测的信任程度。对于 Y^(t)_M 中的未被掩蔽的位置,我们简单地将其置信度分数设置为1.0。
- 掩蔽调度。我们根据掩码调度函数通过 n = γ(r)·N (向上取整) 计算要掩蔽的标记数量,其中 N 是输入长度,T 是总迭代次数。
- 掩蔽。我们通过在 Y^(t)_M 中掩蔽 n 个标记来获得 Y^(t+1)_M。 迭代 t+1 的掩码 M^(t+1) 是从以下计算的,其中 c_i 是第 i 个标记的置信度分数。


解码算法在 T 步中合成一幅图像。 在每次迭代中,模型同时预测所有标记,但仅保留最有信心的标记。其余的标记被掩蔽并在下一次迭代中重新预测。 掩蔽比例逐步减小,直到在 T 次迭代内生成所有标记。在实践中,掩蔽标记是通过温度退火(temperature annealing)随机抽样以鼓励更多的多样性,并且我们将在 4.4 中讨论其效果。图 2 说明了我们解码过程的示例。它在 T = 8 次迭代中生成一幅图像,每次迭代的未掩蔽标记在网格中突出显示,例如,当 t - 1 时,我们仅保留 1 个标记并掩蔽其余的标记。
3.3 掩蔽设计
我们发现掩蔽设计显著影响图像生成的质量。我们通过掩蔽调度函数 γ(·) 对掩蔽过程进行建模,该函数计算给定潜在标记的掩蔽比例。如前所述,该函数在训练和推理中均被使用。在推理时,以解码进展 0/T, 1/T, ..., (T-1)/T 作为掩蔽比例。在训练中,我们在 [0, 1) 中随机采样一个比率 r 以模拟各种解码场景。
BERT 使用固定的掩蔽比例为 15% [11],即始终掩蔽 15% 的标记,这对于我们的任务是不适当的,因为我们的解码器需要从头生成图像。因此,需要新的掩蔽调度。在讨论具体方案之前,我们首先考察了掩蔽调度函数的性质。首先,对于 r ∈ [0, 1], γ(·) 需要是一个在 0 到 1 范围内的连续函数。其次,γ(·) 应该相对于 r (单调) 递减,并且满足 γ(·) → 1 和 γ(·) → 0。第二个属性确保了我们解码算法的收敛性。


这篇论文考虑了常见的函数并进行简单的转换,使其满足特定属性。图 8 可视化了这些函数,它们被分为三组:(注:国外凹凸的定义与国内相反)
- 线性函数是一个直接的解决方案,每次掩蔽相同数量的标记。
- 凹函数捕捉到图像生成遵循从少到多信息流的直觉。一开始,大多数标记都被掩蔽,因此模型只需要对其感到自信的少数正确预测。到最后,掩蔽比例急剧下降,迫使模型做出更多的正确预测。在这个过程中,有效信息在增加。凹函数家族包括余弦(cosine)、平方(square)、立方(cubic)和指数函数(exponential)。
- 凸函数相反,实现了一个从多到少的过程。模型需要在最初的几次迭代中完成绝大多数标记。该家族包括平方根(square root)和对数函数(logarithmic)。
我们在 4.4 中以实证方法比较了上述的掩蔽调度函数,发现余弦函数在我们所有的实验中表现最佳。
4. 实验
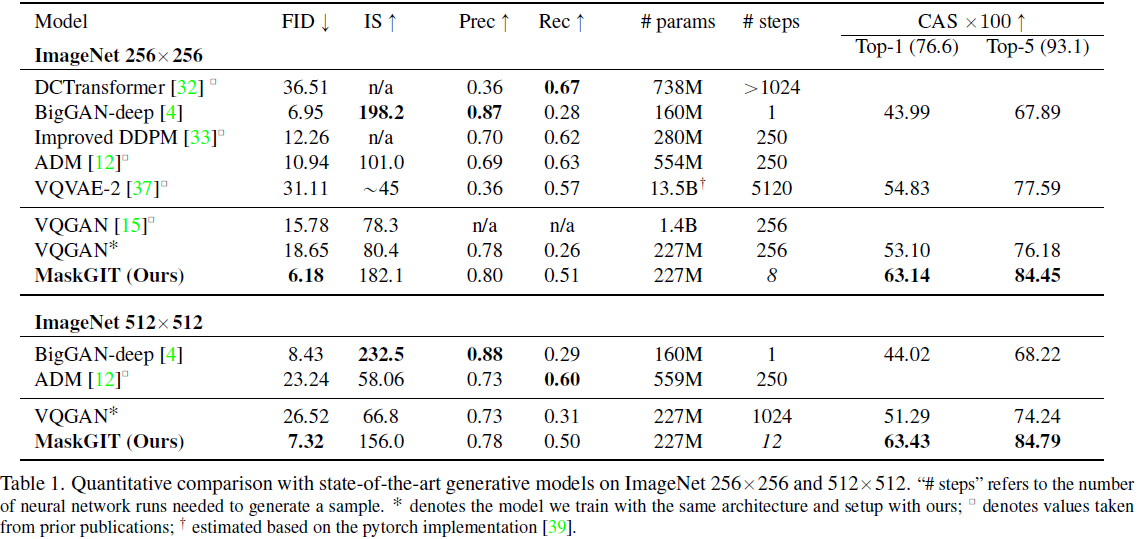



版权归原作者 EDPJ 所有, 如有侵权,请联系我们删除。