R实战 | 限制性立方样条(RCS)

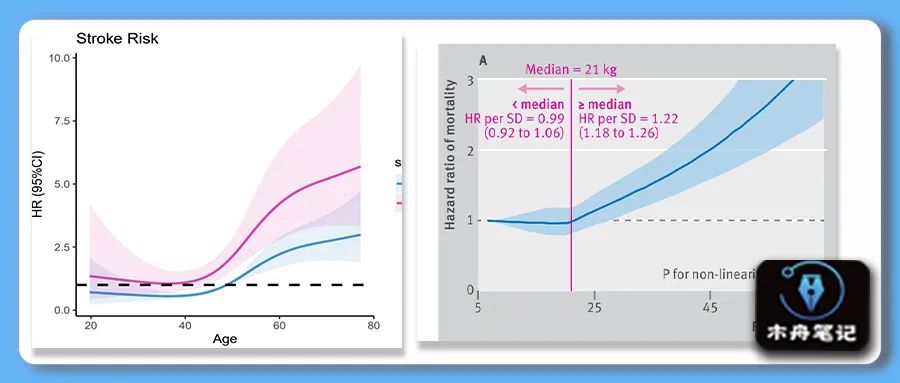
RCS

在科学研究中，我们经常构建回归模型来分析

自变量

和

因变量

之间的关系。大多数的回归模型有一个重要的假设就是自变量和因变量呈

线性关联

。当自变量和因变量之间为非线性关系时，可以将

连续型变量

转化为

分类变量

，但是分类变量的

类别数目

以及

节点位置

的选择一般会带有主观性并且分类变量会损失部分信息；也可以直接拟合自变量和因变量之间的非线性关系，但是直接构建多项式回归可能存在过度拟合、共线性等问题。因此，一个更好的解决方法是拟合自变量与因变量之间的非线性关系，「限制性立方样条」(Restricted cubic spline，RCS)就是分析非线性关系的最常见的方法之一。

样条

（spline）原本是指是一种灵活的细木条或金属条，用来绘制平滑曲线。样条曲线本质是一个

分段多项式函数

，此函数受限于某些控制点，称为 “节点”，节点放置在数据范围内的多个位置，多项式的类型以及节点的数量和位置决定了样条曲线的类型。

立方

则指的是函数为3次多项式。

限制

是在回归样条的基础上附加要求：样条函数在自变量数据范围两端的两个区间

[X1,X2)

和

(Xn-1,Xn]

内是线性函数。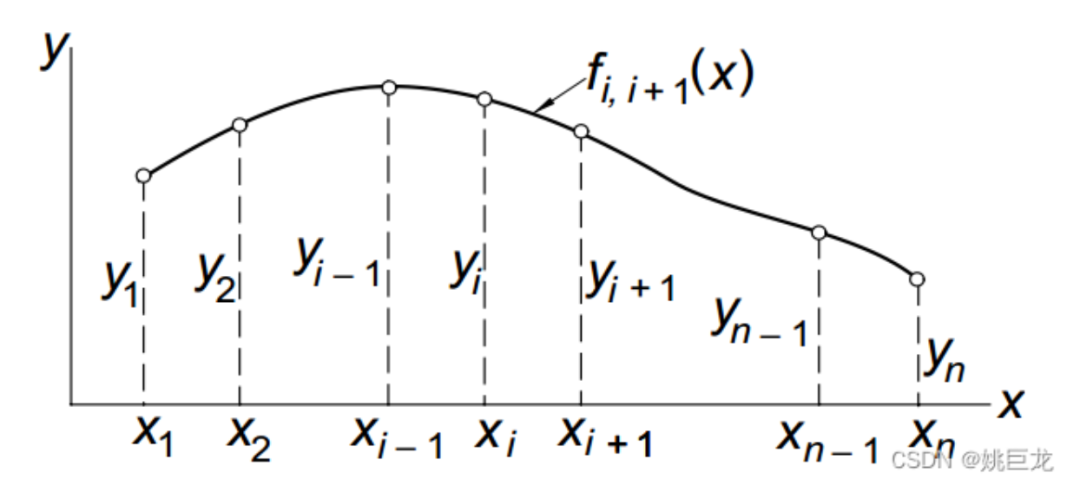

RCS曲线

RCS

节点

的数量比位置更重要。由于节点个数的选择和自由度有关, 所以当样本量比较大的时候可以取较多的节点。但是节点越多, 自由度越大, 模型越复杂, 越难解在「«Regression Modeling Strategies»」这本书中，Harrell 建议节点数为4时，模型的拟合效果较好，即同时可以兼顾曲线的平滑程度以及避免过拟合造成的精确度降低。当样本量较大时，5个节点是更好的选择。小样本（n<30）可以选择3个节点。当节点的个数为2时，得到的拟合曲线就是一条直线。大多数研究者推荐的节点为3-5个。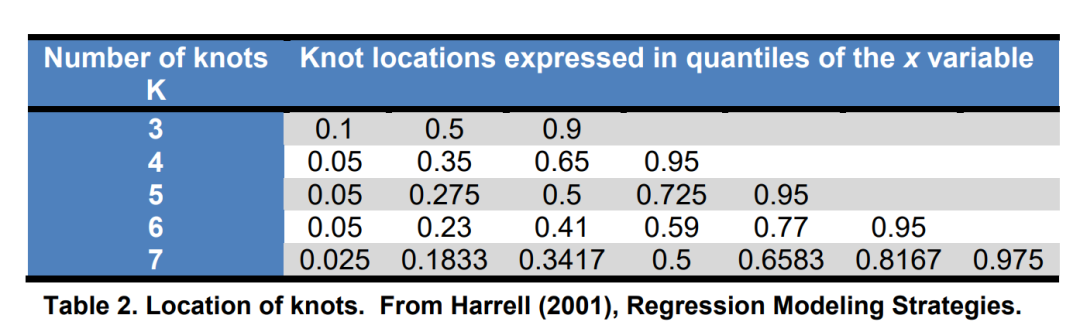

一个例子

❝

Lee DH, Keum N, Hu FB, et al. Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study. BMJ. 2018;362:k2575. Published 2018 Jul 3. doi:10.1136/bmj.k2575

❞

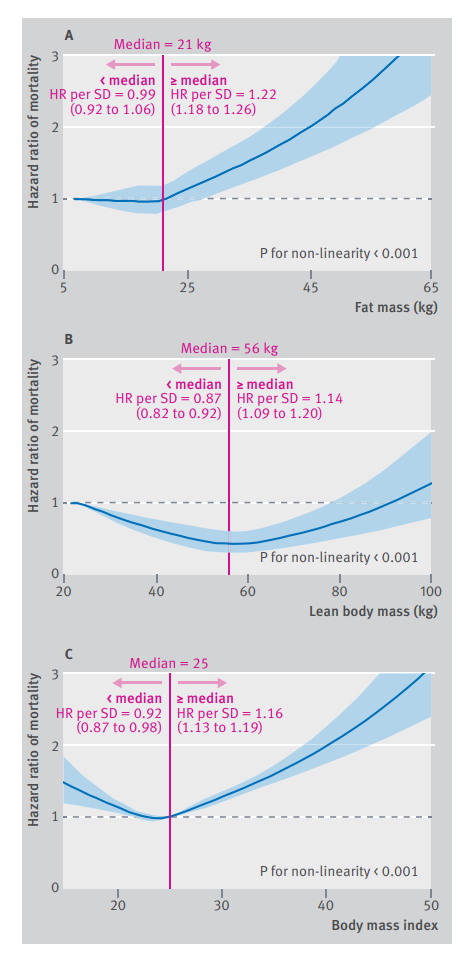
Association of predicted body composition and body mass index (BMI)* with all cause mortality in men

❝

如图，为了探究预测的FM、LBM和BMI与男性全因死亡率的关系，作者分别对这三个因素做了RCS分析。

❞

RCS实战

#加载所需要的包
library(ggplot2)
#install.packages('rms')
library(rms)   
# 导入示例数据
data <- read.csv('test.csv')
head(data)

> head(data)
       age    sex      time death
1 60.57519   Male  3.094579     1
2 42.11447   Male  1.574237     0
3 54.86611   Male  3.239313     0
4 55.82207   Male 12.495977     0
5 52.48256 Female  3.252534     0
6 46.12436   Male  2.836695     0

# 对数据进行打包，整理
dd <- datadist(data) #为后续程序设定数据环境
options(datadist='dd') #为后续程序设定数据环境
# 拟合模型
fit<- cph(Surv(time,death) ~ rcs(age,4) + sex,data=data)  # 节点数设为4
# 非线性检验
# P<0.05为存在非线性关系
anova(fit)

> anova(fit)
                Wald Statistics          Response: Surv(time, death) 

 Factor     Chi-Square d.f. P     
 age        57.75      3    <.0001
  Nonlinear  8.17      2    0.0168
 sex        18.75      1    <.0001
 TOTAL      75.63      4    <.0001

# 查看HR预测表
# 看一下预测的HR所对因的age
HR<-Predict(fit, age,fun=exp,ref.zero = TRUE)
head(HR)

> head(HR)
       age  sex      yhat     lower    upper
1 19.71985 Male 0.7087866 0.2403429 2.090257
2 20.00869 Male 0.7052492 0.2429359 2.047356
3 20.29754 Male 0.7017294 0.2455536 2.005363
4 20.58638 Male 0.6982271 0.2481960 1.964258
5 20.87523 Male 0.6947423 0.2508632 1.924024
6 21.16408 Male 0.6912750 0.2535552 1.884643

Response variable (y):  

Adjust to: sex=Male  

Limits are 0.95 confidence limits

# 绘图
ggplot()+
  geom_line(data=HR, aes(age,yhat),
            linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+
  geom_ribbon(data=HR, 
              aes(age,ymin = lower, ymax = upper),
              alpha = 0.1,fill="#0070b9")+
  theme_classic()+
  geom_hline(yintercept=1, linetype=2,size=1)+
  geom_vline(xintercept=48.89330,size=1,color = '#d40e8c')+ #查表HR=1对应的age
  labs(title = "Stroke Risk", x="Age", y="HR (95%CI)")

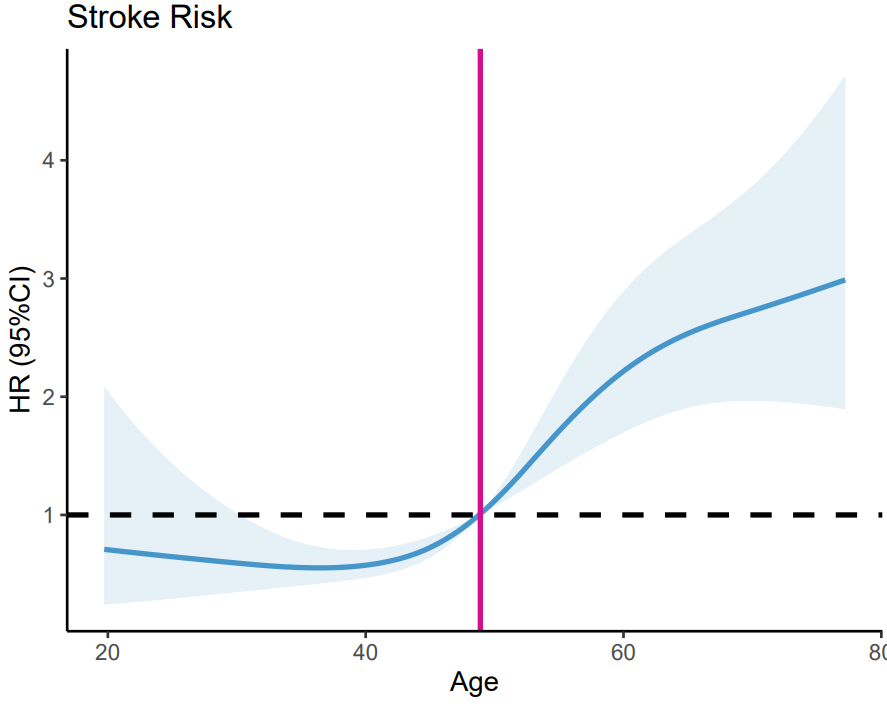
RCS1

❝

可以看到，年龄<49岁，死亡风险随年龄变化不是很明显；年龄>49岁后，死亡风险随年龄的增加而增加。

❞

分组

### 性别分组
HR1 <- Predict(fit, age, sex=c('Male','Female'),
               fun=exp,type="predictions",
               ref.zero=TRUE,conf.int = 0.95,digits=2)
HR1
ggplot()+
  geom_line(data=HR1, aes(age,yhat, color = sex),
            linetype="solid",size=1,alpha = 0.7)+
  geom_ribbon(data=HR1, 
              aes(age,ymin = lower, ymax = upper,fill = sex),
              alpha = 0.1)+
  scale_color_manual(values = c('#0070b9','#d40e8c'))+
  scale_fill_manual(values = c('#0070b9','#d40e8c'))+
  theme_classic()+
  geom_hline(yintercept=1, linetype=2,size=1)+
  labs(title = "Stroke Risk", x="Age", y="HR (95%CI)")

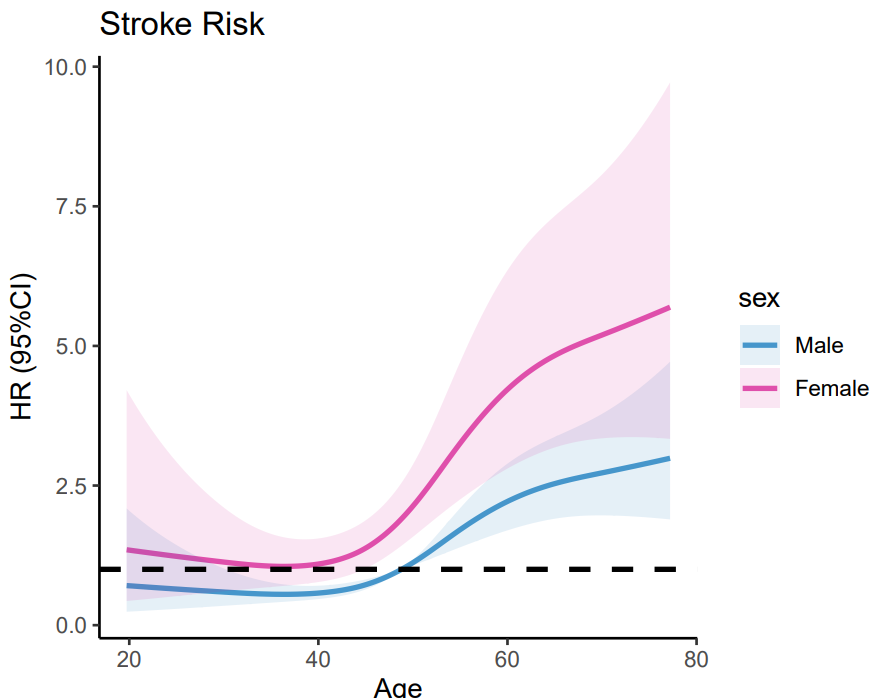
RCS2

示例数据和代码领取

点赞

、

在看

本文，分享至朋友圈

集赞25个

并

保留30分钟

，截图发至微信

mzbj0002

领取。

「木舟笔记2022年度VIP可免费领取」。

木舟笔记2022年度VIP企划

「权益：」

「2022」年度木舟笔记所有推文示例数据及代码(「在VIP群里实时更新」)。资源合集
木舟笔记「科研交流群」。
「半价」购买跟着Cell学作图系列合集(免费教程+代码领取)|跟着Cell学作图系列合集。

「收费：」

「99￥/人」。可添加微信：

mzbj0002

转账，或直接在文末打赏。

参考

https://blog.csdn.net/weixin_43645790/article/details/125285467
限制性立方样条图，一种美的不行的趋势性分析方法（附R语言详细教程
Restricted cubic splines. A spline is a drafting tool for drawing… | by Peter Flom | Towards Data Science
R语言绘制限制性立方样条（Restricted cubic spline，RCS） - 简书 (jianshu.com)

往期内容

CNS图表复现|生信分析|R绘图资源分享&讨论群！
组学生信| Front Immunol |基于血清蛋白质组早期诊断标志筛选的简单套路
(免费教程+代码领取)|跟着Cell学作图系列合集
Q&A | 如何在论文中画出漂亮的插图？
跟着 Cell 学作图 | 桑葚图(ggalluvial)
R实战 | Lasso回归模型建立及变量筛选
跟着 NC 学作图 | 互作网络图进阶(蛋白+富集通路)(Cytoscape)
R实战 | 给聚类加个圈圈(ggunchull)
R实战 | NGS数据时间序列分析(maSigPro)
跟着 Cell 学作图 | 韦恩图(ggVennDiagram)

木舟笔记矩阵

标签：机器学习 python 人工智能

本文转载自: https://blog.csdn.net/weixin_45822007/article/details/126357743
版权归原作者 木舟笔记 所有，如有侵权，请联系我们删除。

R实战 | 限制性立方样条(RCS)

一个例子

RCS实战

分组

示例数据和代码领取

木舟笔记2022年度VIP企划

参考

往期内容

发表评论

“R实战 | 限制性立方样条(RCS)”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航