堆排序
堆排序是利用树的结构进行的，常常用于选出最大/最小的N个数，效率很高
树可以用链表表示，也可以用数组表示，这里我们先用数组来实现堆排序
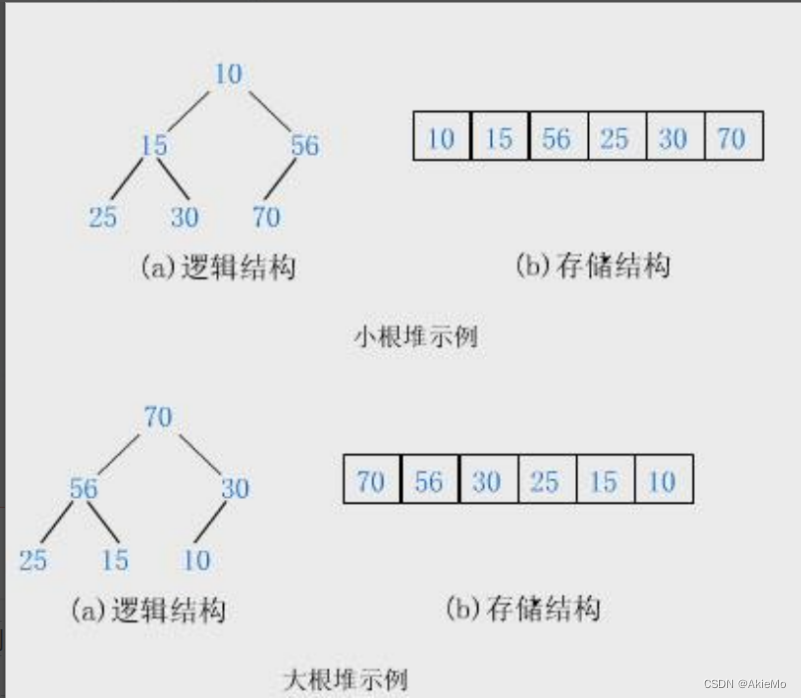
** 首先我们要先把一个数组构造成一个堆，只有成为了一个堆之后才能进行向上/向下调整**
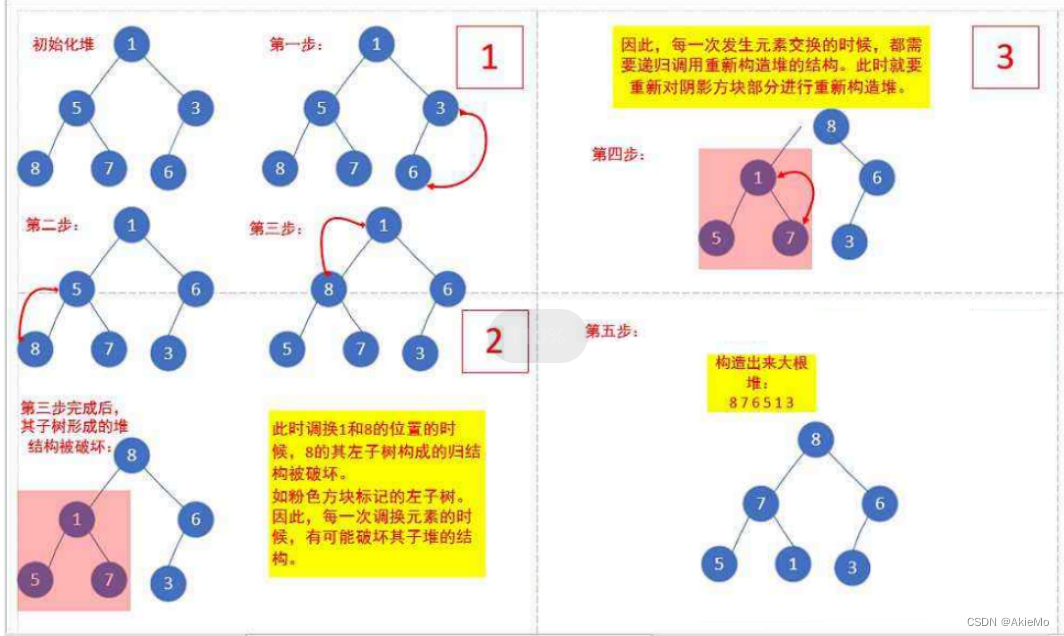
将问题一个一个细分，因为一个乱的数如果直接从根开始进行向上/向下进行排序的话肯定是不行的，所以我们可以从最后一个非叶子节点开始往前进行向上调整，而这里为什么要从最后一个非叶子节点开始呢？因为单个叶子节点不需要调整，也无法进行调整，如图，第一个非叶子节点就是3，从而对3和6进行调整，一直到1位置为止，这时候就已经把数组排成了一个堆了。
而如何进行向上/向下调整呢？
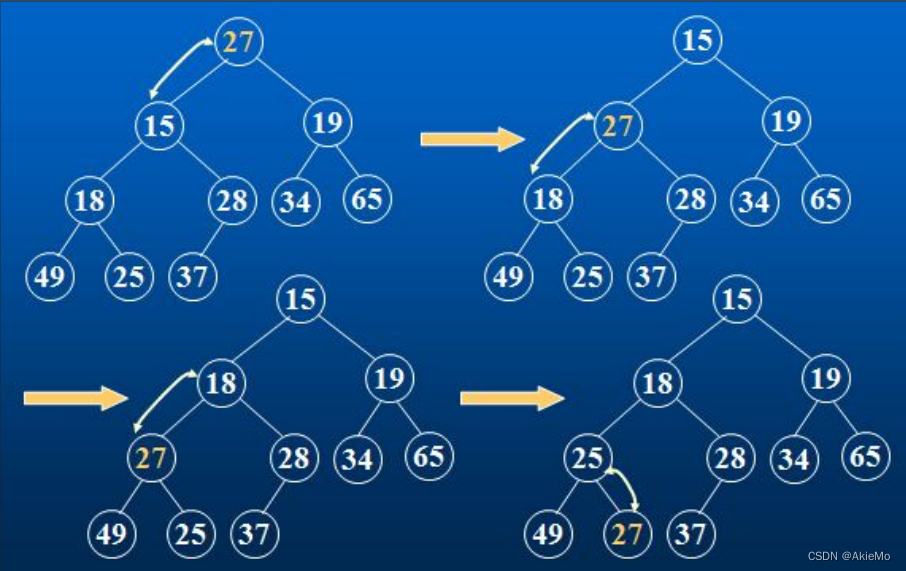对于向下调整而言，调成一个小堆我，就是父亲节点一定小于孩子节点。
而第一个问题就是如何找到左右孩子中较小的那一个呢？为了代码的简洁，可以直接找到左孩子，而右孩子就是左孩子+1，child=parent2+1，*以下为代码实现:
//向下调整(小堆)
void AdjustDown(int *a, int n, int parent) {
int child = parent * 2 + 1;//左孩子，右孩子为左孩子+1
while (child < n) {
//child+1不能大于n，然后再选出左右孩子中小的那一个
if (child + 1 < n && a[child + 1] < a[child]) {
child++;//拿到右孩子
}
if (a[child] < a[parent]) {
//如果孩子节点小于父亲节点，则进行交换
Swap(&a[child], &a[parent]);
//父亲和孩子继续交换，继续向下调整
parent = child;
child = parent * 2 + 1;
} else {
break;
}
}
}
交换函数Swap:
void Swap(int *child, int *parent) {
int tmp = *child;
*child = *parent;
*parent = tmp;
}
现在就可以将数组构造成堆了，代码实现:
void CreateHeap(int *a, int n) {
//找到最后一个非叶子节点的节点
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(a, n, i);
}
}
总代码:
#include <stdio.h>
void Swap(int *child, int *parent) {
int tmp = *child;
*child = *parent;
*parent = tmp;
}
//堆排序
//向下调整(小堆)
void AdjustDown(int *a, int n, int parent) {
int child = parent * 2 + 1;//左孩子，右孩子为左孩子+1
while (child < n) {
//child+1不能大于n，然后再选出左右孩子中小的那一个
if (child + 1 < n && a[child + 1] < a[child]) {
child++;//拿到右孩子
}
if (a[child] < a[parent]) {
//如果孩子节点小于父亲节点，则进行交换
Swap(&a[child], &a[parent]);
//父亲和孩子继续交换，继续向下调整
parent = child;
child = parent * 2 + 1;
} else {
break;
}
}
}
//建堆
void CreateHeap(int *a, int n) {
//找到最后一个非叶子节点的节点
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(a, n, i);
}
}
int main(void) {
int arr[] = { 3, 8, 9, 18, 7, 5, 10, 87, 21, 99, 76, 100 };
CreateHeap(arr, 12);
for (int i = 0; i < 12; i++) {
printf("%d ", arr[i]);
}
return 0;
}
运行结果
画出树的结构为:
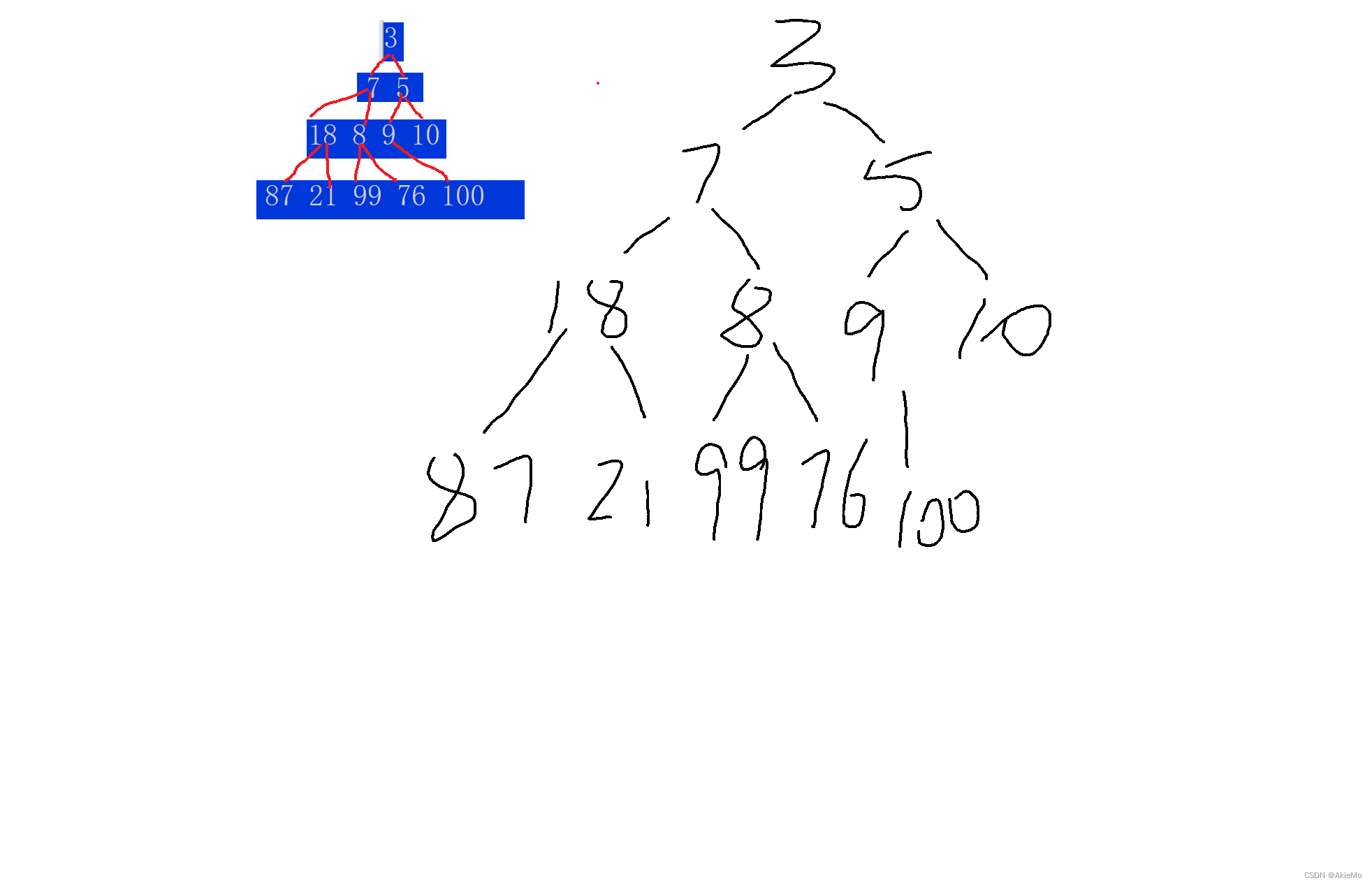
可以看出，这个数组已经变成一个小堆了。
接下来就可以进行堆排序了，那么如何进行堆排序呢？
如果要排升序，就建立一个大堆，选出来最大的数，然后最后一个数和第一个数交换，再把最后一个数不看作堆里的数1，进行向下调整即可
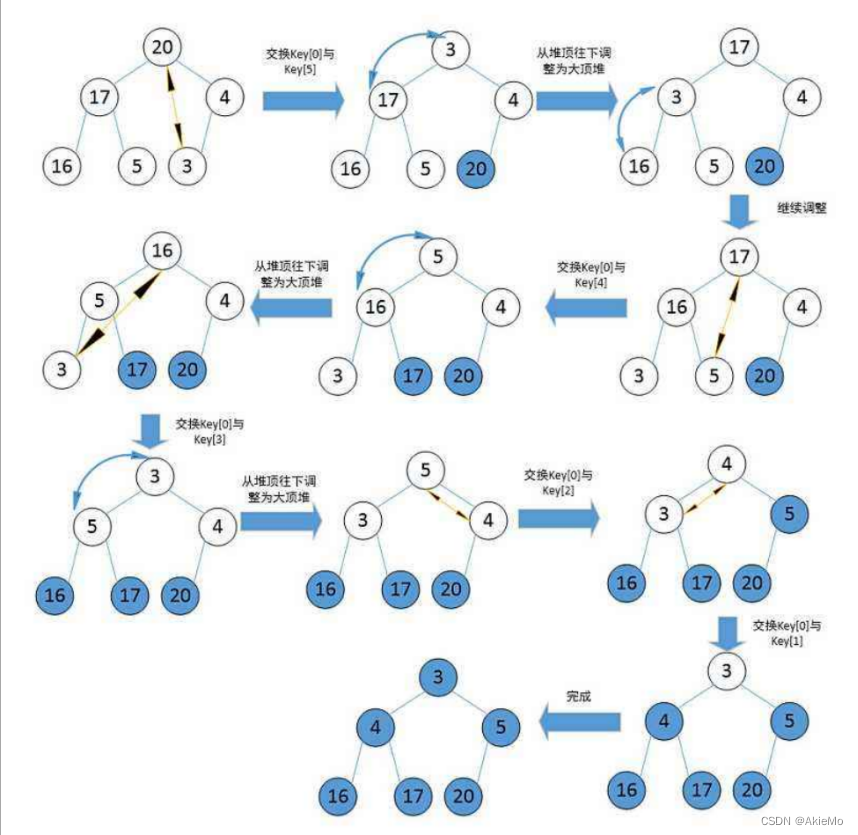
代码实现:
void HeapSort(int *a, int n) {
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(a, n, i);
}
int end = n - 1;
while (end >= 0) {
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
运行结果:
这样就排序成功了。
总代码:
#include <stdio.h>
void Swap(int *child, int *parent) {
int tmp = *child;
*child = *parent;
*parent = tmp;
}
//堆排序
//向下调整(小堆)
void AdjustDown(int *a, int n, int parent) {
int child = parent * 2 + 1;//左孩子，右孩子为左孩子+1
while (child < n) {
//child+1不能大于n，然后再选出左右孩子中小的那一个
if (child + 1 < n && a[child + 1] > a[child]) {
child++;//拿到右孩子
}
if (a[child] > a[parent]) {
//如果孩子节点小于父亲节点，则进行交换
Swap(&a[child], &a[parent]);
//父亲和孩子继续交换，继续向下调整
parent = child;
child = parent * 2 + 1;
} else {
break;
}
}
}
//建堆
void CreateHeap(int *a, int n) {
//找到最后一个非叶子节点的节点
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(a, n, i);
}
}
//堆排序(大堆的条件下),进行升序
void HeapSort(int *a, int n) {
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(a, n, i);
}
int end = n - 1;
while (end >= 0) {
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
int main(void) {
int arr[] = { 3, 8, 9, 18, 7, 5, 10, 87, 21, 99, 76, 100 };
HeapSort(arr, 12);
for (int i = 0; i < 12; i++) {
printf("%d ", arr[i]);
}
return 0;
}
选择排序
选择排序，顾名思义就是选择某个数进行排序，这里我们可以遍历一次数据，找到最小值和最大值，将最小值放在第一个位置，最大值放在最后一个位置，然后再将区间缩小，一次类推，但这里会有一个bug，那就是当第一个数就是最大值的时候是无法正确进行排序的。
这时候就需要进行修正
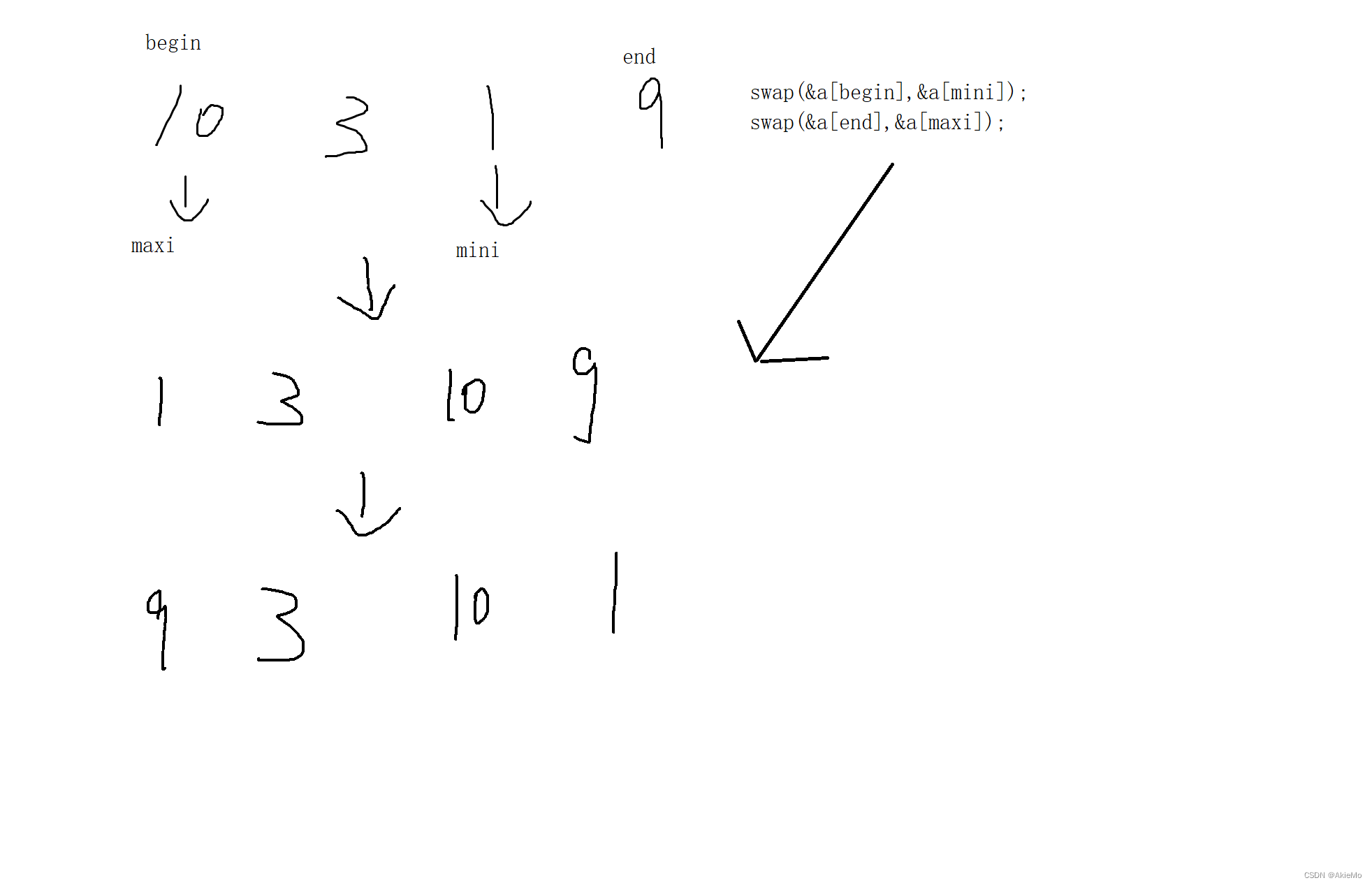
解决方法就是加一个判断，如果begin==maxi，那么maxi=mini
代码实现
#include <stdio.h>
void Swap(int* child, int* parent) {
int tmp = *child;
*child = *parent;
*parent = tmp;
}
void SelectSort(int* a, int n) {
int begin = 0, end = n - 1;
while (end > begin) {
int mini = begin, maxi = begin;
for (int i = begin; i <= end; i++) {
if (a[i] < a[mini]) {
mini = i;
}
if (a[i] > a[maxi]) {
maxi = i;
}
}
Swap(&a[begin], &a[mini]);
if (begin == maxi) {
maxi = mini;
}
Swap(&a[end], &a[maxi]);
end--;
begin++;
}
}
int main(void) {
int arr[] = { 100, 8, 6, 89, 26, 83, 52, 12, 90, 0 };
SelectSort(&arr, 10);
for (int i = 0; i < 10; i++) {
printf("%d ", arr[i]);
}
return 0;
}
直接插入排序
直接插入排序是一种简单的插入排序法，其基本思想是：把待排序的记录按其关键码值的大小逐个插入到一
个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。
实际中我们玩扑克牌时，就用了插入排序的思想
从要插入的位置开始，设这个位置为end,用该位置的数值从后往前比较，如果能找到比它小的数，则a[end+1]=x;
代码实现:
#include <stdio.h>
void InsertSort(int *a, int n) {
for (int i = 0; i < n - 1; i++) {
int end = i;
int x = a[end + 1];
while (end >= 0) {
if (a[end] > x) {
a[end + 1] = a[end];
end--;
} else {
break;
}
}
a[end + 1] = x;
}
}
int main(void) {
int arr[] = {100, 520, 123, 98, 56, 23, 87, 12, 66, 99};
InsertSort(arr, 10);
for (int i = 0; i < 10; i++) {
printf("%d ", arr[i]);
}
return 0;
}
运行结果:
希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个
组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工
作。当到达=1时，所有记录在统一组内排好序。
希尔排序其实就是在直接插入排序的基础上进行了改良，直接插入排序的快慢取决于数组是否接近有序，是的话则很快，反之较慢，而希尔排序就是先将数组接近有序，再进行直接插入排序
如图所示，当gap等于2的时候，4 2 5 8 5为一组，1 3 9 6 7为一组，对这两组数据进行排序，可以使得数组的数据接近有序，当gap越大，越接近无序，反之则接近有序，当gap=1的时候，就是直接插入排序了，又因为gap也是数据的组数，所以可以操作gap来进行排序
代码实现：
#include <stdio.h>
void ShellSort(int *a, int n) {
int gap = n;
while (gap > 1) {
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++) {
int end = i;
int x = a[end + gap];
while (end >= 0) {
if (a[end] > x) {
a[end + gap] = a[end];
end -= gap;
} else {
break;
}
}
a[end + gap] = x;
}
}
}
int main(void) {
int arr[] = {100, 520, 0, 78, 66, 99, 123, 97, 12, 2};
ShellSort(arr, 10);
for (int i = 0; i < 10; i++) {
printf("%d ", arr[i]);
}
return 0;
}
版权归原作者 AkieMo 所有， 如有侵权，请联系我们删除。