
在这篇文章中,我们将学习10个最重要的模型性能度量,这些度量可用于评估分类模型的模型性能。
以下是我们将通过示例以相互关联的方式研究的10个指标:
- Confusion Matrix
- Type I Error
- Type II Error
- Accuracy
- Recall or True Positive Rate or Sensitivity
- Precision
- Specificity
- F1 Score
- ROC Curve- AUC Score
- PR Curve
一旦我们了解了适当的用法以及如何根据问题陈述来解释这些度量,那么衡量分类模型的强度就不是问题了。
我们将使用一个数据集的例子,它有yes和no标签,用于训练逻辑回归模型。这个用例可以是任何分类问题-垃圾邮件检测、癌症预测、损耗率预测、活动目标预测等。我们将在本文需要时参考特殊用例。目前,我们将考虑一个简单的逻辑模型,它必须预测是或否。
首先,逻辑模型可以给出两种输出:
1.它以输出值的形式给出类标签(是/否、1/0、恶性/良性、吸引/保留、垃圾邮件/非垃圾邮件等)
2.它给出了介于0到1之间的概率值作为输出值,以表示某个特定观察事件的可能性或可能性。
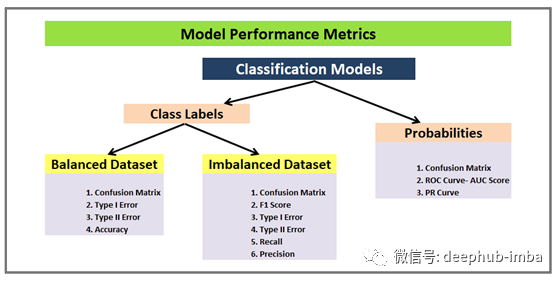
类标签场景可以进一步细分为平衡或不平衡数据集,这两种情况都不能/不应该基于类似的度量进行判断。有些指标更适合但不是另一个,反之亦然。类似地,概率场景有不同于类标签的模型性能度量。
下面是流程图,这是一个完美的总结,也是这篇文章的一个完美的前言,我们将在最后再次回顾这个流程图,以确保我们了解所有的指标。
Confusion Matrix

我们从一个开发数据集开始,同时构建任何统计或ML模型。把数据集分成两部分:训练和测试。保留测试数据集,并使用训练数据集训练模型。一旦模型准备好预测,我们就尝试在测试数据集上进行预测。一旦我们将结果分割成一个类似于上图所示的矩阵,我们就可以看到我们的模型有多少能够正确预测,有多少预测是错误的。
我们用测试数据集中的数字填充以下4个单元格(例如,有1000个观察值)。

TP(真阳性):该列的实际标签在测试数据集中为“是”,我们的logistic回归模型也预测为“是”。(500次观察)
TN(真阴性):在测试数据集中,该列的实际标签为“否”,而我们的logistic回归模型也预测为“否”。(200次观察)
FP(假阳性):该列的实际标签在测试数据集中为“否”,但我们的logistic回归模型预测为“是”。(100次观察)
FN(假阴性):在测试数据集中,该列的实际标签为“是”,但我们的逻辑回归模型预测为“否”。(200次观察)
这4个单元构成了“混淆矩阵”,就像在矩阵中一样,它可以通过清晰地描绘模型的预测能力来缓解对模型优度的所有混淆。
混淆矩阵是一个表,通常用于描述一个分类模型(或“分类器”)在一组已知真实值的测试数据上的性能
Type I Error

第1类错误也称为假阳性,当分类模型错误地预测最初错误观察的真实结果时发生。
例如:假设我们的逻辑模型正在处理一个垃圾邮件而不是垃圾邮件的用例。如果我们的模型将一封其他重要的电子邮件标记为垃圾邮件,那么这是我们的模型的类型I错误的一个例子。在这个特别的问题陈述中,我们对尽可能减少类型I错误非常敏感,因为进入垃圾邮件的重要电子邮件可能会产生严重的影响。
Type II Error

第2类错误也被称为假阴性,当分类模型错误地预测了最初真实观察结果的假结果时就会发生。
例如:假设我们的逻辑模型正在处理一个用例,它必须预测一个人是否患有癌症。如果我们的模型将患有癌症的人标记为健康人并对其进行了错误分类,那么这就是我们的模型的第二类错误的一个例子。在这个特别的问题陈述中,我们对尽可能减少II型错误非常敏感,因为如果疾病继续在患者中未被诊断,这种情况下的假阴性可能导致死亡。
Accuracy
现在,上面讨论的三个度量是通用度量,与有的培训和测试数据类型以及为问题陈述部署的分类算法类型无关。
我们现在正在讨论非常适合特定类型数据的度量。
让我们从这里开始讨论准确性,这是一个最适合用于平衡数据集的度量。
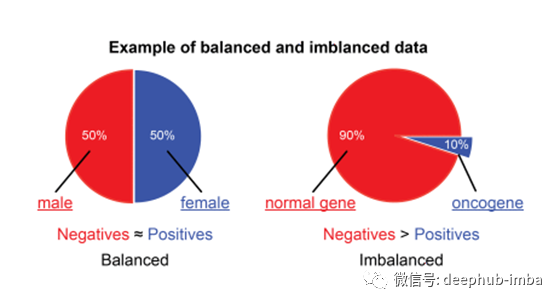
一个平衡的数据集是1和0,是和否,正和负都由训练数据平均表示的数据集。另一方面,如果两个类标签的比率有偏差,那么我们的模型将偏向一个类别。
假设我们有一个平衡的数据集,让我们学习什么是准确性。
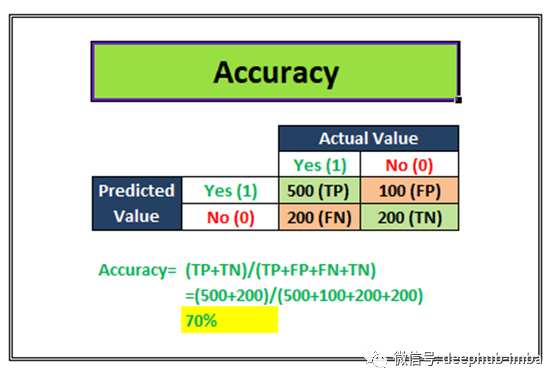
准确度是指测量结果接近真实值。它告诉我们,我们的分类模型能够多准确地预测问题陈述中给出的类标签。
例如:假设我们的分类模型试图预测客户流失情况。在上图中,在实际吸引的700个客户中(TP+FN),该模型能够正确地对500个吸引的客户进行分类(TP)。同样,在总共300个保留客户(FP+TN)中,该模型能够正确地对200个保留客户(TN)进行分类。
Accuracy= (TP+TN)/Total customers
在上面的场景中,我们看到模型在1000个客户的测试数据集上的准确率是70%。
现在,我们了解到准确性是一个度量标准,应该只用于平衡的数据集。为什么会这样?让我们看一个例子来理解这一点。

在这个例子中,这个模型是在一个不平衡的数据集上训练的,甚至测试数据集也是不平衡的。准确度指标的得分为72%,这可能给我们的印象是,我们的模型在分类方面做得很好。但是,仔细看,这个模型在预测负面的类标签方面做得很糟糕。在100个总的阴性标记观察中,它只预测了20个正确的结果。这就是为什么如果您有一个不平衡的数据集,就不应该使用精度度量。
下一个问题是,如果您有一个不平衡的数据集,将使用什么?答案是Recall和Precision。让我们进一步了解这些。
Recall/ Sensitivity/ TPR
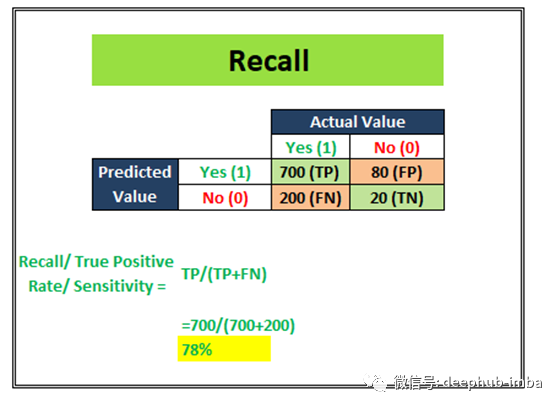
Recall/ Sensitivity/ TPR(真阳性率)试图回答以下问题:
哪些实际阳性被正确识别?

上面的图像告诉我们召回分数是78%。召回通常用于真相检测最为重要的用例中。例如:癌症预测、股市分类等。在这里,问题陈述要求最小化假阴性,这意味着最大化召回/敏感度。
Precision
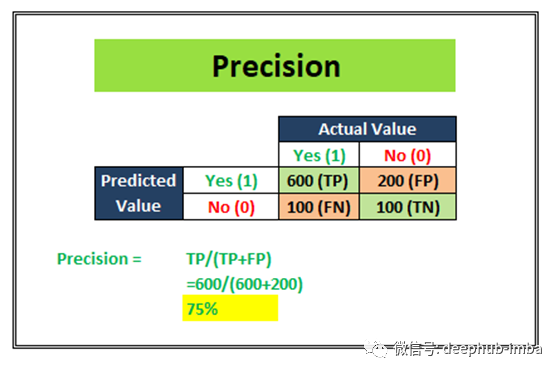
精确性尝试回答以下问题:
什么比例的阳性鉴定是正确的?

上图所示的示例表明,精度得分为75%。精度通常用于最重要的情况,即不存在大量误报。例如:在垃圾邮件检测案例中,正如我们前面所讨论的,假阳性将是一个观察结果,它不是垃圾邮件,但根据我们的分类模型被归类为垃圾邮件。过多的误报可能会破坏垃圾邮件分类模型的目的。因此,在这种情况下,判断模型性能的精确性非常方便。
Specificity

特异性(也被称为真阴性率)测量实际阴性的比例被正确地识别为这样。
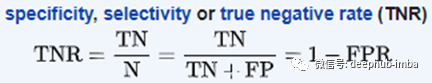
垃圾邮件检测分类器的例子,我们了解精度。继续使用那个例子,特异性告诉我们我们的模型能够准确分类多少个阴性。在这个例子中,我们看到专一性=33%,这对于垃圾邮件检测模型来说不是一个好的分数,因为这意味着大多数非垃圾邮件被错误地归类为垃圾邮件。我们可以通过观察特异性度量得出结论,这个模型需要改进。
F1 Score
我们分别讨论了第6点和第7点中的回忆和精确性。我们知道,有些问题陈述中,较高的查全率优先于较高的查准率,反之亦然。
但是有一些用例,其中的区别不是很清楚,作为开发人员,我们希望同时重视召回和精确性。在这种情况下,还可以使用另一个度量标准-F1分数。它依赖于精确性和召回率。
在二元分类的统计分析中,F1分数(也可以是F分数或F测度)是测试准确性的度量。它同时考虑了测试的精确性p和召回率r来计算分数

在讨论最后两个指标之前,下面是Wikipedia上提供的一个很好的摘要表,它涵盖了我们在本文中讨论过的所有指标。放大看看图像是否不清晰。

现在,我们已经到了最后一站了。到目前为止,我们已经讨论了预测类标签的分类模型的模型性能度量。现在,让我们研究基于概率的模型的度量。
ROC Curve- AUC Score
曲线下面积(AUC)、受试者工作特性曲线(ROC)
这是衡量模型性能的最重要指标之一,在数据科学家中广受欢迎。
让我们从一个例子开始理解这一点。我们有一个分类模型,它给出了0-1之间的概率值来预测一个人是否肥胖的概率。接近0的概率分数表示考虑中的人肥胖的概率非常低,而接近1的概率值表示人肥胖的概率非常高。现在,默认情况下,如果我们将阈值设为0.5,那么所有分配概率小于0.5的人将被归类为“不肥胖”,分配概率大于0.5的人将被归类为“肥胖”。但是,我们可以改变这个门槛。如果我把它定为0.3或0.9呢。让我们看看会发生什么。
为了便于理解,我们在样本中抽取了10个人。
要绘制ROC曲线,我们必须绘制(1-特异性),即x轴上的假阳性率和y轴上的敏感性,即真阳性率。
ROC曲线告诉我们,该模型能够很好地区分两种情况(例如,患者是否肥胖)。更好的模型可以准确地区分两者。然而,一个糟糕的模型将很难区分两者。
我们将看到4种不同的场景,其中我们将选择不同的阈值,并将计算ROC曲线对应的x轴和y轴值。
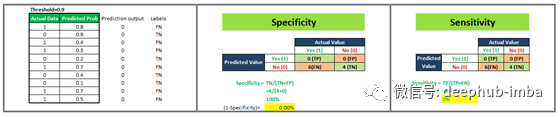
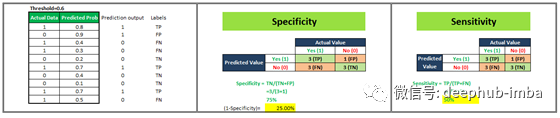

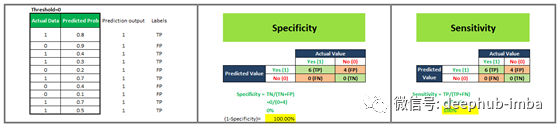
现在,我们有4个数据点,借助这些数据点,我们将绘制ROC曲线,如下所示。
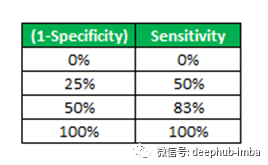
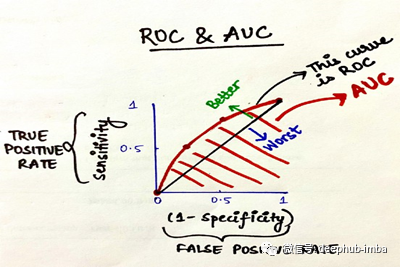
因此,这就是如何为分类模型绘制ROC曲线的方法,通过分配不同的阈值来创建不同的数据点来生成ROC曲线。ROC曲线下的面积称为AUC。AUC越高,你的模型就越好。ROC曲线离中线越远,模型就越好。这就是ROC-AUC如何帮助我们判断分类模型的性能,并为我们提供从多个分类模型中选择一个模型的方法。
PR Curve
在数据主要位于负标签的情况下,ROC-AUC将给我们一个不能很好地代表现实的结果,因为我们主要关注正速率方法,y轴上的TPR和x轴上的FPR。

在这里,您可以看到大多数数据都在负标签下,ROC-AUC不会捕获该信息。在这些场景中,我们转向PR曲线,这只是精确召回曲线。
在PR曲线中,我们将计算并绘制Y轴上的精度和X轴上的调用,实际情况PR曲线正好与ROC曲线相反,所以这里就不再展示了。
作者:Juhi
DeepHub
微信号 : deephub-imba
每日大数据和人工智能的重磅干货
大厂职位内推信息
长按识别二维码关注 ->
好看就点在看!********** **********