IoU已经out了，试试这几个变体:GIoU、DIoU和CIoU介绍与对比分析

你是否曾经训练过一个模型,在评估指标上表现出色,但在实际可视化边界框时,却发现它在许多情况下都失败了?这可能是因为像简单交并比(IoU)这样的标准指标并没有很好地捕捉到你所期望的模型行为。

简单的IoU在当前阶段已经显得有些过时了。

IoU作为一个评估指标可能还算不错,尽管它仍然存在一些问题。但重要的是,其实已经有很多更新、更智能的指标。让我们来看看其中的几个,这样你可能就会重新考虑是否要在模型训练、评估和推理中继续使用IoU这个过时的指标。

为什么IoU很重要

在目标检测任务中,IoU指标实际上贯穿于模型开发的每个阶段:

1. 评估阶段:在评估模型性能时,通常使用IoU指标将预测边界框与真实边界框进行比较。
2. 训练阶段:在优化模型定位能力时,IoU指标的可微分版本常被用作回归损失函数。
3. 推理阶段:在推理过程中,非极大值抑制(NMS)通常被用来处理同一目标被预测出多个边界框的问题。为了解决这个问题,需要比较两个预测框,如果它们的IoU很高,就丢弃置信度较低的那个框。

最近的一些进展,如Yolo-V10和类DETR模型中的"无NMS"训练策略,设法避免了第三种情况。但是第一种和第二种用例在未来可能仍将继续存在。

所以IoU是非常重要的，那么如何能够提高他的效果呢？让我们来看看这些IoU变体!

1、交并比(IoU)

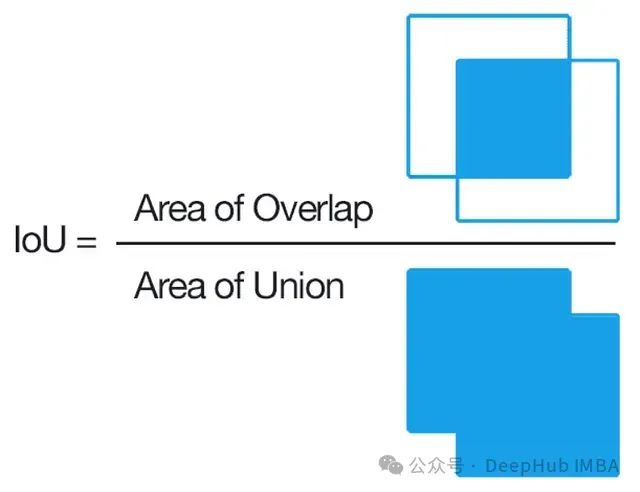
首先从基础开始——所谓的交并比究竟是什么?

这是目标检测领域的首选评估指标。计算两个边界框的IoU时,如果它们有重叠区域,就测量重叠面积,然后除以两个框所覆盖的总面积。

下面是与上图相对应的代码:

 defiou(boxA, boxB):
     xA=max(boxA[0], boxB[0])
     yA=max(boxA[1], boxB[1])
     xB=min(boxA[2], boxB[2])
     yB=min(boxA[3], boxB[3])
 
     # Compute the area of intersection rectangle
     interArea=max(0, xB-xA) *max(0, yB-yA)
 
     # Compute the area of both the prediction and ground-truth rectangles
     boxAArea= (boxA[2] -boxA[0]) * (boxA[3] -boxA[1])
     boxBArea= (boxB[2] -boxB[0]) * (boxB[3] -boxB[1])
 
     # Compute the IoU
     iou=interArea/float(boxAArea+boxBArea-interArea)
 
     returniou

IoU简单且在许多情况下都适用,但它也有缺陷。比如说当两个框很好地重叠时,它的效果不错;但如果两个框完全不重叠呢?那IoU就变成了零!

这种情况在小目标上经常发生,这也是为什么这个指标偏向于大目标的原因。正是IoU缺乏细微表达能力的问题,促使人们开发出了更复杂的变体。

2、广义交并比(GIoU)

当两个框不重叠时,IoU就失效了但如果我们能够度量不重叠的两个框之间的距离呢?

这就是广义IoU(GIoU)。GIoU不仅度量重叠面积,还通过考虑最小外接矩形框的面积来度量两个框之间的距离。

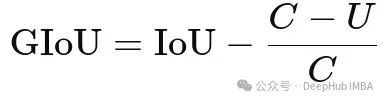
我们用C表示包围两个框的最小矩形框的面积。这样一来,即便是两个框没有重叠(常规IoU为零),GIoU仍然能够提供有价值的反馈,告诉我们预测框在尝试捕获目标方面的效果如何。这有助于我们改进模型训练,使其更适合评估。

GIoU能够提供对模型学习过程更深入的洞察,特别是在训练的早期阶段,因为早就其节点的模型的定位能力往往还很糟糕。

 defgiou(boxA, boxB):
 # Calculate IoU
 iou_value=iou(boxA, boxB)
 
 # Calculate the smallest enclosing box
 xC_min=min(boxA[0], boxB[0])
 yC_min=min(boxA[1], boxB[1])
 xC_max=max(boxA[2], boxB[2])
 yC_max=max(boxA[3], boxB[3])
 
 # Area of the smallest enclosing box
 enclosingArea= (xC_max-xC_min) * (yC_max-yC_min)
 
 # Area of union
 unionArea=boxAArea+boxBArea-interArea
 
 # Calculate GIoU
 giou=iou_value- (enclosingArea-unionArea) /enclosingArea
 
 returngiou

3、距离交并比(DIoU)

为什么我们需要最小外接矩形框呢,难道不能直接度量两个框之间的距离吗?

在训练的初始阶段,使用DIoU作为损失函数可以帮助模型更快地改进定位能力,因为它为不重叠的框提供了更加明确的梯度信号。

DIoU在常规IoU的基础上,额外考虑了两个框中心点之间的欧氏距离

d

:

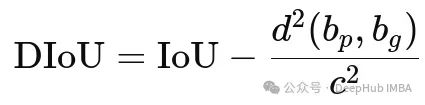
在DIoU的计算中,用

c

的平方(即包围两个框的最小外接矩形框的对角线长度的平方)对距离

d

进行归一化。

DIoU根据预测框中心与真实框中心之间的距离来惩罚预测结果。对于不重叠的两个框,DIoU损失会随着它们之间距离的平方而增大,而GIoU损失则有一定的饱和趋势。

这使得模型在处理不重叠框时能够更快地学习。但是,DIoU损失有时会导致梯度信号过于极端,从而导致权重更新幅度过大,尤其是在使用一些带噪声的标注分配算法(如DETR类模型中的匈牙利算法)时。

DIoU的另一个缺点在于,它过于关注两个框中心的距离,而忽略了框本身形状的差异。

究竟哪种损失函数最适合你呢,还是取决于具体的任务、数据和训练设置。建议都试一试,看看DIoU是否能给你带来更好的效果。

 importnumpyasnp
 
 defdiou(boxA, boxB):
     # Calculate IoU
     iou_value=iou(boxA, boxB)
 
     # Center of boxA and boxB
     centerA= [(boxA[0] +boxA[2]) /2, (boxA[1] +boxA[3]) /2]
     centerB= [(boxB[0] +boxB[2]) /2, (boxB[1] +boxB[3]) /2]
 
     # Distance between the centers
     center_distance=np.linalg.norm(np.array(centerA) -np.array(centerB))
 
     # Diagonal distance of the enclosing box
     xC_min=min(boxA[0], boxB[0])
     yC_min=min(boxA[1], boxB[1])
     xC_max=max(boxA[2], boxB[2])
     yC_max=max(boxA[3], boxB[3])
     diagonal_distance=np.linalg.norm([xC_max-xC_min, yC_max-yC_min])
 
     # Calculate DIoU
     diou=iou_value- (center_distance**2) / (diagonal_distance**2)
 
     returndiou

4、完全交并比(CIoU)

我们如何在DIoU的基础上同时优化两个框的形状差异呢?这就引出了CIoU。

这个"超级损失函数"集成了前面提到的各种IoU变体的优点。它类似于DIoU,但额外引入了一项用于惩罚长宽比差异的项。可以把CIoU看作是边界框回归任务的"终极Boss"!

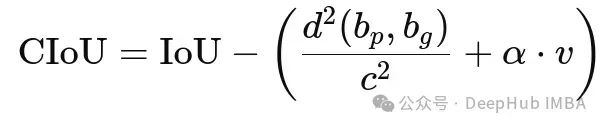
CIoU的公式,其中引入了两个新的项:

α

和

v

。

v

项度量了两个框的长宽比差异。它的定义相对复杂,但可以类比为一种广义上的欧氏距离。

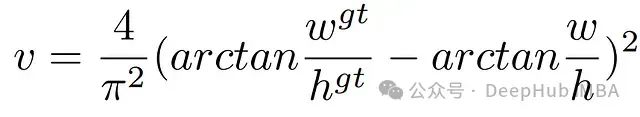
α

是一个权重项,用于平衡IoU项和长宽比差异项。当预测框与真实框的重合度很低时,

α

会趋近于0,此时CIoU退化为DIoU;而当重合度较高时,

α

会趋近于1,此时CIoU会更多地考虑两个框的形状差异。

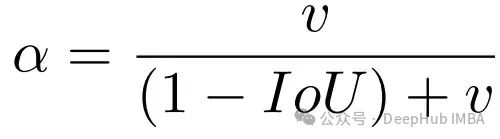
CIoU可能是当前最前沿的目标检测系统中使用的最复杂的IoU变体。它同时考虑了:

1. 两个框中心点之间的距离(像DIoU一样)
2. 两个框的形状/大小的相似程度
3. 并通过权重项α来平衡二者

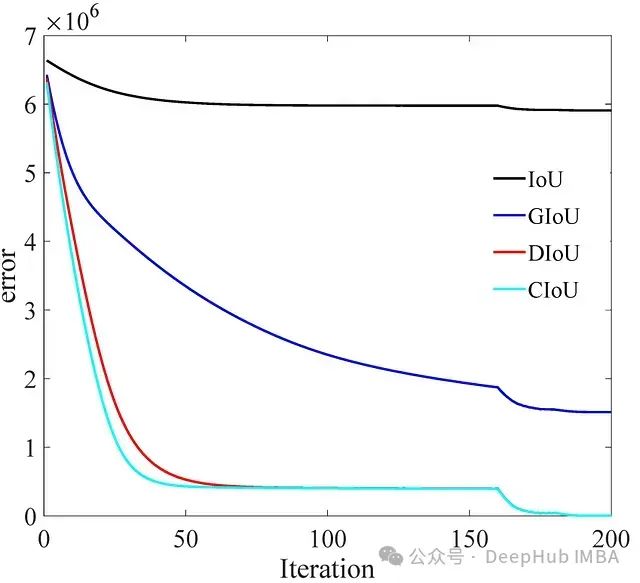
使用CIoU确实能够给我带来一些性能提升,但相比DIoU而言,提升幅度并不算太大。这也与最初提出DIoU和CIoU的论文《Distance-IoU损失》的实验结果基本一致。下图展示了他们在一个实验中使用不同IoU变体所得到的收敛曲线。

需要注意的是,为了提高训练稳定性,对于定位很差的预测框,我们通常将

α

项设为0。这样可以保证模型先专注于缩小两个框的距离,而不去过早地优化形状差异。

下面是一个PyTorch实现的CIoU损失函数:

 defciou(boxA, boxB):
     # Calculate DIoU
     diou_value=diou(boxA, boxB)
     iou_value=iou(boxA, boxB)
 
     # Width and height of the boxes
     widthA, heightA=boxA[2] -boxA[0], boxA[3] -boxA[1]
     widthB, heightB=boxB[2] -boxB[0], boxB[3] -boxB[1]
 
     # Aspect ratio penalty
     v= (4/ (np.pi**2)) *np.power(np.arctan(widthA/heightA) -np.arctan(widthB/heightB), 2)
     alpha=v/ ((1-iou_value) +v) ifiou_value>0.5else0
 
     # CIoU calculation
     ciou=diou_value+alpha*v
 
     returnciou

总结

GIoU、DIoU和CIoU这三个变体都有各自的独到之处,它们在一定程度上弥补了普通IoU在处理不重叠、距离较远或形状差异较大的边界框时的不足。

这些新的指标不仅仅给出一个量化的分数,它们的各项组成部分还能告诉我们,预测结果好坏的原因究竟是什么。

虽然本文主要聚焦在训练阶段,但请注意,这些指标实际上可以用于所有三个场景:训练、评估和推理。所以建议在所有场合都使用CIoU,但在评估时,可能还需要一些时间来建立对其数值的直观理解。

当然最后还是我们一直说的那句话到底应该使用哪种IoU变体组合,还是要看你自己的实际情况!每个都试一试，一定不会有错的。

作者：Benjamin Bodner