不同数据类型的相关性分析总结

    在进行数据建模之前，我们一般会进行数据探索和描述性分析，发现数据规律及数据之间的相关性，本文主要从检验方法和可视化图形两个方面对不同数据类型的相关性分析方法进行总结，以加强对数据的了解和认识，为建模打下基础。

一、不同数据类型的相关性总结

自变量、因变量数据类型检验方法可视化图形连续型&连续型相关系数散点图（大数据量不建议使用）连续型&离散型(二分类)t检验/z检验分组箱线图、logit图（因变量为二分类，自变量为连续型）离散型(多分类)&分类型方差分析分组箱线图离散型&离散型卡方检验堆叠图、改进的堆叠图

二、不同数据类型的相关性案例

2.1 连续变量 与 连续变量

以信用卡申请及消费信息数据源为例，下载连接如下：线性回归建模及模型诊断数据集--creditcard_exp.csv_线性回归数据集-数据挖掘文档类资源-CSDN下载数据源中目标变量为avg_exp（月均消费金额），其余为自变量，首先筛选Acc=1（已开卡的用户数据，已开卡的用户才有消费），观察连续变量Age（申请人年龄）、Income（年收入）、dist_home_val（所住小区房屋均价）、dist_avg_income（当地人均收入）、high_avg（高出当地平均收入）和目标变量avg_exp（月均消费金额）之间的相关性。

2.1.1 可视化图形--散点图

因本数据集的数据量不大，可首先通过散点图可视化来看所有变量间的相关程度：

%matplotlib inline
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import stats 
import statsmodels.api as sm
import statsmodels.formula.api as smf

# 导入案例中的数据
df2 = pd.read_csv('./data/creditcard_exp.csv')
df2 = df2[df2['Acc'] == 1]  # 筛选已开卡数据
df2 = df2.astype({'avg_exp': 'float64', 'avg_exp_ln': 'float64'}) # 修改字段数据类型

# 连续变量， 共6个
cons_df = df2[['avg_exp', 'Age', 'Income', 'dist_home_val', 'dist_avg_income', 'high_avg']]

# 绘制两两间的散点图
fig = plt.figure(figsize = (20, 10))
axs = fig.subplots(6, 6)
for i in range(6):
    for j in range(6):
        axs[i, j].scatter(cons_df.iloc[:, i], cons_df.iloc[:, j])

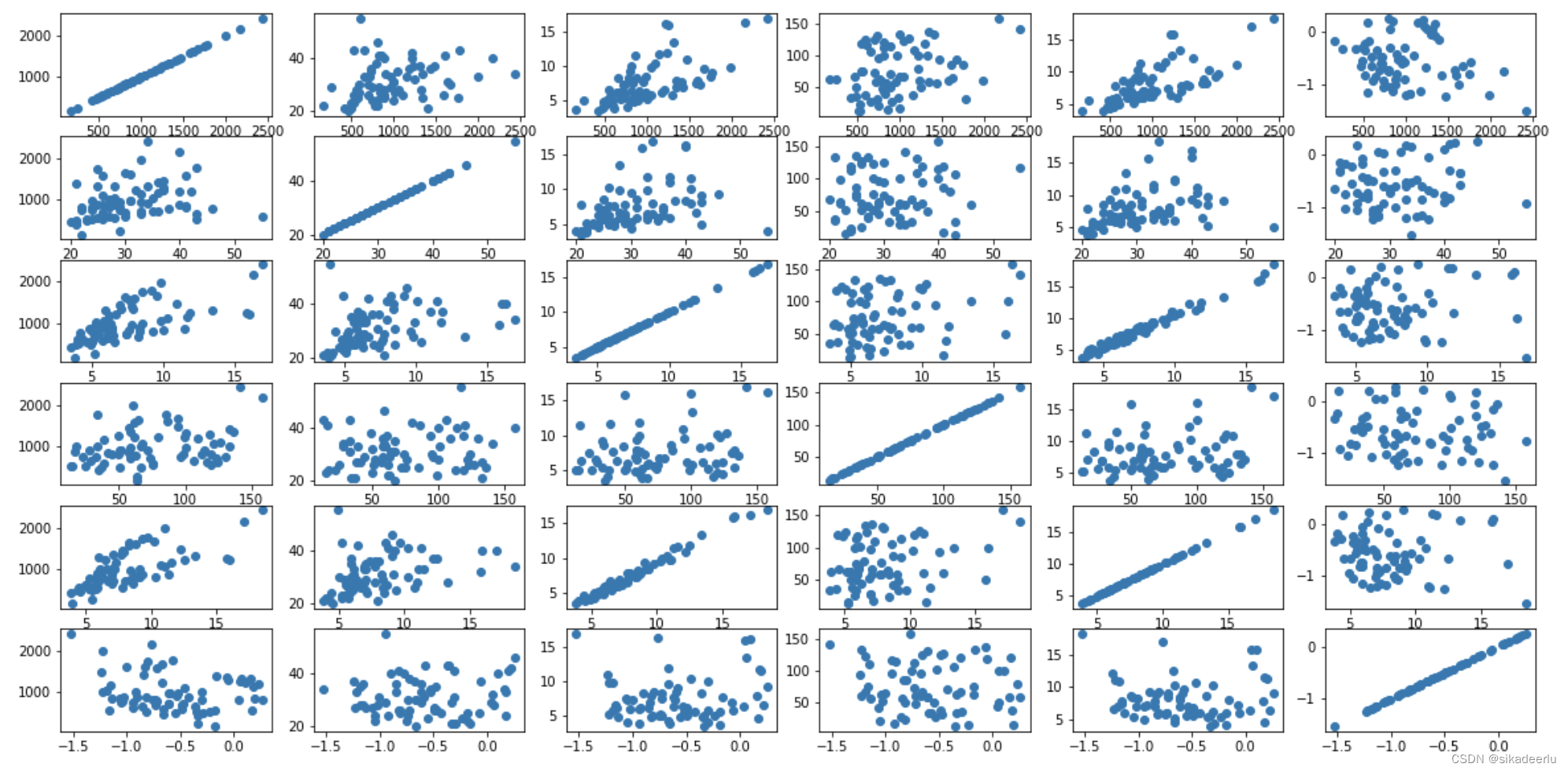
上图中按行看是按以上连续变量，每个变量与其他变量的散点图，因变量avg_exp为第一个，只观察第一行即可。与avg_exp线性关系较明显的是Income（年收入）、 dist_avg_income（当地人均收入）。

2.1.2 检验方法--相关系数

接着通过相关系数看其相关程度：

cons_df.corr()

同样观察第一行，avg_exp和Income的相关系数为0.67，与dist_avg_income的相关系数为0.70，这两者的相关性较强，因此如果预测用户开卡后的月均消费水平，这两个变量会有较好的预测能力。

2.2 连续因变量 与 二分类自变量

使用上小节信用卡申请及消费信息数据数据源中，观察Ownrent（是否自有住房）的月均信用卡消费水平是否有显著差异。

2.2.1 可视化图形--箱线图

首先用箱线图查看是否自有住房的月均信用卡消费的分布差异，可以看出自有住房的消费水平明显高于非自有住房。

import seaborn as sns

sns.boxplot(df2['Ownrent'], df2['avg_exp']) # 画箱线图

2.2.2 检验方法--t检验

接着用t检验（样本量较小可用t检验，本案例中Ownrent为1的有27条，为0的有43条）对其差异进行显著性检验，其p值为0.01 < 0.05，故认为是否自有住房的月均消费水平是显著的。

import scipy.stats as st   # 引入scipy.stats进行t检验

st.ttest_ind(df2[df2['Ownrent'] == 0]['avg_exp'], df2[df2['Ownrent'] == 1]['avg_exp'])

2.3 连续自变量 与 二分类因变量

连续自变量和二分类因变量的相关性分析可以套用2.2章节中的方法进行，除此之外，在可视化图形方面，可以用Logit图来更近一步的查看连续自变量的变化对因变量的影响。本案例为车辆出险保险理赔数据，Loss为车辆是否出险，可将其处理为0-1变量，其余变量为车主、汽车特征。下载链接如下：不同数据类型的相关性分析总结数据集1--auto_ins.csv-机器学习文档类资源-CSDN下载

分析车主驾龄Age和是否出险is_loss之间的相关性

2.3.1 可视化图形--箱线图

df3 = pd.read_csv('./data/auto_ins.csv', encoding = 'gbk')
df3['is_loss'] = [1 if i > 0 else 0 for i in df3['Loss']]  # 目标变量

sns.boxplot(df3['is_loss'], df3['Age']) 

从箱线图结果来看，出险与否的年龄分布无明显差异

2.3.2 检验方法--z检验

sw.ztest(df3[df3['is_loss'] == 0]['Age'], df3[df3['is_loss'] == 1]['Age'])

从z检验结果的p值0.21 > 0.05可知，两者之间的相关性未通过显著性检验。

2.3.3 可视化图形--Logit图

上述z检验未通过，说明其相关性不强，但仅通过检验并不能告诉我们不同年龄段的出险概率的变化情况，Logit图能够进一步观察自变量的变化对因变量的影响，如下是参考代码

# 画logit图， 参数df为数据集，col为连续变量字段名, target_name为目标变量字段名
def plot_distribute_fig(df, col, target_name):
    # 首先对连续特征变量进行等频分箱
    out, bins = pd.qcut(df[col], 20 ,duplicates='drop', retbins = True)
    new_col = col + '_cut'
    df[new_col] = out
    
    bad_ind_0 = df[df[target_name] == 0][target_name].count()   # 目标变量为0的总数
    bad_ind_1 = df[df[target_name] == 1][target_name].count()   # 目标变量为1的总数

    # 计算分箱中目标变量分布
    bad_ind_c_0 = df[df[target_name] == 0].groupby(new_col).count()[target_name] # 分箱中为0的个数
    bad_ind_c_1 = df[df[target_name] == 1].groupby(new_col).count()[target_name] # 分箱中为1的个数
    bad_ind_c_t = df.groupby(new_col).count()[target_name] # 分箱中的总数
    bad_ind_c_1_p = bad_ind_c_1/bad_ind_1 # 分箱中目标变量为1的占比
    
    # 将其存入新变量中
    woe_df = pd.DataFrame({new_col + '_0': bad_ind_c_0, new_col + '_1': bad_ind_c_1, new_col + '_t': bad_ind_c_t, new_col + '_1_p': bad_ind_c_1_p})

    # 左轴绘制连续变量分箱的个数
    ax1.bar(x, woe_df[new_col + '_t'], label = 'nums of bins')
    ax1.set_xticks(x, woe_df.index)   # 设置坐标轴标签
    
    # 右轴绘制该分箱中目标变量为1的占比
    ax2 = ax1.twinx()   # 设置双轴
    ax2.plot(x, bad_ind_c_1_p, color = 'red', label = 'bad pct of bins')
    fig.legend(loc = 1, bbox_to_anchor=(1,1), bbox_transform=ax1.transAxes) # 需加属性，否则图例会出界
    ax2.set_title('nums and bad pct of per bins')

    return woe_df

woe_df = plot_distribute_fig(df3, 'Age', 'is_loss')

通过Logit可以看出，随着车主驾龄的增加，出险的概率在下降。

2.4 多分类自变量 与 连续目标变量

继续使用2.1 章节中的数据集为例，来看不同教育水平edu_class的月均消费水平avg_exp是否有显著差异，可视化分析上依然可以用分组箱线图来查看

2.4.1 可视化图形--分组箱线图

sns.boxplot(df2['edu_class'], df2['avg_exp'])

从箱线图中可以看到不同教育水平的消费水平之间有显著差异

2.4.2 检验方法--方差分析

多分类变量和连续变量之间的相关性检验可以通过两两之间的t/z检验进行，但较为繁琐。一般使用方差分析进行，方差分析能够更高效的检验不同分组之间的显著性差异，可通过单因素方差分析的f检验进行，也可通过建立线性回归模型并对其进行方差分析，具体代码如下。

（1）单因素方差分析

# 单因素方差分析
avg_exp_arr = []
for i in range(4):
    avg_exp_arr.append(df2[df2['edu_class'] == i]['avg_exp'])
    
stats.f_oneway(*avg_exp_arr)  # 模块来自 from scipy import stats 

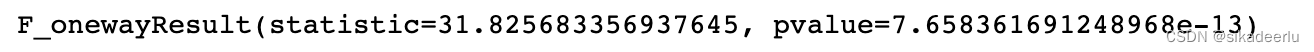（2）建立线性回归模型并进行方差分析

lr = smf.ols(formula = 'avg_exp~C(edu_class)', data = df2).fit() # 建立线性回归模型
df2_anova = sm.stats.anova_lm(lr, typ = 1) # 对模型进行方差分析
df2_anova

可以看到其结果是一样的，即认为不同教育水平的信用卡消费有显著差异。（该方法也可进行多因素方差分析）

2.5 分类变量 与 分类变量

该案例使用2.3章节中的车辆出险保险理赔的数据源，其特征变量为性别，目标变量为是否出险，分析两者之间的相关性。

2.5.1 可视化图形--堆叠图

首先用堆叠图，来看不同性别的出险分布情况

df3_cross = pd.crosstab(df3['Gender'], df3['is_loss'], margins = True) # 列联表
df3_cross_p = df3_cross.apply(lambda x: x/x['All'], axis = 1) # 计算占比
print(df3_cross_p)
df3_cross_p.iloc[0:2, 0:2].plot(kind = 'bar', stacked = True) # 画出堆叠图

2.5.2 可视化图形--改进堆叠图

从上堆叠图中可看到不同性别的出险概率有差异，但不能看出男女两者的样本量差异，如下是改进的堆叠图，能直观的看出男女分布及其出现概率情况。

def plot_stacked(data_raw):
    # 计算占比
    data_raw_1 = data_raw.div(data_raw.sum(axis = 1), axis = 'index')
    
    y_0_p = data_raw_1.iloc[:,0]   # 各分类变量中 目标变量为0的 占比
    y_1_p = data_raw_1.iloc[:,1]   # 各分类变量中 目标变量为1的 占比
    
    # 获取每个分类变量在整体中的占比
    data_raw['pct'] = data_raw.sum(axis = 1)/data_raw.sum(axis = 1).sum()
    
    x = data_raw['pct']   # 每根柱子的坐标

    plt.figure(figsize = (8, 6))
    plt.bar(x, y_0_p, color = 'royalblue', width = x, label = '0')  # 每根柱子的第一截
    plt.bar(x, y_1_p, bottom = y_0_p, color = 'darkorange', label = '1', width = x)  # 每根柱子的第二截

    plt.xticks(x, ['0', '1'])

    plt.legend(loc='best', title = 'is_loss')
    plt.show()

plot_stacked(pd.crosstab(df3['Gender'], df3['is_loss']))

2.5.3 检验方法--卡方检验

分类变量的检验方法可通过卡方检验进行，如下是参考代码。

stats.chi2_contingency(df3_cross.iloc[:2, :2])

通过上图可以看出卡方检验的p值为0.00018 < 0.05，即认为不同性别间的出险差异是显著的。两分类变量的相关性程度可用Cramer's V系数来度量，其计算公式如下：

是卡方值，为列联表的总频数即样本量，为行数，为列数，该值越大说明相关性越强，否则越小(参考自贾俊平老师第三版统计学p204-205页)。