随机变量的分布函数

随机变量的分布函数，是我们在概率论中经常会遇到的概念。它是衡量一个随机变量在某个取值范围内出现的概率密度累积函数。在本篇博客中，我们将详细讨论随机变量的分布函数的定义、性质以及应用。

一、分布函数

概念

首先，我们看一下随机变量的分布函数的定义。对于任意一个随机变量 X，其分布函数是指 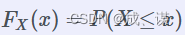，即随机变量 X取值小于等于 x 的概率。例如，

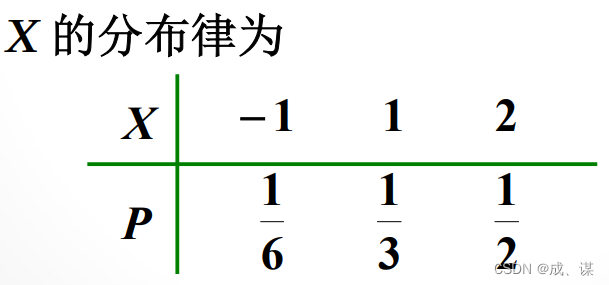
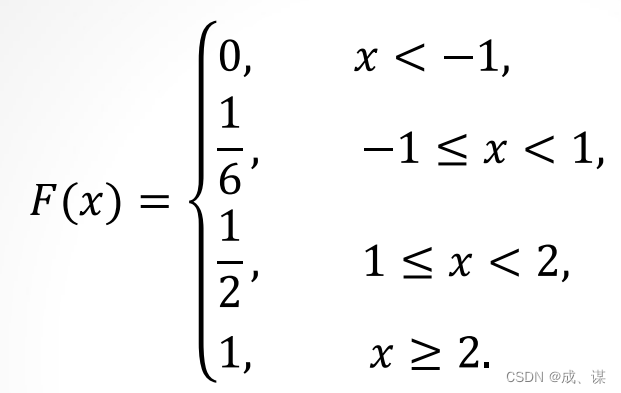
随机变量分布函数的性质如下：

1. 随机变量分布函数是单调不减的。
2. 随机变量分布函数在 x=−∞ 处为 0，在 x=+∞处为 1。
3. 随机变量的概率密度函数与分布函数的关系可以表示为 P(a<X<b)=(b)−(a)。
4. 是右连续的，即 .

除了以上这些基本概念和性质，随机变量的分布函数还有许多应用。

如在统计学上，随机变量的分布函数可以用于描述一个样本的分布情况。例如，如果我们想知道一个班级的学生成绩分布情况，我们可以将成绩看作是一个随机变量，并求出该随机变量的分布函数。通过分析分布函数的形状和特征，我们可以了解到学生成绩的平均水平、优秀和不合格的比例等信息。

总之，随机变量的分布函数是概率论中最基本的概念之一，应用范围广泛。通过对分布函数的研究和掌握，我们可以更好地理解和描述随机事件的规律和特征，从而更加准确地进行决策和预测。

二、概率密度函数

定义

性质

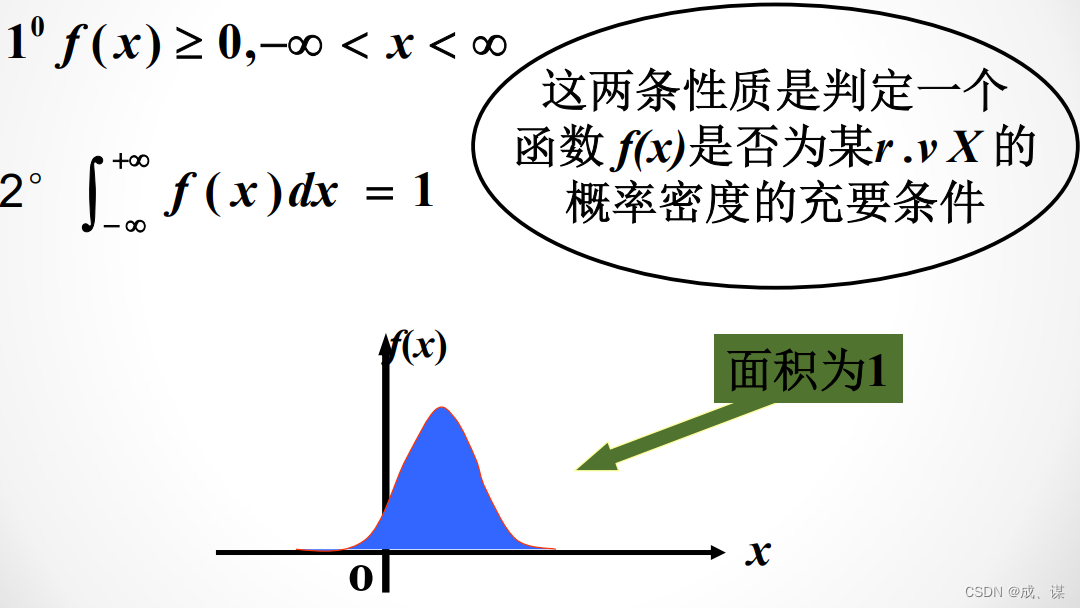
注意:密度函数f(不是r.v.X在x点取值的概率.但是，f(x)越大，则X取a附近的值的概率就越大,即反映了概率集中在该点附近的程度.