🤵 Author :Horizon Max
✨ 编程技巧篇:各种操作小结
🎇 机器视觉篇:会变魔术 OpenCV
💥 深度学习篇:简单入门 PyTorch
🏆 神经网络篇:经典网络模型
💻 算法篇:再忙也别忘了 LeetCode
[ 注意力机制 ] 经典网络模型2——CBAM 详解与复现
🚀 Convolutional Block Attention Module
Convolutional Block Attention Module 简称
CBAM
,Sanghyun等人于2018年提出的一种新的 卷积注意力模块 ;
创新提出了 通道注意力与空间注意力融合 的注意力机制 ;
对前馈卷积神经网络 是一个 简单而有效的 注意力模块 ;
因为它的 轻量级和通用性 ,可以 无缝集成到任何CNN网络 当中 ;
作者实验表明,不同的模型在 分类和检测性能 上都有持续的提高 ;
🔗 论文地址:CBAM: Convolutional Block Attention Module
🚀 CBAM 详解
🎨 背景知识
为提高
CNN性能
,最近的研究主要研究了网络的三个重要因素:
depth(深度)
,
width(宽度)
,
cardinality(基数)
从20世纪90年代 LeNet 网络的提出,网络的
深度
不断增加;
后来 VGG 网络表明,
相同形状的块堆叠
效果良好;
GoogLeNet 网络的提出,提出
宽度
也是提高模型性能的另一个重要因素;
同样的,ResNet 将
残差块
以相同拓扑与跳跃式连接堆叠在一起,构建了一个非常深的架构,达到了不错的效果;
Xception 和 ResNeXt 网络表明,增加网络
基数
不仅减少了参数量,而且比另 两个因素(深度和宽度) 具有更强的表示能力;
除了这些因素之外,作者还研究了网络设计的另一个方面——
注意力
;
“注意力” 也是 人类视觉系统 的一个很有趣的地方 ;
通过注意力机制来增加网络的表征力:关注重要特征,抑制不必要特征 ;
卷积运算是通过将 跨通道信息和空间信息混合 在一起来提取信息特征的 ;
因此提出了 CBAM 来强调通道轴和空间轴这两个主要维度上的有意义特征 ;
并对此依次应用了
Channel Attention Module (通道注意模块)
和
Spatial Attention Module (空间注意模块)
;
Convolutional Block Attention Module
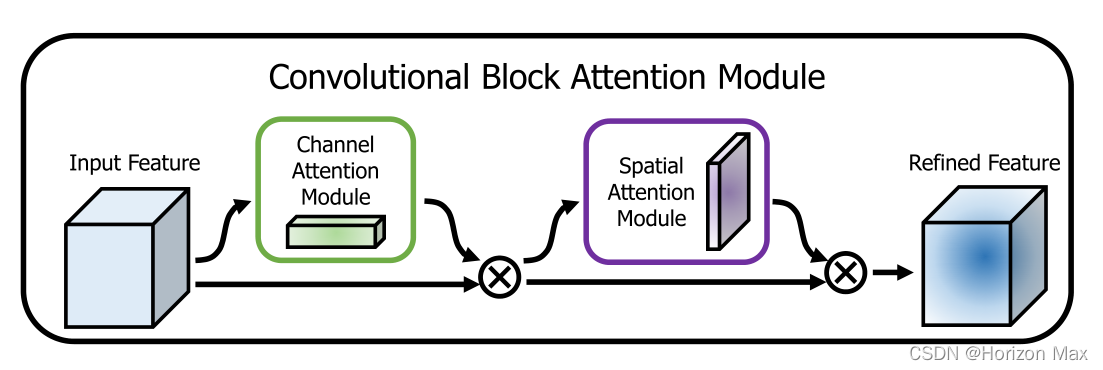
🎨 论文贡献
(1)提出了一个简单而有效的注意力模块(CBAM),可以广泛应用于提高 CNN 的表示能力 ;
(2)通过广泛的消融研究来验证我们的注意力模块的有效性 ;
(3)通过插入轻量级模块(CBAM),验证了各种网络的性能在多个基准(ImageNet-1K、MS COCO和VOC 2007)上都得到了极大的提高;
假设
输入特征图
为 : F ∈ R CxHxW ;
利用
CBAM
依此推导出
一维通道注意图
: Mc ∈ R Cx1x1 和
二维空间注意图
: Ms ∈ R 1xHxW ;
总的注意过程可以概括为 :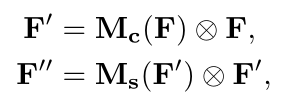
🎨 Convolutional Block Attention Module

🚩 Channel Attention Module
利用
特征间的通道关系
来生成通道注意图 ;
由于feature map的每个channel都被认为是
一个feature检测器
,因此 channel 的注意力集中在
给定输入图像的 "什么" 是有意义的
;
为了有效地计算通道注意力,采用
压缩输入特征映射的空间维度
的方法 ;
文中同时使用
AvgPool (平均池化)
和
MaxPool (最大池化)
的方法,并证明了这种做法比单独使用一种池化方法更具有表征力;
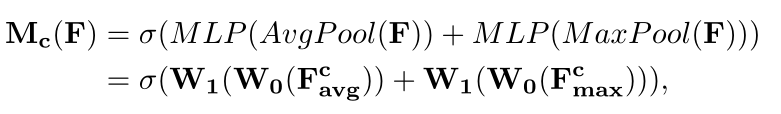
式中,σ 为
sigmoid
函数 ,W0 ∈ RC/r×C ,W1 ∈ RC×C/r ,MLP的权重 W0 和 W1 共享,在W0 前是
ReLU
激活函数 ;
🚩 Spatial Attention Module
利用
特征间的空间关系
生成空间注意图 ;
与通道注意模块不同的是,空间注意模块关注的是
信息部分 "在哪里"
,作为通道注意模块的补充 ;
为了计算空间注意力,首先沿着通道轴应用
平均池化和最大池化
操作,并将它们连接起来以生成一个有效的
特征描述符
;
使用两个池化操作聚合一个feature map的通道信息,生成两个2D maps :
Fsavg ∈ R1×H×W 和 Fsmax ∈ R1×H×W ;
每个都表示通道的
平均池化特性
和
最大池化特性
,然后利用一个标准的卷积层进行连接和卷积操作,得到二维空间注意力图 ;
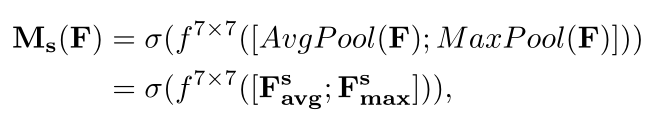
式中,σ 为
sigmoid
函数 ,f 7x7 为 7 x 7 大小的卷积核 ;
🚩 CBAM 的应用
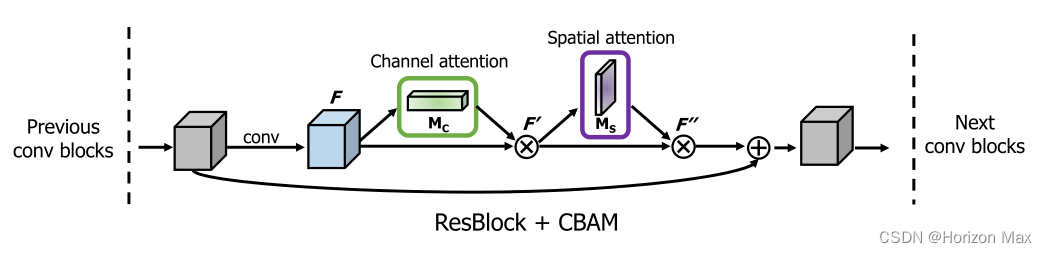
以上是将
CBAM
结合
ResBlock
应用于ResNet中 ;
两个模块可以以并行或顺序的方式放置,实验测试发现
顺序排列
比
并行排列
有更好的结果 ;
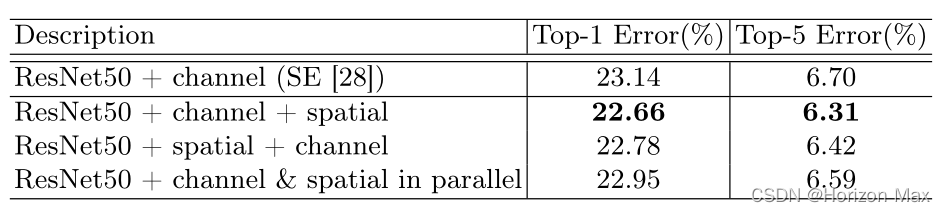
最后,分别使用 ResNet50 、ResNet50+SENet 、ResNet50+CBAM 进行实验得到可视化结果 :
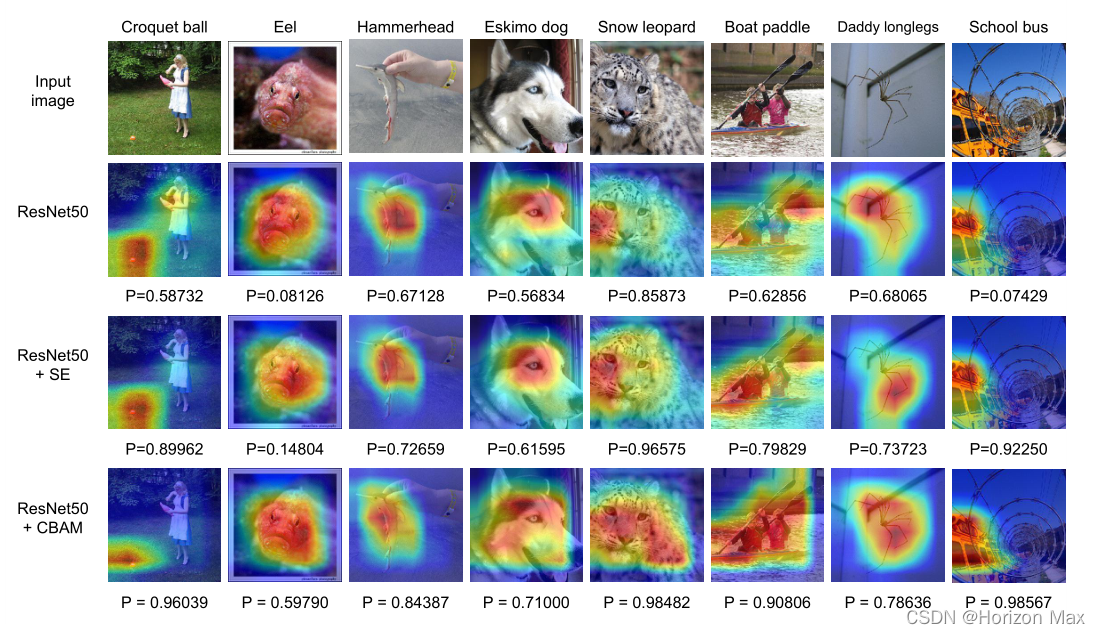
实验表明 CBAM 性能超越了 SENet
🚀 CBAM 复现
这里实现的是
CBAM-ResNet
系列网络 :
# Here is the code :import torch
import torch.nn as nn
import torch.nn.functional as F
from torchinfo import summary
classChannelAttention(nn.Module):# Channel Attention Moduledef__init__(self, in_planes):super(ChannelAttention, self).__init__()
self.avg_pool = nn.AdaptiveAvgPool2d(1)
self.max_pool = nn.AdaptiveMaxPool2d(1)
self.fc1 = nn.Conv2d(in_planes, in_planes //16, kernel_size=1, bias=False)
self.relu = nn.ReLU()
self.fc2 = nn.Conv2d(in_planes //16, in_planes, kernel_size=1, bias=False)
self.sigmoid = nn.Sigmoid()defforward(self, x):
avg_out = self.avg_pool(x)
avg_out = self.fc1(avg_out)
avg_out = self.relu(avg_out)
avg_out = self.fc2(avg_out)
max_out = self.max_pool(x)
max_out = self.fc1(max_out)
max_out = self.relu(max_out)
max_out = self.fc2(max_out)
out = avg_out + max_out
out = self.sigmoid(out)return out
classSpatialAttention(nn.Module):# Spatial Attention Moduledef__init__(self):super(SpatialAttention, self).__init__()
self.conv1 = nn.Conv2d(2,1, kernel_size=7, padding=3, bias=False)
self.sigmoid = nn.Sigmoid()defforward(self, x):
avg_out = torch.mean(x, dim=1, keepdim=True)
max_out, _ = torch.max(x, dim=1, keepdim=True)
out = torch.cat([avg_out, max_out], dim=1)
out = self.conv1(out)
out = self.sigmoid(out)return out
classBasicBlock(nn.Module):# 左侧的 residual block 结构(18-layer、34-layer)
expansion =1def__init__(self, in_planes, planes, stride=1):# 两层卷积 Conv2d + Shutcutssuper(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3,
stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3,
stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.channel = ChannelAttention(self.expansion*planes)# Channel Attention Module
self.spatial = SpatialAttention()# Spatial Attention Module
self.shortcut = nn.Sequential()if stride !=1or in_planes != self.expansion*planes:# Shutcuts用于构建 Conv Block 和 Identity Block
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion*planes,
kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion*planes))defforward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
CBAM_Cout = self.channel(out)
out = out * CBAM_Cout
CBAM_Sout = self.spatial(out)
out = out * CBAM_Sout
out += self.shortcut(x)
out = F.relu(out)return out
classBottleneck(nn.Module):# 右侧的 residual block 结构(50-layer、101-layer、152-layer)
expansion =4def__init__(self, in_planes, planes, stride=1):# 三层卷积 Conv2d + Shutcutssuper(Bottleneck, self).__init__()
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3,
stride=stride, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.conv3 = nn.Conv2d(planes, self.expansion*planes,
kernel_size=1, bias=False)
self.bn3 = nn.BatchNorm2d(self.expansion*planes)
self.channel = ChannelAttention(self.expansion*planes)# Channel Attention Module
self.spatial = SpatialAttention()# Spatial Attention Module
self.shortcut = nn.Sequential()if stride !=1or in_planes != self.expansion*planes:# Shutcuts用于构建 Conv Block 和 Identity Block
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion*planes,
kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion*planes))defforward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = F.relu(self.bn2(self.conv2(out)))
out = self.bn3(self.conv3(out))
CBAM_Cout = self.channel(out)
out = out * CBAM_Cout
CBAM_Sout = self.spatial(out)
out = out * CBAM_Sout
out += self.shortcut(x)
out = F.relu(out)return out
classCBAM_ResNet(nn.Module):def__init__(self, block, num_blocks, num_classes=1000):super(CBAM_ResNet, self).__init__()
self.in_planes =64
self.conv1 = nn.Conv2d(3,64, kernel_size=3,
stride=1, padding=1, bias=False)# conv1
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(block,64, num_blocks[0], stride=1)# conv2_x
self.layer2 = self._make_layer(block,128, num_blocks[1], stride=2)# conv3_x
self.layer3 = self._make_layer(block,256, num_blocks[2], stride=2)# conv4_x
self.layer4 = self._make_layer(block,512, num_blocks[3], stride=2)# conv5_x
self.avgpool = nn.AdaptiveAvgPool2d((1,1))
self.linear = nn.Linear(512* block.expansion, num_classes)def_make_layer(self, block, planes, num_blocks, stride):
strides =[stride]+[1]*(num_blocks-1)
layers =[]for stride in strides:
layers.append(block(self.in_planes, planes, stride))
self.in_planes = planes * block.expansion
return nn.Sequential(*layers)defforward(self, x):
x = F.relu(self.bn1(self.conv1(x)))
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
x = self.avgpool(x)
x = torch.flatten(x,1)
out = self.linear(x)return out
defCBAM_ResNet18():return CBAM_ResNet(BasicBlock,[2,2,2,2])defCBAM_ResNet34():return CBAM_ResNet(BasicBlock,[3,4,6,3])defCBAM_ResNet50():return CBAM_ResNet(Bottleneck,[3,4,6,3])defCBAM_ResNet101():return CBAM_ResNet(Bottleneck,[3,4,23,3])defCBAM_ResNet152():return CBAM_ResNet(Bottleneck,[3,8,36,3])deftest():
net = CBAM_ResNet50()
y = net(torch.randn(1,3,224,224))print(y.size())
summary(net,(1,3,224,224))if __name__ =='__main__':
test()
输出结果:
torch.Size([1,1000])===============================================================================================
Layer (type:depth-idx) Output Shape Param #===============================================================================================
CBAM_ResNet ----
├─Conv2d:1-1[1,64,224,224]1,728
├─BatchNorm2d:1-2[1,64,224,224]128
├─Sequential:1-3[1,256,224,224]--
│ └─Bottleneck:2-1[1,256,224,224]--
│ │ └─Conv2d:3-1[1,64,224,224]4,096
│ │ └─BatchNorm2d:3-2[1,64,224,224]128
│ │ └─Conv2d:3-3[1,64,224,224]36,864
│ │ └─BatchNorm2d:3-4[1,64,224,224]128
│ │ └─Conv2d:3-5[1,256,224,224]16,384
│ │ └─BatchNorm2d:3-6[1,256,224,224]512
│ │ └─ChannelAttention:3-7[1,256,1,1]8,192
│ │ └─SpatialAttention:3-8[1,1,1,1]98
│ │ └─Sequential:3-9[1,256,224,224]16,896
│ └─Bottleneck:2-2[1,256,224,224]--
│ │ └─Conv2d:3-10[1,64,224,224]16,384
│ │ └─BatchNorm2d:3-11[1,64,224,224]128
│ │ └─Conv2d:3-12[1,64,224,224]36,864
│ │ └─BatchNorm2d:3-13[1,64,224,224]128
│ │ └─Conv2d:3-14[1,256,224,224]16,384
│ │ └─BatchNorm2d:3-15[1,256,224,224]512
│ │ └─ChannelAttention:3-16[1,256,1,1]8,192
│ │ └─SpatialAttention:3-17[1,1,1,1]98
│ │ └─Sequential:3-18[1,256,224,224]--
│ └─Bottleneck:2-3[1,256,224,224]--
│ │ └─Conv2d:3-19[1,64,224,224]16,384
│ │ └─BatchNorm2d:3-20[1,64,224,224]128
│ │ └─Conv2d:3-21[1,64,224,224]36,864
│ │ └─BatchNorm2d:3-22[1,64,224,224]128
│ │ └─Conv2d:3-23[1,256,224,224]16,384
│ │ └─BatchNorm2d:3-24[1,256,224,224]512
│ │ └─ChannelAttention:3-25[1,256,1,1]8,192
│ │ └─SpatialAttention:3-26[1,1,1,1]98
│ │ └─Sequential:3-27[1,256,224,224]--
├─Sequential:1-4[1,512,112,112]--
│ └─Bottleneck:2-4[1,512,112,112]--
│ │ └─Conv2d:3-28[1,128,224,224]32,768
│ │ └─BatchNorm2d:3-29[1,128,224,224]256
│ │ └─Conv2d:3-30[1,128,112,112]147,456
│ │ └─BatchNorm2d:3-31[1,128,112,112]256
│ │ └─Conv2d:3-32[1,512,112,112]65,536
│ │ └─BatchNorm2d:3-33[1,512,112,112]1,024
│ │ └─ChannelAttention:3-34[1,512,1,1]32,768
│ │ └─SpatialAttention:3-35[1,1,1,1]98
│ │ └─Sequential:3-36[1,512,112,112]132,096
│ └─Bottleneck:2-5[1,512,112,112]--
│ │ └─Conv2d:3-37[1,128,112,112]65,536
│ │ └─BatchNorm2d:3-38[1,128,112,112]256
│ │ └─Conv2d:3-39[1,128,112,112]147,456
│ │ └─BatchNorm2d:3-40[1,128,112,112]256
│ │ └─Conv2d:3-41[1,512,112,112]65,536
│ │ └─BatchNorm2d:3-42[1,512,112,112]1,024
│ │ └─ChannelAttention:3-43[1,512,1,1]32,768
│ │ └─SpatialAttention:3-44[1,1,1,1]98
│ │ └─Sequential:3-45[1,512,112,112]--
│ └─Bottleneck:2-6[1,512,112,112]--
│ │ └─Conv2d:3-46[1,128,112,112]65,536
│ │ └─BatchNorm2d:3-47[1,128,112,112]256
│ │ └─Conv2d:3-48[1,128,112,112]147,456
│ │ └─BatchNorm2d:3-49[1,128,112,112]256
│ │ └─Conv2d:3-50[1,512,112,112]65,536
│ │ └─BatchNorm2d:3-51[1,512,112,112]1,024
│ │ └─ChannelAttention:3-52[1,512,1,1]32,768
│ │ └─SpatialAttention:3-53[1,1,1,1]98
│ │ └─Sequential:3-54[1,512,112,112]--
│ └─Bottleneck:2-7[1,512,112,112]--
│ │ └─Conv2d:3-55[1,128,112,112]65,536
│ │ └─BatchNorm2d:3-56[1,128,112,112]256
│ │ └─Conv2d:3-57[1,128,112,112]147,456
│ │ └─BatchNorm2d:3-58[1,128,112,112]256
│ │ └─Conv2d:3-59[1,512,112,112]65,536
│ │ └─BatchNorm2d:3-60[1,512,112,112]1,024
│ │ └─ChannelAttention:3-61[1,512,1,1]32,768
│ │ └─SpatialAttention:3-62[1,1,1,1]98
│ │ └─Sequential:3-63[1,512,112,112]--
├─Sequential:1-5[1,1024,56,56]--
│ └─Bottleneck:2-8[1,1024,56,56]--
│ │ └─Conv2d:3-64[1,256,112,112]131,072
│ │ └─BatchNorm2d:3-65[1,256,112,112]512
│ │ └─Conv2d:3-66[1,256,56,56]589,824
│ │ └─BatchNorm2d:3-67[1,256,56,56]512
│ │ └─Conv2d:3-68[1,1024,56,56]262,144
│ │ └─BatchNorm2d:3-69[1,1024,56,56]2,048
│ │ └─ChannelAttention:3-70[1,1024,1,1]131,072
│ │ └─SpatialAttention:3-71[1,1,1,1]98
│ │ └─Sequential:3-72[1,1024,56,56]526,336
│ └─Bottleneck:2-9[1,1024,56,56]--
│ │ └─Conv2d:3-73[1,256,56,56]262,144
│ │ └─BatchNorm2d:3-74[1,256,56,56]512
│ │ └─Conv2d:3-75[1,256,56,56]589,824
│ │ └─BatchNorm2d:3-76[1,256,56,56]512
│ │ └─Conv2d:3-77[1,1024,56,56]262,144
│ │ └─BatchNorm2d:3-78[1,1024,56,56]2,048
│ │ └─ChannelAttention:3-79[1,1024,1,1]131,072
│ │ └─SpatialAttention:3-80[1,1,1,1]98
│ │ └─Sequential:3-81[1,1024,56,56]--
│ └─Bottleneck:2-10[1,1024,56,56]--
│ │ └─Conv2d:3-82[1,256,56,56]262,144
│ │ └─BatchNorm2d:3-83[1,256,56,56]512
│ │ └─Conv2d:3-84[1,256,56,56]589,824
│ │ └─BatchNorm2d:3-85[1,256,56,56]512
│ │ └─Conv2d:3-86[1,1024,56,56]262,144
│ │ └─BatchNorm2d:3-87[1,1024,56,56]2,048
│ │ └─ChannelAttention:3-88[1,1024,1,1]131,072
│ │ └─SpatialAttention:3-89[1,1,1,1]98
│ │ └─Sequential:3-90[1,1024,56,56]--
│ └─Bottleneck:2-11[1,1024,56,56]--
│ │ └─Conv2d:3-91[1,256,56,56]262,144
│ │ └─BatchNorm2d:3-92[1,256,56,56]512
│ │ └─Conv2d:3-93[1,256,56,56]589,824
│ │ └─BatchNorm2d:3-94[1,256,56,56]512
│ │ └─Conv2d:3-95[1,1024,56,56]262,144
│ │ └─BatchNorm2d:3-96[1,1024,56,56]2,048
│ │ └─ChannelAttention:3-97[1,1024,1,1]131,072
│ │ └─SpatialAttention:3-98[1,1,1,1]98
│ │ └─Sequential:3-99[1,1024,56,56]--
│ └─Bottleneck:2-12[1,1024,56,56]--
│ │ └─Conv2d:3-100[1,256,56,56]262,144
│ │ └─BatchNorm2d:3-101[1,256,56,56]512
│ │ └─Conv2d:3-102[1,256,56,56]589,824
│ │ └─BatchNorm2d:3-103[1,256,56,56]512
│ │ └─Conv2d:3-104[1,1024,56,56]262,144
│ │ └─BatchNorm2d:3-105[1,1024,56,56]2,048
│ │ └─ChannelAttention:3-106[1,1024,1,1]131,072
│ │ └─SpatialAttention:3-107[1,1,1,1]98
│ │ └─Sequential:3-108[1,1024,56,56]--
│ └─Bottleneck:2-13[1,1024,56,56]--
│ │ └─Conv2d:3-109[1,256,56,56]262,144
│ │ └─BatchNorm2d:3-110[1,256,56,56]512
│ │ └─Conv2d:3-111[1,256,56,56]589,824
│ │ └─BatchNorm2d:3-112[1,256,56,56]512
│ │ └─Conv2d:3-113[1,1024,56,56]262,144
│ │ └─BatchNorm2d:3-114[1,1024,56,56]2,048
│ │ └─ChannelAttention:3-115[1,1024,1,1]131,072
│ │ └─SpatialAttention:3-116[1,1,1,1]98
│ │ └─Sequential:3-117[1,1024,56,56]--
├─Sequential:1-6[1,2048,28,28]--
│ └─Bottleneck:2-14[1,2048,28,28]--
│ │ └─Conv2d:3-118[1,512,56,56]524,288
│ │ └─BatchNorm2d:3-119[1,512,56,56]1,024
│ │ └─Conv2d:3-120[1,512,28,28]2,359,296
│ │ └─BatchNorm2d:3-121[1,512,28,28]1,024
│ │ └─Conv2d:3-122[1,2048,28,28]1,048,576
│ │ └─BatchNorm2d:3-123[1,2048,28,28]4,096
│ │ └─ChannelAttention:3-124[1,2048,1,1]524,288
│ │ └─SpatialAttention:3-125[1,1,1,1]98
│ │ └─Sequential:3-126[1,2048,28,28]2,101,248
│ └─Bottleneck:2-15[1,2048,28,28]--
│ │ └─Conv2d:3-127[1,512,28,28]1,048,576
│ │ └─BatchNorm2d:3-128[1,512,28,28]1,024
│ │ └─Conv2d:3-129[1,512,28,28]2,359,296
│ │ └─BatchNorm2d:3-130[1,512,28,28]1,024
│ │ └─Conv2d:3-131[1,2048,28,28]1,048,576
│ │ └─BatchNorm2d:3-132[1,2048,28,28]4,096
│ │ └─ChannelAttention:3-133[1,2048,1,1]524,288
│ │ └─SpatialAttention:3-134[1,1,1,1]98
│ │ └─Sequential:3-135[1,2048,28,28]--
│ └─Bottleneck:2-16[1,2048,28,28]--
│ │ └─Conv2d:3-136[1,512,28,28]1,048,576
│ │ └─BatchNorm2d:3-137[1,512,28,28]1,024
│ │ └─Conv2d:3-138[1,512,28,28]2,359,296
│ │ └─BatchNorm2d:3-139[1,512,28,28]1,024
│ │ └─Conv2d:3-140[1,2048,28,28]1,048,576
│ │ └─BatchNorm2d:3-141[1,2048,28,28]4,096
│ │ └─ChannelAttention:3-142[1,2048,1,1]524,288
│ │ └─SpatialAttention:3-143[1,1,1,1]98
│ │ └─Sequential:3-144[1,2048,28,28]--
├─AdaptiveAvgPool2d:1-7[1,2048,1,1]--
├─Linear:1-8[1,1000]2,049,000===============================================================================================
Total params:28,065,864
Trainable params:28,065,864
Non-trainable params:0
Total mult-adds (G):63.60===============================================================================================
Input size (MB):0.60
Forward/backward pass size (MB):2691.18
Params size (MB):112.26
Estimated Total Size (MB):2804.04===============================================================================================
版权归原作者 Horizon Max 所有, 如有侵权,请联系我们删除。