主成分分析是一种降维算法，它能将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，其能反映出原始数据的大部分信息
需要了解具体细节可看此视频👉：什么是主成成分分析PCA
计算步骤
假设有
n
n
n 个样本，
p
p
p 个特征，则可构成大小为
n
×
p
n×p
n×p 的样本矩阵
x
x
x
x
=
[
x
11
x
12
…
x
1
p
x
21
x
22
…
x
2
p
⋮
⋮
⋱
⋮
x
n
1
x
n
2
…
x
n
p
]
=
(
x
1
,
x
2
,
…
,
x
p
)
x= \begin{bmatrix} x_{11} & x_{12} & \dots & x_{1p}\\ x_{21} & x_{22} & \dots & x_{2p}\\ \vdots & \vdots & \ddots & \vdots\\ x_{n1} & x_{n2} & \dots & x_{np} \end{bmatrix} =(x_1 , x_2,\ \dots\ , x_p)
x=x11x21⋮xn1x12x22⋮xn2……⋱…x1px2p⋮xnp=(x1,x2, … ,xp)
- 以列为单位，计算各列的均值 x j ‾ \overline{x_j} xj 和标准差 S j S_j Sj ，其中 1 ≤ j ≤ p 1\le j\le p 1≤j≤p x j ‾ = 1 n ∑ i = 1 n x i j S j = ∑ i = 1 n ( x i j − x j ‾ ) 2 n − 1 \overline{x_j}=\dfrac1n\sum_{i=1}^{n}x_{ij}\ S_j=\sqrt{\dfrac{\sum_{i=1}^{n}(x_{ij}-\overline{x_j})^2}{n-1}} xj=n1i=1∑nxijSj=n−1∑i=1n(xij−xj)2
- 标准化原样本矩阵 x x x，标准化样本矩阵为 X X X，标准化后 X i ‾ = 0 \overline{X_i}=0 Xi=0 X i j = x i j − x j ‾ S j [ X 11 X 12 … X 1 p X 21 X 22 … X 2 p ⋮ ⋮ ⋱ ⋮ X n 1 X n 2 … X n p ] X_{ij}=\dfrac{x_{ij}-\overline{x_j}}{S_j}\ \begin{bmatrix} X_{11} & X_{12} & \dots & X_{1p}\ X_{21} & X_{22} & \dots & X_{2p}\ \vdots & \vdots & \ddots & \vdots\ X_{n1} & X_{n2} & \dots & X_{np} \end{bmatrix} Xij=Sjxij−xjX11X21⋮Xn1X12X22⋮Xn2……⋱…X1pX2p⋮Xnp
- 计算标准化样本的协方差矩阵 R R R 【方阵】协方差矩阵求法在线性判别分析LDA中有细致讲解，此处不再赘述 R = [ r 11 r 12 … r 1 p r 21 r 22 … r 2 p ⋮ ⋮ ⋱ ⋮ r p 1 X p 2 … r p p ] r i j = 1 n − 1 ∑ k = 1 n ( X k i − X i ‾ ) ( X k j − X j ‾ ) = 1 n − 1 ∑ k = 1 n X k i X k j R=\begin{bmatrix} r_{11} & r_{12} & \dots & r_{1p}\ r_{21} & r_{22} & \dots & r_{2p}\ \vdots & \vdots & \ddots & \vdots\ r_{p1} & X_{p2} & \dots & r_{pp} \end{bmatrix}\ r_{ij}=\dfrac{1}{n-1}\sum_{k=1}^{n}(X_{ki}-\overline{X_i})(X_{kj}-\overline{X_j}) =\dfrac{1}{n-1}\sum_{k=1}^{n}X_{ki}X_{kj} R=r11r21⋮rp1r12r22⋮Xp2……⋱…r1pr2p⋮rpprij=n−11k=1∑n(Xki−Xi)(Xkj−Xj)=n−11k=1∑nXkiXkj
- 计算 R R R 的特征值和特征矩阵【参考考研数学线性代数部分】 R R R 是半正定矩阵，特征值 λ \lambda λ 有如下👇性质 λ 1 ≥ λ 2 ≥ ⋯ ≥ 0 t r ( R ) = ∑ k = 1 p λ k = p \lambda_1\ge\lambda_2\ge\dots\ge0\ tr(R)=\sum_{k=1}^{p}\lambda_k=p λ1≥λ2≥⋯≥0tr(R)=k=1∑pλk=p
- 计算主成分贡献率 r a t e _ o f _ c o n t r i b u t i o n rate_of_contribution rate_of_contribution 以及累计贡献率 a g g r e g a t e _ r a t e _ o f _ c o n t r i b u t i o n aggregate_rate_of_contribution aggregate_rate_of_contribution r a t e _ o f _ c o n t r i b u t i o n = λ i ∑ k = 1 p λ k ( i = 1 , 2 , … , p ) a g g r e g a t e _ r a t e _ o f _ c o n t r i b u t i o n = ∑ k = 1 i λ k ∑ k = 1 p λ k ( i = 1 , 2 , … , p ) rate_of_contribution=\dfrac{\lambda_i}{\sum_{k=1}^{p}\lambda_k}(i=1,2,\ \dots\ ,p)\ aggregate_rate_of_contribution=\dfrac{\sum_{k=1}^{i}\lambda_k}{\sum_{k=1}^{p}\lambda_k}(i=1,2,\ \dots\ ,p) rate_of_contribution=∑k=1pλkλi(i=1,2, … ,p)aggregate_rate_of_contribution=∑k=1pλk∑k=1iλk(i=1,2, … ,p)
- 写出主成分，第 i i i 个主成分记作 y i y_i yi一般取累计贡献率超过 80 % 80% 80% 的特征值所对应的第一、第二、 … \dots … 、第 m ( m ≤ p ) m(m\le p) m(m≤p) 个主成分 y i = a 1 i X 1 + a 2 i X 2 + ⋯ + a p i X p ( i = 1 , 2 , … , m ) y_i=a_{1i}X_1+a_{2i}X_2+\dots+a_{pi}X_p \ \ \ \ \ (i=1,2,\ \dots\ ,m) yi=a1iX1+a2iX2+⋯+apiXp (i=1,2, … ,m) 其中 a a a 是特征向量【竖直】， a 1 i a_{1i} a1i 代表第 i i i 个特征向量的第 1 1 1 个元素
- 根据系数分析主成分代表的意义> 对于某个主成分而言，指标前面的系数越大，代表该指标对于该主成分的影响越大
例题
假设有
n
n
n 个学生参加四门课程的考试，将学生们的考试成绩看作随机变量的取值，对考试成绩数据进行标准化处理，得到样本相关矩阵
R
R
R ，如下表所示👇：
试对数据进行主成分分析。
此处的矩阵已经是协方差矩阵，因此直接计算特征值和特征向量即可
import numpy as np
R = np.array([[1,0.44,0.29,0.33],[0.44,1,0.35,0.32],[0.29,0.35,1,0.6],[0.33,0.32,0.6,1]])
eigenvalue, featurevector = np.linalg.eig(a)print('特征值：')print(eigenvalue)print('特征向量：')# numpy计算的特征向量最后需要变号print(featurevector*(-1))
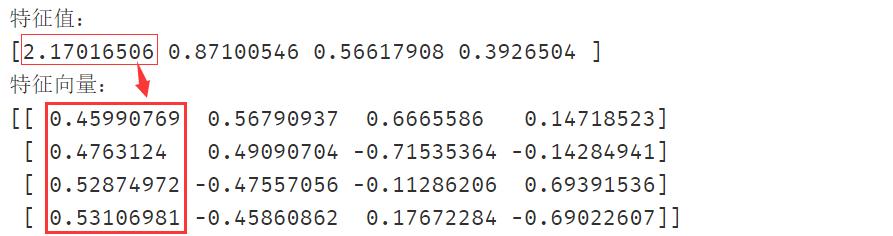
特征值和特征向量值可能会有误差，这是因为计算时位数的不同，总体差不多即可，此处做近似处理使得结果与例题一致
∴
λ
1
=
2.17
,
λ
2
=
0.87
,
λ
3
=
0.57.
λ
4
=
0.39
\therefore \lambda_1=2.17,\ \lambda_2=0.87,\ \lambda_3=0.57.\ \lambda_4=0.39
∴λ1=2.17, λ2=0.87, λ3=0.57. λ4=0.39
这些特征值就是各主成分的方差贡献值。假设要求主成分的累计方差贡献率大于
75
%
75\%
75% 那么只需取前两个主成分即可，即
k
=
2
k=2
k=2 ，因为👇
a
g
g
r
e
g
a
t
e
_
r
a
t
e
_
o
f
_
c
o
n
t
r
i
b
u
t
i
o
n
=
∑
k
=
1
2
λ
k
∑
k
=
1
4
λ
k
=
2.17
+
0.87
2.17
+
0.87
+
0.57
+
0.39
=
0.76
aggregate\_rate\_of\_contribution=\dfrac{\sum_{k=1}^{2}\lambda_k}{\sum_{k=1}^{4}\lambda_k}=\dfrac{2.17+0.87}{2.17+0.87+0.57+0.39}=0.76
aggregate_rate_of_contribution=∑k=14λk∑k=12λk=2.17+0.87+0.57+0.392.17+0.87=0.76
近似处理单位特征向量和主成分的方差贡献率
项目
x
1
x_1
x1
x
2
x_2
x2
x
3
x_3
x3
x
4
x_4
x4方差贡献率【
r
a
t
e
_
o
f
_
c
o
n
t
r
i
b
u
t
i
o
n
rate\_of\_contribution
rate_of_contribution】
y
1
y_1
y10.4600.4760.5230.5370.543
y
2
y_2
y20.5740.486-0.476-0.4560.218
第一，第二主成分为：
y
1
=
0.460
x
1
+
0.476
x
2
+
0.523
x
3
+
0.537
x
4
y
1
=
0.574
x
1
+
0.486
x
2
−
0.476
x
3
−
0.456
x
4
y_1=0.460x_1+0.476x_2+0.523x_3+0.537x_4\\ y_1=0.574x_1+0.486x_2-0.476x_3-0.456x_4
y1=0.460x1+0.476x2+0.523x3+0.537x4y1=0.574x1+0.486x2−0.476x3−0.456x4
第
i
i
i 主成分对应变量
x
j
x_j
xj 的因子负荷量
f
i
j
f_{ij}
fij =
a
i
j
×
λ
i
σ
i
j
\dfrac{a_{ij} \times\sqrt{\lambda_i}}{\sqrt{\sigma_{ij}}}
σijaij×λi ，其中
a
i
j
a_{ij}
aij 是第
i
i
i 个特征向量的第
j
j
j 个元素，
σ
i
j
\sigma_{ij}
σij 是协方差
r
i
j
r_{ij}
rij
f
11
=
0.460
×
2.17
1
=
0.678
f_{11}= \dfrac{0.460 \times \sqrt{2.17}}{\sqrt{1}}=0.678
f11=10.460×2.17=0.678
同理可得其余的因子负荷量
第 i 主成分对应变量xj的因子负荷量
项目
x
1
x_1
x1
x
2
x_2
x2
x
3
x_3
x3
x
4
x_4
x4
y
1
y_1
y10.6780.7010.7700.791
y
2
y_2
y20.5360.453-0.444-0.425
第
x
,
y
x,y
x,y 主成分对变量
x
i
x_i
xi 的贡献率
p
x
y
,
i
=
f
x
i
2
+
f
y
i
2
p_{xy,i}= f_{xi}^2+ {f_{yi}^2}
pxy,i=fxi2+fyi2 ，其中
f
i
j
f_{ij}
fij 为第
i
i
i 主成分对应第
j
j
j 个因子负荷量
p
12
,
1
=
0.67
8
2
+
0.53
6
2
=
0.747
p_{12,1}=0.678^2+0.536^2=0.747
p12,1=0.6782+0.5362=0.747
同理可得其余的贡献率
第 1，2 主成分对变量 xi 的贡献率
x
1
x_1
x1
x
2
x_2
x2
x
3
x_3
x3
x
4
x_4
x40.7470.6970.7900.806
可以看出，第一主成分
y
1
y_1
y1 对应的因子负荷量均为正数，表明各门课程成绩提高都可使
y
1
y_1
y1 提高，也就是说，第一主成分
y
1
y_1
y1 反映了学生的整体成绩；还可以看出，因子负荷量的数值相近，且
y
1
(
x
4
)
y_1(x_4)
y1(x4) 的数值最大，这表明物理成绩在整体成绩中占最重要位置。
第二主成分
y
2
y_2
y2 对应的因子负荷量有正有负，正的是语文和外语，负的是数学和物理，表明文科成绩提高都可使
y
2
y_2
y2 提高，而理科成绩提高都可使
y
2
y_2
y2 降低，也就是说，第二主成分
y
2
y_2
y2 反映了学生的文科成绩与理科成绩的关系。
本文转载自: https://blog.csdn.net/weixin_45488428/article/details/130540349
版权归原作者 Infinity_and_beyond 所有， 如有侵权，请联系我们删除。
版权归原作者 Infinity_and_beyond 所有， 如有侵权，请联系我们删除。