论文下载地址:https://arxiv.org/abs/2101.03697
官方源码(Pytorch实现):GitHub - DingXiaoH/RepVGG: RepVGG: Making VGG-style ConvNets Great Again
写这边博客也是为了做一个记录,如果有错误或者不足,请各位大佬提出。
repvgg参考了博主:太阳花小绿豆的博客地址如下:
(19条消息) RepVGG网络简介_太阳花的小绿豆的博客-CSDN博客
在开始前简单说一下我的理解repvgg到底再做什么,我用简单的话来说就是设计了一个可融合的网络,在模型的推理的时候将含有多分支的模型转化为单分支的结构,加快推理的速度。
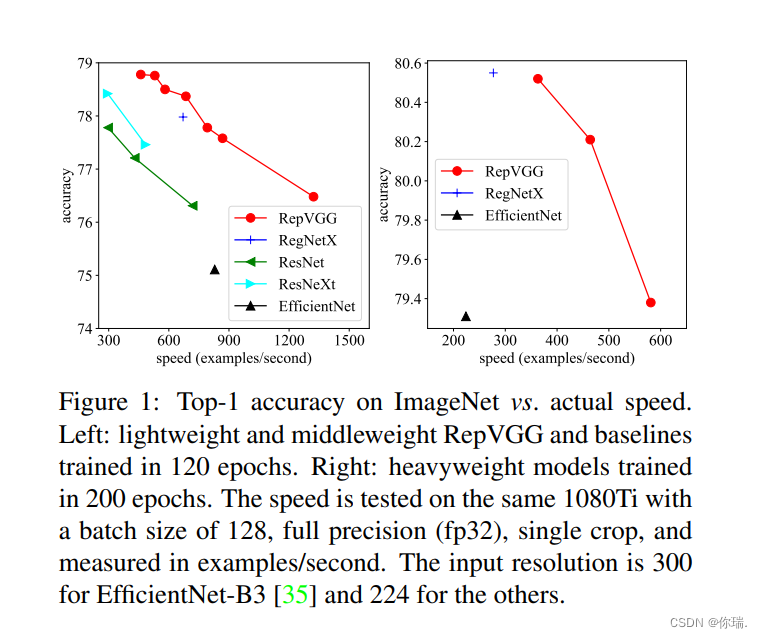
再论文中作者给出了一个对比,repvgg的网络再imagenet上表现不错,而且在相同准确率下推理速度已经接近Efficientnet的三倍,这就得益于它的多分支融合的技术,听上去高大上其实还是很简单的。
废话不多说直接上图:
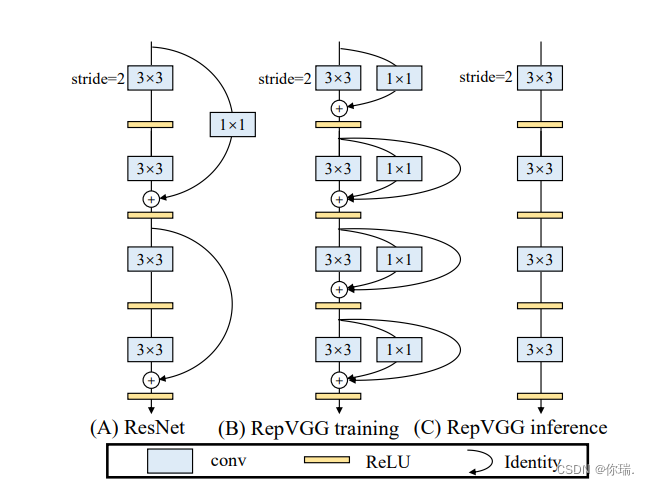
原论文中的结构图很直观的展示了repvgg到底是什么意思,对比Resnet它仍然有着类似残差的结构,就是在33的卷积基础上弄了一个11的分支和一个identity分支(在步长不等于2且输入输出通道相等的情况下),这样除了方便推理过程的融合,似乎还有多分支的好处,因为有丰富的梯度信息(狗头保命),但是这好像会在训练时增加参数量,但是推理速度快就ok了。
具体融合的过程结合论文中给出来的图去讲解:
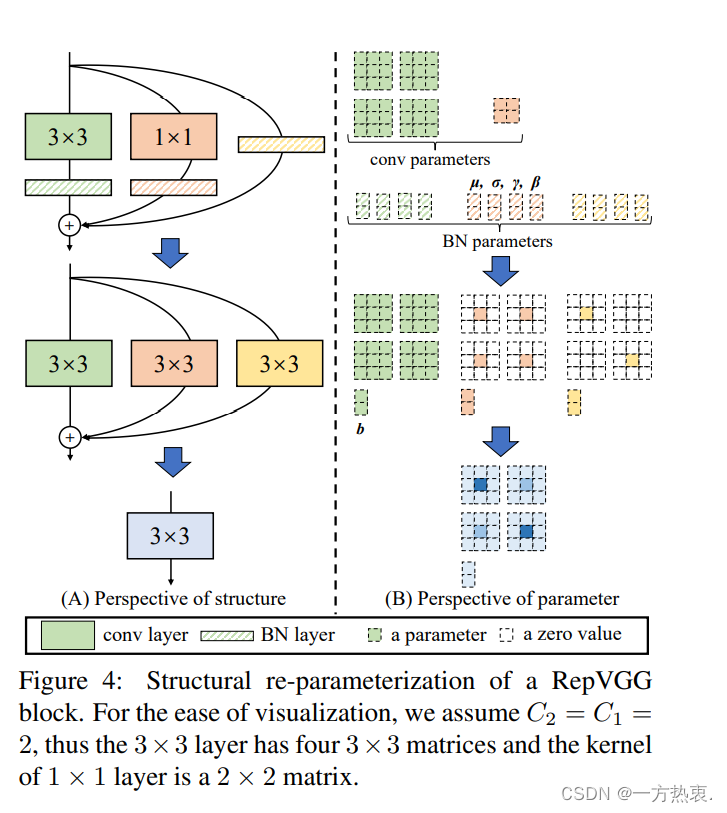
假设你的输出和输入通道都是2,那么对于33的卷积就有两个通道为2的33的卷积核,11也一样,就像图中四个绿色的方框和四个橙色的方框,对于BN层来说,里面有,这几个参数具体来说就是均值,方差,权重,偏置,他们也和通道的输入维度保持一致,融合的步骤就是卷积操作和BN层分别进行融合,主要需要改变的还是11的卷积如何变成33的卷积,identity分支怎么转换成33的模样。到这里可能会有质疑这种融合后能和以前一样吗,那么我们从公式入手:
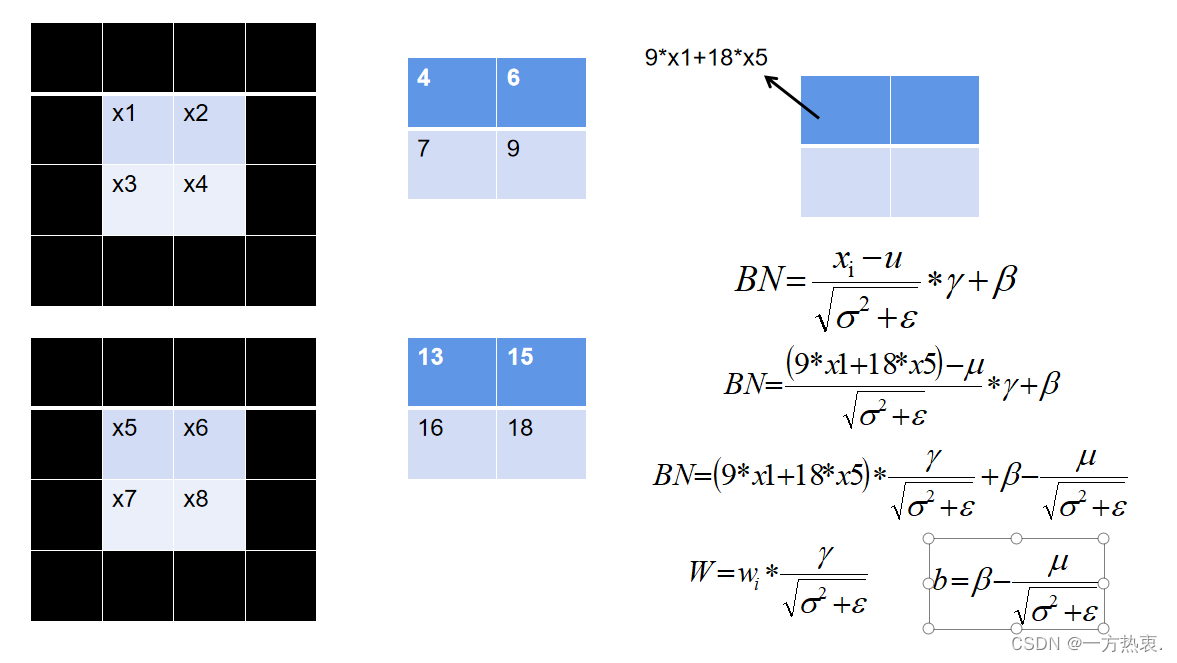
图中我们以2*2卷积为例,为了保持输入与输出同尺寸,黑色的一圈为padding,我们只计算出第一个特征点的值对于第一个特征点,我们将值带入BN的计算公式:
这里是一个极小的数防止分母为0将BN公式转变一下就变成:
那么我们如果不要融合conv和bn是不是就可以把参数项直接乘到卷积核的权重里去,我们普通卷积是没有偏执的,然后剩下的作为偏执加载到融合后的conv中:
这样我们就将conv与bn融合,接下来让我们看看代码中是怎么完成的:
def _fuse_bn_tensor(self, branch):
if branch is None:
return 0, 0
if isinstance(branch, nn.Sequential):
kernel = branch[0].weight
running_mean = branch[1].running_mean
running_var = branch[1].running_var
gamma = branch[1].weight
beta = branch[1].bias
eps = branch[1].eps
else:
assert isinstance(branch, nn.BatchNorm2d)
if not hasattr(self, "id_tensor"):
input_dim = self.in_channels // self.groups
kernel_value = np.zeros(
(self.in_channels, input_dim, 3, 3), dtype=np.float32
)
for i in range(self.in_channels):
kernel_value[i, i % input_dim, 1, 1] = 1
self.id_tensor = torch.from_numpy(kernel_value).to(branch.weight.device)
kernel = self.id_tensor
running_mean = branch.running_mean
running_var = branch.running_var
gamma = branch.weight
beta = branch.bias
eps = branch.eps
std = (running_var + eps).sqrt()
t = (gamma / std).reshape(-1, 1, 1, 1)
return kernel * t, beta - running_mean * gamma / std
这里函数接收的是一个nn.Sequential(),里面是一个卷积操作以及一个bn层,我们依次取出卷积的weight,以及bn层的各个参数,然后在下面放回计算后的weight,bias,这里代码中else是当传入的是identity分支时,也就是只有BN层的时候,我们要构造出一个33的卷积,这里不像11的卷积我们只需要padding一圈0就可以了,identity分支需要特殊的构造方式,要求卷积操作后,输入不变,文中作者是这样做的:
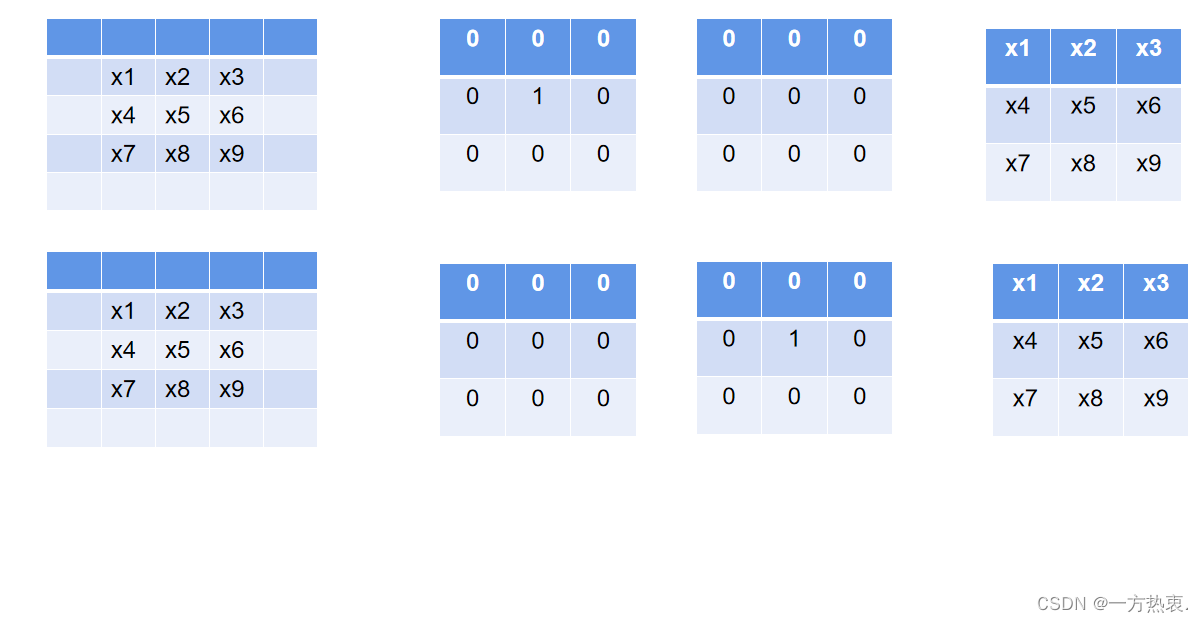
设计卷积核只有中间为1,其余一圈0,这样卷积完成后和输入特征值没有发生变化,在代码中是这样实时的:
else:
assert isinstance(branch, nn.BatchNorm2d)
if not hasattr(self, "id_tensor"):
input_dim = self.in_channels // self.groups
kernel_value = np.zeros(
(self.in_channels, input_dim, 3, 3), dtype=np.float32
)
for i in range(self.in_channels):
kernel_value[i, i % input_dim, 1, 1] = 1
self.id_tensor = torch.from_numpy(kernel_value).to(branch.weight.device)
先构造一个全为0的卷积核然后在相应位置复值1.
我们依次将三个分支卷积层和BN层的参数全部取出来然后相加:
def get_equivalent_kernel_bias(self):
kernel3x3, bias3x3 = self._fuse_bn_tensor(self.rbr_dense)
kernel1x1, bias1x1 = self._fuse_bn_tensor(self.rbr_1x1)
kernelid, biasid = self._fuse_bn_tensor(self.rbr_identity)
return (
kernel3x3 + self._pad_1x1_to_3x3_tensor(kernel1x1) + kernelid,
bias3x3 + bias1x1 + biasid,
)
这样我们就获得了融合后的33卷积的bias和weight,最后先创建一个33卷积但是bias要设置为Ture,然后我们将准备好的weight和bias加载到这个3*3卷积层中:
def fuse_conv_bn(self, conv, bn):
kernel, bias = self.get_equivalent_kernel_bias()
conv = nn.Conv2d(in_channels = conv.in_channels,
out_channels = conv.out_channels,
kernel_size = conv.kernel_size,
stride=conv.stride,
padding = conv.padding,
dilation = conv.dilation,
groups = conv.groups,
bias = True,
padding_mode = conv.padding_mode)
conv.weight = torch.nn.Parameter(kernel)
conv.bias = torch.nn.Parameter(bias)
return conv
这样我们就将三个分支融合成了一个分支,这样的在推理的时候就会非常快,而且很省内存
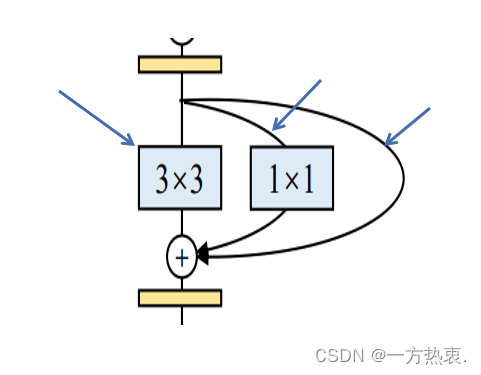
更快的话主要就是像这种最后要有一个add操作,11和这个identity分支肯定是率先完成的,但是就算它完成了也要等33卷积操作结束后才能释放当前算力,如果融合后就只需要通过一个3*3卷积就可以了,还有一种解释是每当此启动kernel都是需要消耗时间的,相比之下一条路直接下来显然更快。
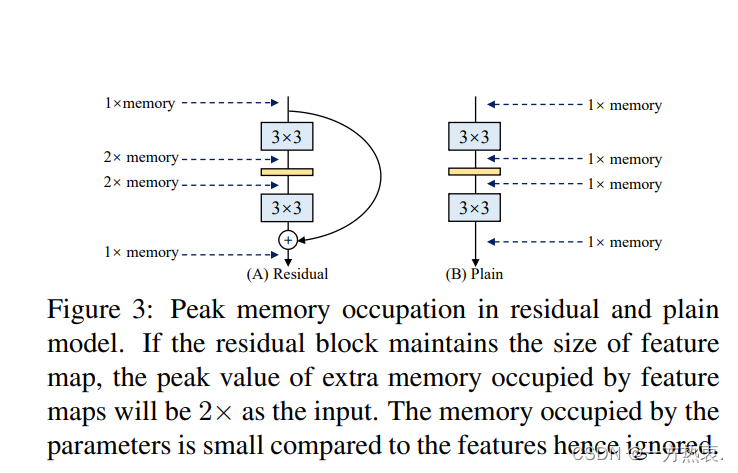
原文中的意思是像这残差分支,会一直占用1x的内存,直到add操作后才会释放,所以repvgg提出的参数重构化就很好的解决了推理时的内存占用和推理速度等方面。目前repvgg的结构已经被应用与很多任务中,就拿今年的目标检测任务中,从PP-YOLOE,到yolov6和yolov7都应用这种结构,让部署更容易,检测效果间接提升,相信在以后的任务中repvgg依然可以发光。
版权归原作者 一方热衷. 所有, 如有侵权,请联系我们删除。