本节主要介绍另外两个基本信号，在连续时间和离散时间情况下的单位阶跃和单位冲激函数，在信号与系统的分析中很重要。
单位阶跃函数
值得注意的是单位阶跃在t=0这一点是不连续的。
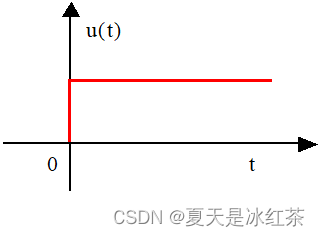
单位冲激函数
狄拉克定义：
以及
同理：
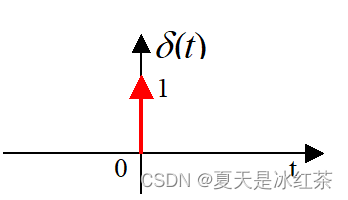
冲激函数的性质
对时间的积分等于单位阶跃函数
连续时间单位冲激可看作连续时间单位阶跃的一次微分
筛分性质
以及
可以看看下面的三个例题：
尺度特性
冲击偶的定义：单位冲击函数的导数
各阶导数
离散的阶跃信号与冲激信号
（1）阶跃信号，其定义为：
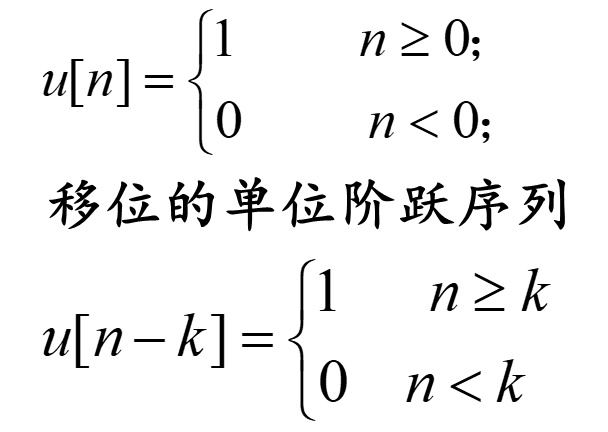
（2）冲激信号，其定义为：
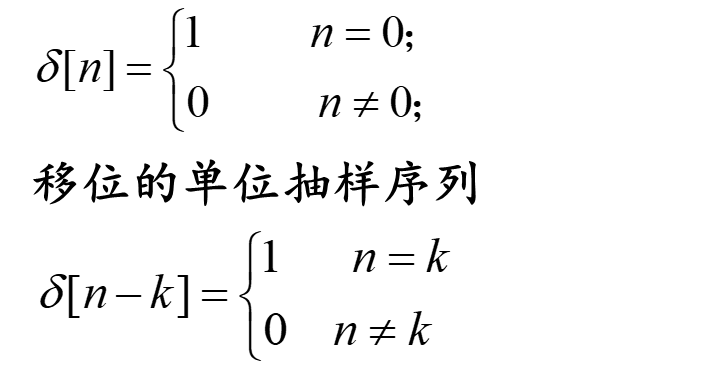
**冲激信号与阶跃信号的关系为： **
离散时间单位脉冲是离散时间单位阶跃的一次差分，相反，离散时间阶跃是单位样本的求和函数。
筛分性质：
本文转载自: https://blog.csdn.net/m0_62919535/article/details/129310523
版权归原作者 夏天是冰红茶 所有， 如有侵权，请联系我们删除。
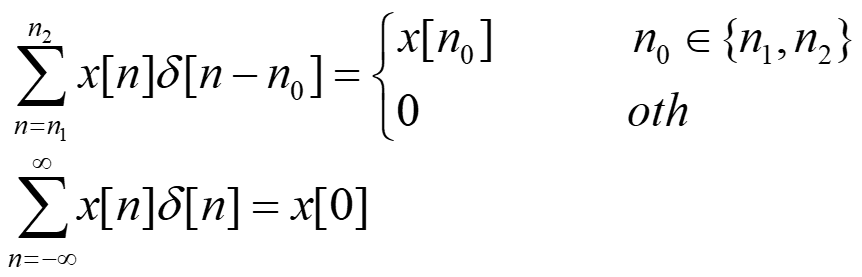
版权归原作者 夏天是冰红茶 所有， 如有侵权，请联系我们删除。