自然语言处理2-NLP
在自然语言处理任务中,词向量(Word Embedding)是表示自然语言里单词的一种方法,即把每个词都表示为一个N维空间内的点,即一个高维空间内的向量。通过这种方法,实现把自然语言计算转换为向量计算。
如 图1 所示的词向量计算任务中,先把每个词(如queen,king等)转换成一个高维空间的向量,这些向量在一定意义上可以代表这个词的语义信息。再通过计算这些向量之间的距离,就可以计算出词语之间的关联关系,从而达到让计算机像计算数值一样去计算自然语言的目的。

图1:词向量计算示意图
因此,大部分词向量模型都需要回答两个问题:
- 如何把词转换为向量?
自然语言单词是离散信号,比如“香蕉”,“橘子”,“水果”在我们看来就是3个离散的词。
如何把每个离散的单词转换为一个向量?
- 如何让向量具有语义信息?
比如,我们知道在很多情况下,“香蕉”和“橘子”更加相似,而“香蕉”和“句子”就没有那么相似,同时“香蕉”和“食物”、“水果”的相似程度可能介于“橘子”和“句子”之间。
那么,我们该如何让词向量具备这样的语义信息?
如何把词转换为向量
自然语言单词是离散信号,比如“我”、“ 爱”、“人工智能”。如何把每个离散的单词转换为一个向量?通常情况下,我们可以维护一个如 图2 所示的查询表。表中每一行都存储了一个特定词语的向量值,每一列的第一个元素都代表着这个词本身,以便于我们进行词和向量的映射(如“我”对应的向量值为 [0.3,0.5,0.7,0.9,-0.2,0.03] )。给定任何一个或者一组单词,我们都可以通过查询这个excel,实现把单词转换为向量的目的,这个查询和替换过程称之为Embedding Lookup。

图2:词向量查询表
上述过程也可以使用一个字典数据结构实现。事实上如果不考虑计算效率,使用字典实现上述功能是个不错的选择。然而在进行神经网络计算的过程中,需要大量的算力,常常要借助特定硬件(如GPU)满足训练速度的需求。GPU上所支持的计算都是以张量(Tensor)为单位展开的,因此在实际场景中,我们需要把Embedding Lookup的过程转换为张量计算,如 图3 所示。
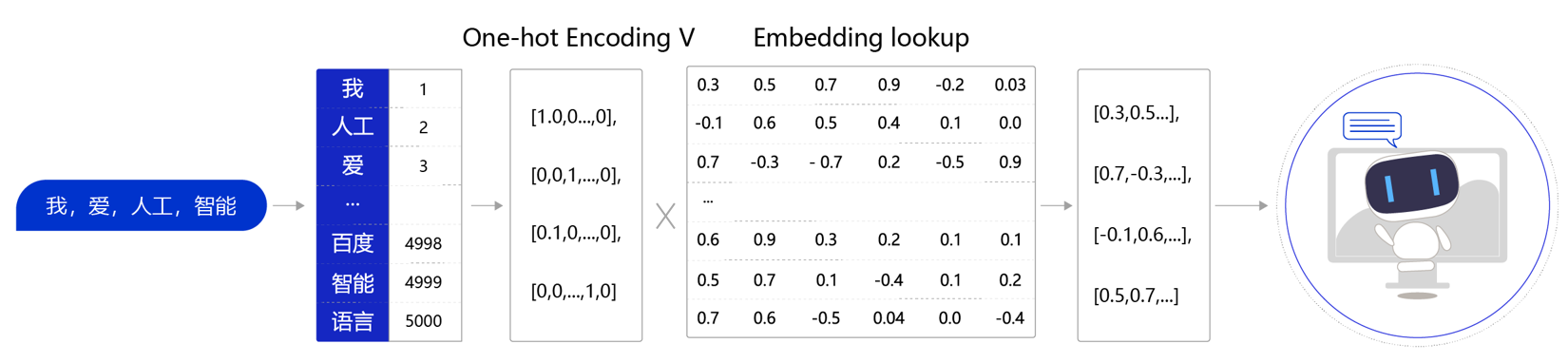
图3:张量计算示意图
假设对于句子"我,爱,人工,智能",把Embedding Lookup的过程转换为张量计算的流程如下:
- 通过查询字典,先把句子中的单词转换成一个ID(通常是一个大于等于0的整数),这个单词到ID的映射关系可以根据需求自定义(如图3中,我=>1, 人工=>2,爱=>3,…)。
- 得到ID后,再把每个ID转换成一个固定长度的向量。假设字典的词表中有5000个词,那么,对于单词“我”,就可以用一个5000维的向量来表示。由于“我”的ID是1,因此这个向量的第一个元素是1,其他元素都是0([1,0,0,…,0]);
- 同样对于单词“人工”,第二个元素是1,其他元素都是0。
- 用这种方式就实现了用一个向量表示一个单词。由于每个单词的向量表示都只有一个元素为1,而其他元素为0,因此我们称上述过程为One-Hot Encoding。
- 经过One-Hot Encoding后,句子“我,爱,人工,智能”就被转换成为了一个形状为 4×5000的张量,记为V。在这个张量里共有4行、5000列,从上到下,每一行分别代表了“我”、“爱”、“人工”、“智能”四个单词的One-Hot Encoding。最后,我们把这个张量V和另外一个稠密张量W相乘,其中W张量的形状为5000 × 128(5000表示词表大小,128表示每个词的向量大小)。经过张量乘法,我们就得到了一个4×128的张量,从而完成了把单词表示成向量的目的。
如何让向量具有语义信息
得到每个单词的向量表示后,我们需要思考下一个问题:比如在多数情况下,“香蕉”和“橘子”更加相似,而“香蕉”和“句子”就没有那么相似;同时,“香蕉”和“食物”、“水果”的相似程度可能介于“橘子”和“句子”之间。那么如何让存储的词向量具备这样的语义信息呢?
我们先学习自然语言处理领域的一个小技巧。在自然语言处理研究中,科研人员通常有一个共识:使用一个单词的上下文来了解这个单词的语义,比如:
“苹果手机质量不错,就是价格有点贵。”
“这个苹果很好吃,非常脆。”
“菠萝质量也还行,但是不如苹果支持的APP多。”
在上面的句子中,我们通过上下文可以推断出第一个“苹果”指的是苹果手机,第二个“苹果”指的是水果苹果,而第三个“菠萝”指的应该也是一个手机。事实上,
在自然语言处理领域,使用上下文描述一个词语或者元素的语义是一个常见且有效的做法。
我们可以使用同样的方式训练词向量,让这些词向量具备表示语义信息的能力。
2013年,Mikolov提出的经典word2vec算法就是通过上下文来学习语义信息。word2vec包含两个经典模型:CBOW(Continuous Bag-of-Words)和Skip-gram,如 图4 所示。
- CBOW:通过上下文的词向量推理中心词。
- Skip-gram:根据中心词推理上下文。
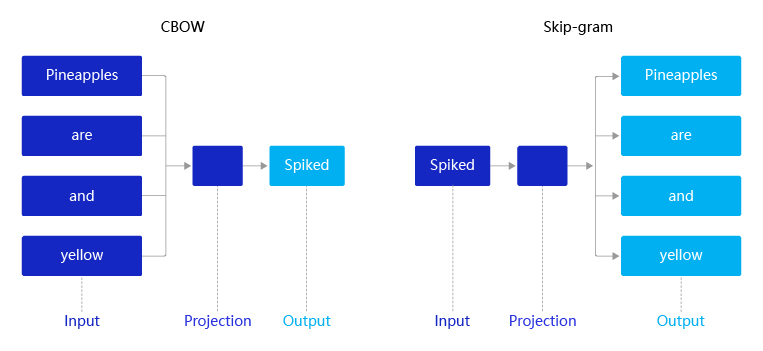
图4:CBOW和Skip-gram语义学习示意图
假设有一个句子“Pineapples are spiked and yellow”,两个模型的推理方式如下:
在CBOW中
- 先在句子中选定一个中心词,并把其它词作为这个中心词的上下文。如 图4 CBOW所示,把“Spiked”作为中心词,把“Pineapples、are、and、yellow”作为中心词的上下文。在学习过程中,使用上下文的词向量推理中心词,这样中心词的语义就被传递到上下文的词向量中,如“Spiked → pineapple”,从而达到学习语义信息的目的。
在Skip-gram中
- 同样先选定一个中心词,并把其他词作为这个中心词的上下文。如 图4 Skip-gram所示,把“Spiked”作为中心词,把“Pineapples、are、and、yellow”作为中心词的上下文。不同的是,在学习过程中,使用中心词的词向量去推理上下文,这样上下文定义的语义被传入中心词的表示中,如“pineapple → Spiked”, 从而达到学习语义信息的目的。
说明:
一般来说,CBOW比Skip-gram训练速度快,训练过程更加稳定,原因是CBOW使用上下文average的方式进行训练,每个训练step会见到更多样本。
而在生僻字(出现频率低的字)
skip-gram比CBOW效果更好
原因是skip-gram不会刻意回避生僻字(CBOW结构中输入中存在生僻字时,生僻字会被其它非生僻字的权重冲淡)。
CBOW和Skip-gram的算法实现
我们以这句话:“Pineapples are spiked and yellow”为例分别介绍CBOW和Skip-gram的算法实现。
如 图5 所示,CBOW是一个具有3层结构的神经网络,分别是:

图5:CBOW的算法实现
- 输入层: 一个形状为C×V的one-hot张量,其中C代表上线文中词的个数,通常是一个偶数,我们假设为4;V表示词表大小,我们假设为5000,该张量的每一行都是一个上下文词的one-hot向量表示,比如“Pineapples, are, and, yellow”。
- 隐藏层: 一个形状为V×N的参数张量W1,一般称为word-embedding,N表示每个词的词向量长度,我们假设为128。输入张量和word embedding W1进行矩阵乘法,就会得到一个形状为C×N的张量。综合考虑上下文中所有词的信息去推理中心词,因此将上下文中C个词相加得一个1×N的向量,是整个上下文的一个隐含表示。
- 输出层: 创建另一个形状为N×V的参数张量,将隐藏层得到的1×N的向量乘以该N×V的参数张量,得到了一个形状为1×V的向量。最终,1×V的向量代表了使用上下文去推理中心词,每个候选词的打分,再经过softmax函数的归一化,即得到了对中心词的推理概率:
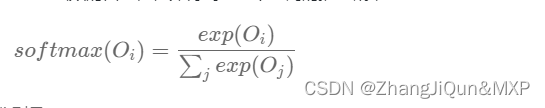
如 图6 所示,Skip-gram是一个具有3层结构的神经网络,分别是:
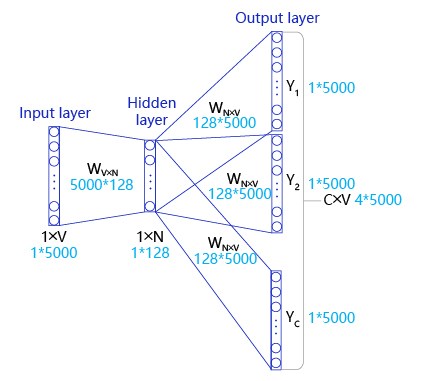
图6:Skip-gram算法实现

在实际操作中,使用一个滑动窗口(一般情况下,长度是奇数),从左到右开始扫描当前句子。每个扫描出来的片段被当成一个小句子,每个小句子中间的词被认为是中心词,其余的词被认为是这个中心词的上下文。
Skip-gram的理想实现

Skip-gram的实际实现


版权归原作者 ZhangJiQun&MXP 所有, 如有侵权,请联系我们删除。