三种Transformer模型中的注意力机制介绍及Pytorch实现：从自注意力到因果自注意力

本文深入探讨Transformer模型中三种关键的注意力机制：自注意力、交叉注意力和因果自注意力。这些机制是GPT-4、Llama等大型语言模型（LLMs）的核心组件。通过理解这些注意力机制，我们可以更好地把握这些模型的工作原理和应用潜力。

我们不仅会讨论理论概念，还将使用Python和PyTorch从零开始实现这些注意力机制。通过实际编码，我们可以更深入地理解这些机制的内部工作原理。

文章目录

1. 自注意力机制- 理论基础- PyTorch实现- 多头注意力扩展
2. 交叉注意力机制- 概念介绍- 与自注意力的区别- PyTorch实现
3. 因果自注意力机制- 在语言模型中的应用- 实现细节- 优化技巧

通过这种结构，我们将逐步深入每种注意力机制从理论到实践提供全面的理解。让我们首先从自注意力机制开始，这是Transformer架构的基础组件。

自注意力概述

自注意力机制自2017年在开创性论文《Attention Is All You Need》中被提出以来，已成为最先进深度学习模型的核心，尤其是在自然语言处理（NLP）领域。考虑到其广泛应用，深入理解自注意力的运作机制变得尤为重要。

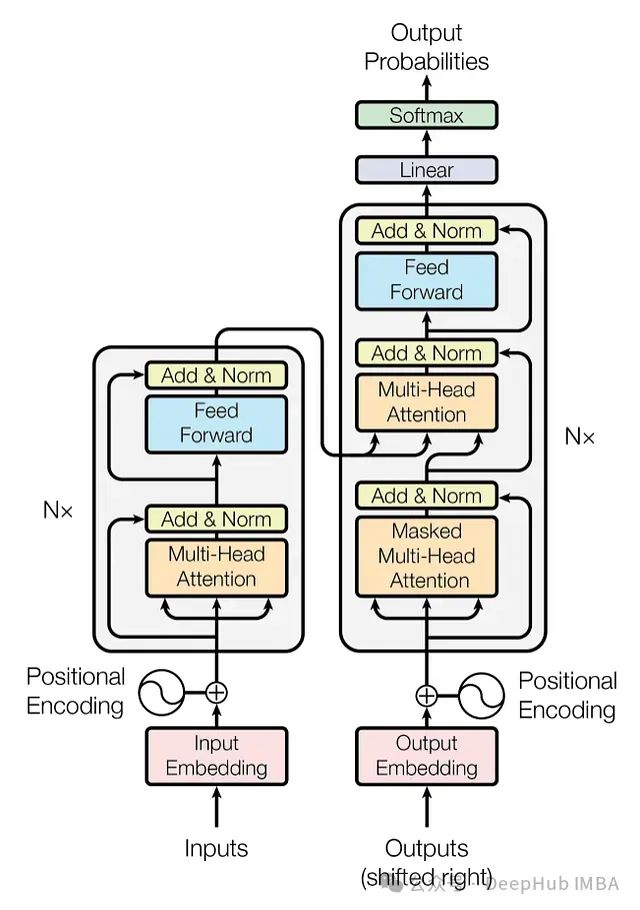
图1：原始Transformer架构

在深度学习中，"注意力"概念的引入最初是为了改进递归神经网络（RNNs）处理长序列或句子的能力。例如，在机器翻译任务中，逐字翻译通常无法捕捉语言的复杂语法和表达方式，导致翻译质量低下。

为解决这一问题，注意力机制使模型能够在每个步骤考虑整个输入序列，有选择地关注上下文中最相关的部分。2017年引入的Transformer架构进一步发展了这一概念，将自注意力作为独立机制整合，使得RNNs不再必要。

图2：注意力机制可视化

自注意力允许模型通过整合上下文信息来增强输入嵌入，使其能够动态地权衡序列中不同元素的重要性。这一特性在NLP中尤其有价值，因为词语的含义往往随其在句子或文档中的上下文而变化。

尽管已提出多种高效版本的自注意力，但《Attention Is All You Need》中引入的原始缩放点积注意力机制仍然是应用最广泛的。由于其在大规模Transformer模型中表现出色的实际性能和计算效率，它仍然是许多模型的基础。

输入句子嵌入

在深入探讨自注意力机制之前，我们先通过一个示例句子"The sun rises in the east"来演示操作过程。与其他文本处理模型（如递归或卷积神经网络）类似，第一步是创建句子嵌入。

为简化说明，我们的字典

dc

仅包含输入句子中的单词。在实际应用中，字典通常从更大的词汇表构建，一般包含30,000到50,000个单词。

 sentence='The sun rises in the east'  
 
 dc= {s:ifori,sinenumerate(sorted(sentence.split()))}  
 
 print(dc)

输出：

 {'The': 0, 'east': 1, 'in': 2, 'rises': 3, 'sun': 4, 'the': 5}

接下来，我们使用这个字典将句子中的每个单词转换为其对应的整数索引。

 importtorch  
 
 sentence_int=torch.tensor(  
     [dc[s] forsinsentence.split()]  
 )  
 print(sentence_int)

输出：

 tensor([0, 4, 3, 2, 5, 1])

有了这个输入句子的整数表示，可以使用嵌入层将每个单词转换为向量。为简化演示，我们这里使用3维嵌入，但在实际应用中，嵌入维度通常要大得多（例如，Llama 2模型中使用4,096维）。较小的维度有助于直观理解向量而不会使页面充满数字。

由于句子包含6个单词，嵌入将生成一个6×3维矩阵。

 vocab_size=50_000  
 
 torch.manual_seed(123)  
 embed=torch.nn.Embedding(vocab_size, 3)  
 embedded_sentence=embed(sentence_int).detach()  
 
 print(embedded_sentence)  
 print(embedded_sentence.shape)

输出：

 tensor([[ 0.3374, -0.1778, -0.3035],  
         [ 0.1794,  1.8951,  0.4954],  
         [ 0.2692, -0.0770, -1.0205],  
         [-0.2196, -0.3792,  0.7671],  
         [-0.5880,  0.3486,  0.6603],  
         [-1.1925,  0.6984, -1.4097]])  
 torch.Size([6, 3])

这个6×3矩阵表示输入句子的嵌入版本，每个单词被编码为一个3维向量。虽然实际模型中的嵌入维度通常更高，但这个简化示例有助于我们理解嵌入的工作原理。

缩放点积注意力的权重矩阵

完成输入嵌入后，首先探讨自注意力机制，特别是广泛使用的缩放点积注意力，这是Transformer模型的核心元素。

缩放点积注意力机制使用三个权重矩阵：Wq、Wk和Wv。这些矩阵在模型训练过程中优化，用于转换输入数据。

查询、键和值的转换

权重矩阵将输入数据投影到三个组成部分：

1. 查询 (q)
2. 键 (k)
3. 值 (v)

这些组成部分通过矩阵乘法计算得出：

• 查询：q(i) = x(i)Wq
• 键：k(i) = x(i)Wk
• 值：v(i) = x(i)Wv

这里，'i'表示输入序列中长度为T的token位置。

图3：通过输入x和权重W计算查询、键和值向量

这个操作实际上是将每个输入token x(i)投影到这三个不同的空间中。

关于维度，q(i)和k(i)都是具有dk个元素的向量。投影矩阵Wq和Wk的形状为d × dk，而Wv为d × dv。这里，d是每个词向量x的大小。

需要注意的是q(i)和k(i)必须具有相同数量的元素（dq = dk），因为后续会计算它们的点积。许多大型语言模型为简化设置dq = dk = dv，但v(i)的大小可以根据需要不同。

以下是一个代码示例：

 torch.manual_seed(123)  
 
 d=embedded_sentence.shape[1]  
 
 d_q, d_k, d_v=2, 2, 4  
 
 W_query=torch.nn.Parameter(torch.rand(d, d_q))  
 W_key=torch.nn.Parameter(torch.rand(d, d_k))  
 W_value=torch.nn.Parameter(torch.rand(d, d_v))

在这个例子中将dq和dk设置为2，dv设置为4。实际应用中这些维度通常要大得多，这里使用小数值是为了便于理解概念。

通过操作这些矩阵和维度，可以控制模型如何关注输入的不同部分从而捕捉数据中的复杂关系和依赖性。

计算自注意力机制中的非归一化注意力权重

在自注意力机制中，计算非归一化注意力权重是一个关键步骤。下面将以输入序列的第三个元素（索引为2）作为查询来演示这个过程。

首先将这个输入元素投影到查询、键和值空间：

 x_3=embedded_sentence[2]  # 第三个元素（索引2）
 query_3=x_3@W_query  
 key_3=x_3@W_key  
 value_3=x_3@W_value  
 
 print("Query shape:", query_3.shape)  
 print("Key shape:", key_3.shape)  
 print("Value shape:", value_3.shape)

输出：

Query shape: torch.Size([2])  
Key shape: torch.Size([2])  
Value shape: torch.Size([4])

这些形状与我们之前设定的d_q = d_k = 2和d_v = 4相符。接下来计算所有输入元素的键和值：

keys = embedded_sentence @ W_key  
values = embedded_sentence @ W_value  

print("All keys shape:", keys.shape)  
print("All values shape:", values.shape)

输出：

All keys shape: torch.Size([6, 2])  
All values shape: torch.Size([6, 4])

计算非归一化注意力权重。这是通过查询与每个键的点积来实现的。以query_3为例：

omega_3 = query_3 @ keys.T  
print("Unnormalized attention weights for query 3:")  
print(omega_3)

输出：

Unnormalized attention weights for query 3:  
tensor([ 0.8721, -0.5302,  2.1436, -1.7589,  0.9103,  1.3245])

这六个值表示我们的第三个输入（查询）与序列中每个输入的兼容性得分。

为了更好地理解这些得分的含义，我们来看最高和最低的得分：

max_score = omega_3.max()  
min_score = omega_3.min()  
max_index = omega_3.argmax()  
min_index = omega_3.argmin()  

print(f"Highest compatibility: {max_score:.4f} with input {max_index+1}")  
print(f"Lowest compatibility: {min_score:.4f} with input {min_index+1}")  

输出：

Highest compatibility: 2.1436 with input 3  
Lowest compatibility: -1.7589 with input 4

值得注意的是，第三个输入（我们的查询）与自身具有最高的兼容性。这在自注意力中是常见的，因为一个输入通常包含与其自身上下文高度相关的信息。而在这个例子中，第四个输入与我们的查询似乎关联性最低。

这些非归一化的注意力权重提供了一个原始度量，表示每个输入应如何影响我们查询输入的表示。它们捕捉了输入序列不同部分之间的初始关系，为模型理解数据中的复杂依赖关系奠定了基础。

在实际应用中，这些得分会进一步经过处理（如softmax归一化）以得到最终的注意力权重，但这个初始步骤在确定每个输入元素的相对重要性方面起着关键作用。

注意力权重归一化与上下文向量计算

计算非归一化注意力权重（ω）后，自注意力机制的下一个关键步骤是对这些权重进行归一化，并利用它们计算上下文向量。这个过程使模型能够聚焦于输入序列中最相关的部分。

我们首先对非归一化注意力权重进行归一化。使用softmax函数并按1/√(dk)进行缩放，其中dk是键向量的维度：

import torch.nn.functional as F  

d_k = 2  # 键向量的维度  
omega_3 = query_3 @ keys.T  # 使用前面的例子  

attention_weights_3 = F.softmax(omega_3 / d_k**0.5, dim=0)  
print("Normalized attention weights for input 3:")  
print(attention_weights_3)

输出：

Normalized attention weights for input 3:  
tensor([0.1834, 0.0452, 0.6561, 0.0133, 0.1906, 0.2885])

缩放（1/√dk）至关有助于在模型深度增加时维持梯度的合适大小，促进稳定训练。如果没有这种缩放点积可能会变得过大，将softmax函数推入梯度极小的区域。

下面解释这些归一化权重：

max_weight = attention_weights_3.max()  
max_weight_index = attention_weights_3.argmax()  

print(f"Input {max_weight_index+1} has the highest attention weight: {max_weight:.4f}")

输出：

Input 3 has the highest attention weight: 0.6561

可以看到第三个输入（我们的查询）获得了最高的注意力权重，这在自注意力机制中是常见的现象。

最后一步是计算上下文向量。这个向量是值向量的加权和，其中权重是我们归一化的注意力权重：

context_vector_3 = attention_weights_3 @ values  

print("Context vector shape:", context_vector_3.shape)  
print("Context vector:")  
print(context_vector_3)

输出：

Context vector shape: torch.Size([4])  
Context vector:  
tensor([0.6237, 0.9845, 1.0523, 1.2654])

这个上下文向量代表了原始输入（在这里是x(3)）经过所有其他输入信息的丰富，这些信息根据注意力机制确定的相关性进行加权。

我们的上下文向量有4个维度，这与之前选择的dv = 4相匹配。这个维度可以独立于输入维度选择，为模型设计提供了灵活性。

这样就已经将原始输入转换为一个上下文感知的表示。这个向量不仅包含了来自输入本身的信息，还包含了来自整个序列的相关信息，这些信息根据计算出的注意力分数进行加权。这种能够动态关注输入相关部分的能力是Transformer模型在处理序列数据时表现卓越的关键原因。

自注意力的PyTorch实现

为了便于集成到更大的神经网络架构中，可以将自注意力机制封装为一个PyTorch模块。以下是

SelfAttention

类的实现，它包含了我们之前讨论的整个自注意力过程：

import torch  
import torch.nn as nn  

class SelfAttention(nn.Module):  
    def __init__(self, d_in, d_out_kq, d_out_v):  
        super().__init__()  
        self.d_out_kq = d_out_kq  
        self.W_query = nn.Parameter(torch.rand(d_in, d_out_kq))  
        self.W_key = nn.Parameter(torch.rand(d_in, d_out_kq))  
        self.W_value = nn.Parameter(torch.rand(d_in, d_out_v))  

    def forward(self, x):  
        keys = x @ self.W_key  
        queries = x @ self.W_query  
        values = x @ self.W_value  

        attn_scores = queries @ keys.T  
        attn_weights = torch.softmax(  
            attn_scores / self.d_out_kq**0.5, dim=-1  
        )  

        context_vec = attn_weights @ values  
        return context_vec

这个类封装了以下步骤：

1. 将输入投影到键、查询和值空间
2. 计算注意力分数
3. 缩放和归一化注意力权重
4. 生成最终的上下文向量

关键组件说明：

• 在__init__中，我们将权重矩阵初始化为nn.Parameter对象，使PyTorch能够在训练过程中自动跟踪和更新它们。
• forward方法以简洁的方式实现了整个自注意力过程。
• 我们使用@运算符进行矩阵乘法，这等同于torch.matmul。
• 缩放因子self.d_out_kq**0.5在softmax之前应用，如前所述。

使用这个

SelfAttention

模块示例如下：

torch.manual_seed(123)  

d_in, d_out_kq, d_out_v = 3, 2, 4  

sa = SelfAttention(d_in, d_out_kq, d_out_v)  

# 假设embedded_sentence是我们的输入张量  
output = sa(embedded_sentence)  
print(output)

输出：

tensor([[-0.1564,  0.1028, -0.0763, -0.0764],  
        [ 0.5313,  1.3607,  0.7891,  1.3110],  
        [-0.3542, -0.1234, -0.2627, -0.3706],  
        [ 0.0071,  0.3345,  0.0969,  0.1998],  
        [ 0.1008,  0.4780,  0.2021,  0.3674],  
        [-0.5296, -0.2799, -0.4107, -0.6006]], grad_fn=<MmBackward0>)

这个输出张量中的每一行代表相应输入token的上下文向量。值得注意的是，第二行

[0.5313, 1.3607, 0.7891, 1.3110]

与我们之前为第二个输入元素计算的结果一致。

这个实现高效且可并行处理所有输入token。它还具有灵活性，我们可以通过调整

d_out_kq

和

d_out_v

参数轻松改变键/查询和值投影的维度。

多头注意力机制：自注意力的高级扩展

图4：原始Transformer架构中的多头注意力模块

多头注意力机制是对前面探讨的自注意力机制的一个强大扩展。它允许模型在不同位置同时关注来自不同表示子空间的信息。下面我们将详细分析这个概念并实现它。

多头注意力的核心概念

多头注意力机制的主要特点包括：

1. 创建多组查询、键和值权重矩阵。
2. 每组矩阵形成一个"注意力头"。
3. 每个头可能关注输入序列的不同方面。
4. 所有头的输出被连接并进行线性变换，生成最终输出。

这种方法使模型能够同时捕捉数据中的多种类型的关系和模式。

多头注意力的实现

以下是

MultiHeadAttentionWrapper

类的实现，它利用了我们之前定义的

SelfAttention

类：

class MultiHeadAttentionWrapper(nn.Module):  
    def __init__(self, d_in, d_out_kq, d_out_v, num_heads):  
        super().__init__()  
        self.heads = nn.ModuleList(  
            [SelfAttention(d_in, d_out_kq, d_out_v)   
             for _ in range(num_heads)]  
        )  

    def forward(self, x):  
        return torch.cat([head(x) for head in self.heads], dim=-1)

使用这个多头注意力包装器：

torch.manual_seed(123)  

d_in, d_out_kq, d_out_v = 3, 2, 1  
num_heads = 4  

mha = MultiHeadAttentionWrapper(d_in, d_out_kq, d_out_v, num_heads)  

context_vecs = mha(embedded_sentence)  

print(context_vecs)  
print("context_vecs.shape:", context_vecs.shape)

输出：

tensor([[-0.0185,  0.0170,  0.1999, -0.0860],  
        [ 0.4003,  1.7137,  1.3981,  1.0497],  
        [-0.1103, -0.1609,  0.0079, -0.2416],  
        [ 0.0668,  0.3534,  0.2322,  0.1008],  
        [ 0.1180,  0.6949,  0.3157,  0.2807],  
        [-0.1827, -0.2060, -0.2393, -0.3167]], grad_fn=<CatBackward0>)  
context_vecs.shape: torch.Size([6, 4])

多头注意力的优势

1. 多样化特征学习：每个头可以学习关注输入的不同方面。例如，一个头可能专注于局部关系而另一个可能捕捉长距离依赖。
2. 增强模型容量：多个头允许模型表示数据中更复杂的关系，而不显著增加参数数量。
3. 并行处理效率：每个头的独立性使得在GPU或TPU上能进行高效的并行计算。
4. 提高模型稳定性和鲁棒性：使用多个头可以使模型更加鲁棒，因为它不太可能过度拟合单一注意力机制捕捉到的特定模式。

多头注意力与单头大输出的比较

虽然增加单个自注意力头的输出维度（例如，在单个头中设置

d_out_v = 4

）可能看起来与使用多个头相似，但它们之间存在关键差异：

1. 独立学习能力：多头注意力中的每个头学习自己的查询、键和值投影集，允许更多样化的特征提取。
2. 计算效率优势：多头注意力可以更高效地并行化，可能导致更快的训练和推理速度。
3. 集成学习效果：多个头的作用类似于注意力机制的集成，每个头可能专门处理输入的不同方面。

实际应用考虑

在实际应用中，注意力头的数量是一个可调整的超参数。例如，7B参数的Llama 2模型使用32个注意力头。头的数量选择通常取决于特定任务、模型大小和可用的计算资源。

通过利用多头注意力机制，Transformer模型能够捕捉输入数据中的丰富关系集，这是它们在各种自然语言处理任务中表现卓越的关键因素。

交叉注意力：连接不同输入序列的桥梁

交叉注意力是注意力机制的一个强大变体，它允许模型处理来自两个不同输入序列的信息。这在需要一个序列为另一个序列的处理提供信息或指导的场景中特别有用。接下来将深入探讨交叉注意力的概念和实现。

交叉注意力的核心概念

交叉注意力的主要特点包括：

1. 处理两个不同的输入序列。
2. 查询由一个序列生成，而键和值来自另一个序列。
3. 允许模型基于另一个序列的内容有选择地关注一个序列的部分。

交叉注意力的实现

以下是

CrossAttention

类的实现：

class CrossAttention(nn.Module):  
    def __init__(self, d_in, d_out_kq, d_out_v):  
        super().__init__()  
        self.d_out_kq = d_out_kq  
        self.W_query = nn.Parameter(torch.rand(d_in, d_out_kq))  
        self.W_key = nn.Parameter(torch.rand(d_in, d_out_kq))  
        self.W_value = nn.Parameter(torch.rand(d_in, d_out_v))  

    def forward(self, x_1, x_2):  
        queries_1 = x_1 @ self.W_query  
        keys_2 = x_2 @ self.W_key  
        values_2 = x_2 @ self.W_value  

        attn_scores = queries_1 @ keys_2.T  
        attn_weights = torch.softmax(  
            attn_scores / self.d_out_kq**0.5, dim=-1)  

        context_vec = attn_weights @ values_2  
        return context_vec

让我们使用这个交叉注意力模块：

torch.manual_seed(123)  

d_in, d_out_kq, d_out_v = 3, 2, 4  

crossattn = CrossAttention(d_in, d_out_kq, d_out_v)  

first_input = embedded_sentence  
second_input = torch.rand(8, d_in)  

print("First input shape:", first_input.shape)  
print("Second input shape:", second_input.shape)  

context_vectors = crossattn(first_input, second_input)  

print(context_vectors)  
print("Output shape:", context_vectors.shape)

输出：

First input shape: torch.Size([6, 3])  
Second input shape: torch.Size([8, 3])  
tensor([[0.4231, 0.8665, 0.6503, 1.0042],  
        [0.4874, 0.9718, 0.7359, 1.1353],  
        [0.4054, 0.8359, 0.6258, 0.9667],  
        [0.4357, 0.8886, 0.6678, 1.0311],  
        [0.4429, 0.9006, 0.6775, 1.0460],  
        [0.3860, 0.8021, 0.5985, 0.9250]], grad_fn=<MmBackward0>)  
Output shape: torch.Size([6, 4])

交叉注意力与自注意力的主要区别

1. 双输入序列：交叉注意力接受两个输入，x_1和x_2，而不是单一输入。
2. 查询-键交互方式：查询来自x_1，而键和值来自x_2。
3. 序列长度灵活性：两个输入序列可以具有不同的长度。

交叉注意力的应用领域

1. 机器翻译：在原始Transformer模型中，交叉注意力允许解码器在生成翻译时关注源句子的相关部分。
2. 图像描述生成：模型可以在生成描述的每个词时关注图像的不同部分（表示为图像特征序列）。
3. Stable Diffusion模型：交叉注意力用于将图像生成与文本提示相关联，允许模型将文本信息整合到视觉生成过程中。
4. 问答系统：模型可以根据问题的内容关注上下文段落的不同部分。

交叉注意力的优势

1. 信息整合能力：允许模型有选择地将一个序列的信息整合到另一个序列的处理中。
2. 处理多模态输入的灵活性：可以处理不同长度和模态的输入。
3. 增强可解释性：注意力权重可以提供洞察，说明模型如何关联两个序列的不同部分。

实际应用中的考虑因素

• 嵌入维度（d_in）必须对两个输入序列保持一致，即使它们的长度不同。
• 对于长序列，交叉注意力可能计算密集，需要考虑计算效率。
• 与自注意力类似，交叉注意力也可以扩展到多头版本，以获得更强的表达能力。

交叉注意力是一个多功能工具，使模型能够处理来自多个来源或模态的信息，这在许多高级AI应用中至关重要。它能够动态关注不同输入之间的相关信息，这显著促进了模型在需要整合多样信息源的任务中的成功。

Stable Diffusion模型也利用了交叉注意力机制。在该模型中交叉注意力发生在U-Net架构内生成的图像特征和用于指导的文本提示之间。这种技术最初在介绍Stable Diffusion概念的论文《High-Resolution Image Synthesis with Latent Diffusion Models》中被提出。随后Stability AI采用了这种方法来实现广受欢迎的Stable Diffusion模型。

因果自注意力

图7：原始Transformer架构中的因果自注意力模块（来源："Attention Is All You Need"）

我们下面介绍如何将先前探讨的自注意力机制调整为因果自注意力机制，这种机制特别适用于GPT类（解码器风格）的大型语言模型（LLMs）进行文本生成。这种机制也被称为"掩码自注意力"。在原始Transformer架构中，它对应于"掩码多头注意力"模块。为了简化说明将重点关注单个注意力头，但这个概念同样适用于多头注意力。

因果自注意力确保给定位置的输出仅基于序列中前面位置的已知输出，而不依赖于后续位置的信息。简而言之，在预测每个下一个词时，模型应该只考虑之前的词。为了在GPT类LLM中实现这一点，我们对输入文本中每个被处理的token的未来token进行掩码处理。

为了说明这个过程，让我们考虑一个训练文本样本："The cat sits on the mat"。在因果自注意力中，我们会有以下设置，其中箭头右侧的单词的上下文向量应该只包含自身和前面的单词：

"The" → "cat""The cat" → "sits""The cat sits" → "on""The cat sits on" → "the""The cat sits on the" → "mat"

这种设置确保在生成文本时，模型只使用在生成过程的每个步骤中可用的信息。

回顾前面自注意力部分的注意力分数计算：

torch.manual_seed(123)  

d_in, d_out_kq, d_out_v = 3, 2, 4  

W_query = nn.Parameter(torch.rand(d_in, d_out_kq))  
W_key = nn.Parameter(torch.rand(d_in, d_out_kq))  
W_value = nn.Parameter(torch.rand(d_in, d_out_v))  

x = embedded_sentence  

keys = x @ W_key  
queries = x @ W_query  
values = x @ W_value  

attn_scores = queries @ keys.T   

print(attn_scores)  
print(attn_scores.shape)

输出：

tensor([[ 0.0613, -0.3491,  0.1443, -0.0437, -0.1303,  0.1076],  
        [-0.6004,  3.4707, -1.5023,  0.4991,  1.2903, -1.3374],  
        [ 0.2432, -1.3934,  0.5869, -0.1851, -0.5191,  0.4730],  
        [-0.0794,  0.4487, -0.1807,  0.0518,  0.1677, -0.1197],  
        [-0.1510,  0.8626, -0.3597,  0.1112,  0.3216, -0.2787],  
        [ 0.4344, -2.5037,  1.0740, -0.3509, -0.9315,  0.9265]],  
       grad_fn=<MmBackward0>)  
torch.Size([6, 6])

得到了一个6x6的张量，表示6个输入token的成对非归一化注意力权重（注意力分数）。

接下来通过softmax函数计算缩放点积注意力：

attn_weights = torch.softmax(attn_scores / d_out_kq**0.5, dim=1)  
print(attn_weights)

输出：

tensor([[0.1772, 0.1326, 0.1879, 0.1645, 0.1547, 0.1831],  
        [0.0386, 0.6870, 0.0204, 0.0840, 0.1470, 0.0229],  
        [0.1965, 0.0618, 0.2506, 0.1452, 0.1146, 0.2312],  
        [0.1505, 0.2187, 0.1401, 0.1651, 0.1793, 0.1463],  
        [0.1347, 0.2758, 0.1162, 0.1621, 0.1881, 0.1231],  
        [0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],  
       grad_fn=<SoftmaxBackward0>)

要实现因果自注意力，需要掩盖所有未来的token。最直接的方法是在对角线上方对注意力权重矩阵应用掩码。我们可以使用PyTorch的tril函数来实现这一点：

block_size = attn_scores.shape[0]  
mask_simple = torch.tril(torch.ones(block_size, block_size))  
print(mask_simple)

输出：

tensor([[1., 0., 0., 0., 0., 0.],  
        [1., 1., 0., 0., 0., 0.],  
        [1., 1., 1., 0., 0., 0.],  
        [1., 1., 1., 1., 0., 0.],  
        [1., 1., 1., 1., 1., 0.],  
        [1., 1., 1., 1., 1., 1.]])

现在将注意力权重与这个掩码相乘，以将对角线上方的所有注意力权重置零：

masked_simple = attn_weights * mask_simple  
print(masked_simple)

输出：

tensor([[0.1772, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],  
        [0.0386, 0.6870, 0.0000, 0.0000, 0.0000, 0.0000],  
        [0.1965, 0.0618, 0.2506, 0.0000, 0.0000, 0.0000],  
        [0.1505, 0.2187, 0.1401, 0.1651, 0.0000, 0.0000],  
        [0.1347, 0.2758, 0.1162, 0.1621, 0.1881, 0.0000],  
        [0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],  
       grad_fn=<MulBackward0>)

但是这种方法导致每一行的注意力权重之和不再等于1。为了解决这个问题还需要对行进行归一化：

row_sums = masked_simple.sum(dim=1, keepdim=True)  
masked_simple_norm = masked_simple / row_sums  
print(masked_simple_norm)

输出：

tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],  
        [0.0532, 0.9468, 0.0000, 0.0000, 0.0000, 0.0000],  
        [0.3862, 0.1214, 0.4924, 0.0000, 0.0000, 0.0000],  
        [0.2232, 0.3242, 0.2078, 0.2449, 0.0000, 0.0000],  
        [0.1536, 0.3145, 0.1325, 0.1849, 0.2145, 0.0000],  
        [0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],  
       grad_fn=<DivBackward0>)

现在每一行的注意力权重之和都等于1，符合注意力权重的标准规范。

有一种更高效的方法来实现相同的结果，可以在应用softmax之前对注意力分数进行掩码，而不是在之后对注意力权重进行掩码：

mask = torch.triu(torch.ones(block_size, block_size), diagonal=1)  
masked = attn_scores.masked_fill(mask.bool(), float('-inf'))  
print(masked)

输出：

tensor([[ 0.0613,    -inf,    -inf,    -inf,    -inf,    -inf],  
        [-0.6004,  3.4707,    -inf,    -inf,    -inf,    -inf],  
        [ 0.2432, -1.3934,  0.5869,    -inf,    -inf,    -inf],  
        [-0.0794,  0.4487, -0.1807,  0.0518,    -inf,    -inf],  
        [-0.1510,  0.8626, -0.3597,  0.1112,  0.3216,    -inf],  
        [ 0.4344, -2.5037,  1.0740, -0.3509, -0.9315,  0.9265]],  
       grad_fn=<MaskedFillBackward0>)

现在应用softmax来获得最终的注意力权重：

attn_weights = torch.softmax(masked / d_out_kq**0.5, dim=1)  
print(attn_weights)

输出：

tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],  
        [0.0532, 0.9468, 0.0000, 0.0000, 0.0000, 0.0000],  
        [0.3862, 0.1214, 0.4924, 0.0000, 0.0000, 0.0000],  
        [0.2232, 0.3242, 0.2078, 0.2449, 0.0000, 0.0000],  
        [0.1536, 0.3145, 0.1325, 0.1849, 0.2145, 0.0000],  
        [0.1973, 0.0247, 0.3102, 0.1132, 0.0751, 0.2794]],  
       grad_fn=<SoftmaxBackward0>)

这种方法更加高效，因为它避免了对掩码位置进行不必要的计算，并且不需要重新归一化。softmax函数有效地将-inf值视为零概率，因为e^(-inf)趋近于0。

通过这种方式实现因果自注意力可以确保了语言模型能够以从左到右的方式生成文本，在预测每个新token时只考虑先前的上下文。这对于在文本生成任务中产生连贯和上下文适当的序列至关重要。

总结

在本文中，我们深入探讨了自注意力机制的内部工作原理，通过实际编码来理解其实现。并以此为基础研究了多头注意力，这是大型语言Transformer模型的核心组件。

我们还扩展了讨论范围，探索了交叉注意力（自注意力的一个变体），特别适用于两个不同序列之间的信息交互。这种机制在机器翻译或图像描述等任务中特别有用，其中一个领域的信息需要指导另一个领域的处理。

最后，深入研究了因果自注意力，这是解码器风格LLM（如GPT和Llama）生成连贯和上下文适当序列的关键概念。这种机制确保模型的预测仅基于先前的token，模仿自然语言生成的从左到右的特性。

最后：本文中呈现的代码主要用于说明目的。在实际训练LLM时，自注意力的实现通常使用优化版本。例如，Flash Attention等技术显著减少了内存占用和计算负载，使大型模型的训练更加高效。

作者：Tejaswi kashyap