用Pytorch搭建一个房价预测模型

本文参加新星计划人工智能(Pytorch)赛道：https://bbs.csdn.net/topics/613989052

一、项目介绍

    在此项目中，目的是预测爱荷华州Ames的房价，给定81个特征，描述了房子、面积、土地、基础设施、公共设施等。埃姆斯数据集具有分类和连续特征的良好组合，大小适中，也许最重要的是，它不像其他类似的数据集（如波士顿住房）那样存在潜在的红线或数据输入问题。在这里我将主要讨论PyTorch建模的相关方面，作为一点额外的内容，我还将演示PyTorch中开发的模型的神经元重要性。你可以在PyTorch中尝试不同的网络架构或模型类型。本项目中的重点是方法论，而不是详尽地寻找最佳解决方案。

二、准备工作

为了准备这个项目，我们首先需要下载数据，并通过以下步骤进行一些预处理。

from sklearn.datasets import fetch_openml
data = fetch_openml(data_id=42165, as_frame=True)

关于该数据集的完整描述，你可以去该网址查看：https://www.openml.org/d/42165。

查看数据特征

import pandas as pd
data_ames = pd.DataFrame(data.data, columns=data.feature_names)
data_ames['SalePrice'] = data.target
data_ames.info()

下面是DataFrame的信息

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1460 entries, 0 to 1459
Data columns (total 81 columns):
Id               1460 non-null float64
MSSubClass       1460 non-null float64
MSZoning         1460 non-null object
LotFrontage      1201 non-null float64
LotArea          1460 non-null float64
Street           1460 non-null object
Alley            91 non-null object
LotShape         1460 non-null object
LandContour      1460 non-null object
Utilities        1460 non-null object
LotConfig        1460 non-null object
LandSlope        1460 non-null object
Neighborhood     1460 non-null object
Condition1       1460 non-null object
Condition2       1460 non-null object
BldgType         1460 non-null object
HouseStyle       1460 non-null object
OverallQual      1460 non-null float64
OverallCond      1460 non-null float64
YearBuilt        1460 non-null float64
YearRemodAdd     1460 non-null float64
RoofStyle        1460 non-null object
RoofMatl         1460 non-null object
Exterior1st      1460 non-null object
Exterior2nd      1460 non-null object
MasVnrType       1452 non-null object
MasVnrArea       1452 non-null float64
ExterQual        1460 non-null object
ExterCond        1460 non-null object
Foundation       1460 non-null object
BsmtQual         1423 non-null object
BsmtCond         1423 non-null object
BsmtExposure     1422 non-null object
BsmtFinType1     1423 non-null object
BsmtFinSF1       1460 non-null float64
BsmtFinType2     1422 non-null object
BsmtFinSF2       1460 non-null float64
BsmtUnfSF        1460 non-null float64
TotalBsmtSF      1460 non-null float64
Heating          1460 non-null object
HeatingQC        1460 non-null object
CentralAir       1460 non-null object
Electrical       1459 non-null object
1stFlrSF         1460 non-null float64
2ndFlrSF         1460 non-null float64
LowQualFinSF     1460 non-null float64
GrLivArea        1460 non-null float64
BsmtFullBath     1460 non-null float64
BsmtHalfBath     1460 non-null float64
FullBath         1460 non-null float64
HalfBath         1460 non-null float64
BedroomAbvGr     1460 non-null float64
KitchenAbvGr     1460 non-null float64
KitchenQual      1460 non-null object
TotRmsAbvGrd     1460 non-null float64
Functional       1460 non-null object
Fireplaces       1460 non-null float64
FireplaceQu      770 non-null object
GarageType       1379 non-null object
GarageYrBlt      1379 non-null float64
GarageFinish     1379 non-null object
GarageCars       1460 non-null float64
GarageArea       1460 non-null float64
GarageQual       1379 non-null object
GarageCond       1379 non-null object
PavedDrive       1460 non-null object
WoodDeckSF       1460 non-null float64
OpenPorchSF      1460 non-null float64
EnclosedPorch    1460 non-null float64
3SsnPorch        1460 non-null float64
ScreenPorch      1460 non-null float64
PoolArea         1460 non-null float64
PoolQC           7 non-null object
Fence            281 non-null object
MiscFeature      54 non-null object
MiscVal          1460 non-null float64
MoSold           1460 non-null float64
YrSold           1460 non-null float64
SaleType         1460 non-null object
SaleCondition    1460 non-null object
SalePrice        1460 non-null float64
dtypes: float64(38), object(43)
memory usage: 924.0+ KB

接下来，我们还将使用一个库，即 captum，它可以检查 PyTorch 模型的特征和神经元重要性。

pip install captum

在做完这些准备工作后，我们来看看如何预测房价。

三、实验过程

3.1数据预处理

    在这里，首先要进行数据缩放处理，因为所有的变量都有不同的尺度。分类变量需要转换为数值类型，以便将它们输入到我们的模型中。我们可以选择一热编码，即我们为每个分类因子创建哑变量，或者是序数编码，即我们对所有因子进行编号，并用这些数字替换字符串。我们可以像其他浮动变量一样将虚拟变量送入，而序数编码则需要使用嵌入，即线性神经网络投影，在多维空间中对类别进行重新排序。我们在这里采取嵌入的方式。

import numpy as np
from category_encoders.ordinal import OrdinalEncoder
from sklearn.preprocessing import StandardScaler

num_cols = list(data_ames.select_dtypes(include='float'))
cat_cols = list(data_ames.select_dtypes(include='object'))

ordinal_encoder = OrdinalEncoder().fit(
    data_ames[cat_cols]
)
standard_scaler = StandardScaler().fit(
    data_ames[num_cols]
)

X = pd.DataFrame(
    data=np.column_stack([
        ordinal_encoder.transform(data_ames[cat_cols]),
        standard_scaler.transform(data_ames[num_cols])
    ]),
    columns=cat_cols + num_cols
)

3.2拆分数据集

   在构建模型之前，我们需要将数据拆分为训练集和测试集。在这里，我们添加了一个数值变量的分层。这可以确保不同的部分（其中五个）在训练集和测试集中都以同等的数量包含。

np.random.seed(12)  
from sklearn.model_selection import train_test_split

bins = 5
sale_price_bins = pd.qcut(
    X['SalePrice'], q=bins, labels=list(range(bins))
)
X_train, X_test, y_train, y_test = train_test_split(
    X.drop(columns='SalePrice'),
    X['SalePrice'],
    random_state=12,
    stratify=sale_price_bins
)

3.3构建PyTorch模型

    接下来开始建立我们的PyTorch模型。我们将使用PyTorch实现一个具有批量输入的神经网络回归，具体将涉及以下步骤。

• 1. 将数据转换为Torch tensors
• 1. 定义模型结构
• 1. 定义损失标准和优化器。
• 1. 创建一个批次的数据加载器
• 1. 跑步训练

3.3.1.数据转换

首先将数据转换为torch tensors

from torch.autograd import Variable 

num_features = list(
    set(num_cols) - set(['SalePrice', 'Id'])
)
X_train_num_pt = Variable(
    torch.cuda.FloatTensor(
        X_train[num_features].values
    )
)
X_train_cat_pt = Variable(
    torch.cuda.LongTensor(
        X_train[cat_cols].values
    )
)
y_train_pt = Variable(
    torch.cuda.FloatTensor(y_train.values)
).view(-1, 1)
X_test_num_pt = Variable(
    torch.cuda.FloatTensor(
        X_test[num_features].values
    )
)
X_test_cat_pt = Variable(
   torch.cuda.LongTensor(
        X_test[cat_cols].values
    ).long()
)
y_test_pt = Variable(
    torch.cuda.FloatTensor(y_test.values)
).view(-1, 1)

    这可以确保我们将数字和分类数据加载到单独的变量中，类似于NumPy。如果你把数据类型混合在一个变量（数组/矩阵）中，它们就会变成对象。我们希望把数值变量弄成浮点数，把分类变量弄成长（或int），索引我们的类别。我们还将训练集和测试集分开。显然，一个ID变量在模型中不应该是重要的。在最坏的情况下，如果ID与目标有任何相关性，它可能会引入目标泄漏。我们已经把它从这一步的处理中删除了。

3.3.2定义模型架构

class RegressionModel(torch.nn.Module): 
  
    def __init__(self, X, num_cols, cat_cols, device=torch.device('cuda'), embed_dim=2, hidden_layer_dim=2, p=0.5): 
        super(RegressionModel, self).__init__() 
        self.num_cols = num_cols
        self.cat_cols = cat_cols
        self.embed_dim = embed_dim
        self.hidden_layer_dim = hidden_layer_dim
        
        self.embeddings = [
            torch.nn.Embedding(
                num_embeddings=len(X[col].unique()),
                embedding_dim=embed_dim
            ).to(device)
            for col in cat_cols
        ]
        hidden_dim = len(num_cols) + len(cat_cols) * embed_dim,
        
        # hidden layer
        self.hidden = torch.nn.Linear(torch.IntTensor(hidden_dim), hidden_layer_dim).to(device)
        self.dropout_layer = torch.nn.Dropout(p=p).to(device)
        self.hidden_act = torch.nn.ReLU().to(device)
        
        # output layer
        self.output = torch.nn.Linear(hidden_layer_dim, 1).to(device)
    
    def forward(self, num_inputs, cat_inputs):
        '''Forward method with two input variables -
        numeric and categorical.
        '''
        cat_x = [
            torch.squeeze(embed(cat_inputs[:, i] - 1))
            for i, embed in enumerate(self.embeddings)
        ]
        x = torch.cat(cat_x + [num_inputs], dim=1)
        x = self.hidden(x)
        x = self.dropout_layer(x)
        x = self.hidden_act(x)
        y_pred = self.output(x)
        return y_pred

house_model = RegressionModel(
    data_ames, num_features, cat_cols
)

    我们在两个线性层（上的激活函数是整流线性单元激活（ReLU）函数。这里需要注意的是，我们不可能将相同的架构（很容易）封装成一个顺序模型，因为分类和数值类型上发生的操作不同。

3.3.3定义损失准则和优化器

    接下来，定义损失准则和优化器。我们将均方误差（MSE）作为损失，随机梯度下降作为我们的优化算法。

criterion = torch.nn.MSELoss().to(device)
optimizer = torch.optim.SGD(house_model.parameters(), lr=0.001)

3.3.4创建数据加载器

现在，创建一个数据加载器，每次输入一批数据。

data_batch = torch.utils.data.TensorDataset(
    X_train_num_pt, X_train_cat_pt, y_train_pt
)
dataloader = torch.utils.data.DataLoader(
    data_batch, batch_size=10, shuffle=True
)

我们设置了10个批次的大小，接下来我们可以进行训练了。

3.3.5.训练模型

   基本上，我们要在epoch上循环，在每个epoch内推理出性能，计算出误差，优化器根据误差进行调整。这是在没有训练的内循环的情况下，在epochs上的循环。

from tqdm.notebook import trange

train_losses, test_losses = [], []
n_epochs = 30
for epoch in trange(n_epochs):
    train_loss, test_loss = 0, 0
  
    # print the errors in training and test:
    if epoch % 10 == 0 :
        print(
            'Epoch: {}/{}\t'.format(epoch, 1000),
            'Training Loss: {:.3f}\t'.format(
                train_loss / len(dataloader)
            ),
            'Test Loss: {:.3f}'.format(
                test_loss / len(dataloader)
            )
        )

训练是在这个循环里面对所有批次的训练数据进行的。

for (x_train_num_batch,x_train_cat_batch,y_train_batch) in dataloader:
        (x_train_num_batch,x_train_cat_batch, y_train_batch) = (
                x_train_num_batch.to(device),
                x_train_cat_batch.to(device),
                y_train_batch.to(device))
        pred_ytrain = house_model.forward(x_train_num_batch, x_train_cat_batch)
        loss = torch.sqrt(criterion(pred_ytrain, y_train_batch)) 

        optimizer.zero_grad() 
        loss.backward() 
        optimizer.step()
        train_loss += loss.item()
        with torch.no_grad():
            house_model.eval()
            pred_ytest = house_model.forward(X_test_num_pt, X_test_cat_pt)
            test_loss += torch.sqrt(criterion(pred_ytest, y_test_pt))

        train_losses.append(train_loss / len(dataloader))
        test_losses.append(test_loss / len(dataloader))

训练结果如下：

我们取 nn.MSELoss 的平方根，因为 PyTorch 中 nn.MSELoss 的定义如下：

((input-target)**2).mean()

绘制一下我们的模型在训练期间对训练和验证数据集的表现。

plt.plot(
    np.array(train_losses).reshape((n_epochs, -1)).mean(axis=1),
    label='Training loss'
)
plt.plot(
    np.array(test_losses).reshape((n_epochs, -1)).mean(axis=1),
    label='Validation loss'
)
plt.legend(frameon=False)
plt.xlabel('epochs')
plt.ylabel('MSE')

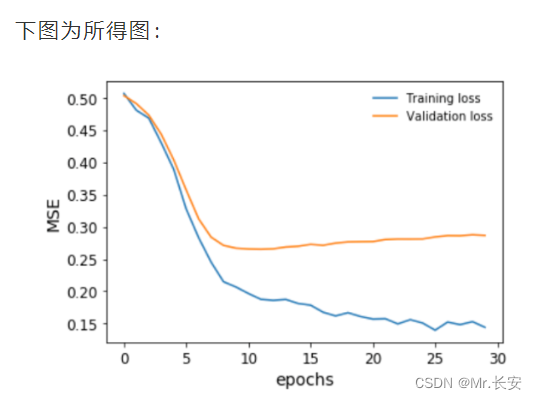
    在我们的验证损失停止下降之前，我们及时停止了训练。我们还可以对目标变量进行排序和bin，并将预测结果与之对比绘制，以便了解模型在整个房价范围内的表现。这是为了避免回归中的情况，尤其是用MSE作为损失，即你只对一个中值范围的预测很好，接近平均值，但对其他任何东西都做得不好。

    我们可以看到，事实上，这个模型在整个房价范围内的预测非常接近。事实上，我们得到的Spearman秩相关度约为93%，具有非常高的显著性，这证实了这个模型的表现具有很高的准确性。

四、原理讲解

    深度学习神经网络框架使用不同的优化算法。其中流行的有随机梯度下降（SGD）、均方根推进（RMSProp）和自适应矩估计（ADAM）。我们定义了随机梯度下降作为我们的优化算法。另外，我们还可以定义其他优化器。

opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.6)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.1)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.8, 0.98))

    SGD的工作原理与梯度下降相同，只是它每次只在一个例子上工作。有趣的是，收敛性与梯度下降相似，并且更容易占用计算机内存。

    RMSProp的工作原理是根据梯度符号来调整算法的学习率。最简单的变体是检查最后两个梯度符号，然后调整学习率，如果它们相同，则增加一个分数，如果它们不同，则减少一个分数。

    ADAM是最流行的优化器之一。它是一种自适应学习算法，根据梯度的第一和第二时刻改变学习率。

    Captum是一个工具，可以帮助我们了解在数据集上学习的神经网络模型的来龙去脉。它可以帮助我们学习以下内容。

• 特征重要性

• 层级重要性

• 神经元的重要性

    这在学习可解释的神经网络中是非常重要的。在这里，综合梯度已经被应用于理解特征重要性。之后，还用层传导法来证明神经元的重要性。
  

五、补充

    既然我们已经定义并训练了我们的神经网络，那么让我们使用 captum 库找到重要的特征和神经元。

from captum.attr import (
    IntegratedGradients,
    LayerConductance,
    NeuronConductance
)
house_model.cpu()
for embedding in house_model.embeddings:
    embedding.cpu()

house_model.cpu()
ing_house = IntegratedGradients(forward_func=house_model.forward, )
#X_test_cat_pt.requires_grad_()
X_test_num_pt.requires_grad_()
attr, delta = ing_house.attribute(
 X_test_num_pt.cpu(),
 target=None,
 return_convergence_delta=True,
 additional_forward_args=X_test_cat_pt.cpu()
)
attr = attr.detach().numpy()

现在，我们有了一个NumPy的特征重要性数组。层和神经元的重要性也可以用这个工具获得。让我们来看看我们第一层的神经元importances。我们可以传递house_model.act1，这是第一层线性层上面的ReLU激活函数。

cond_layer1 = LayerConductance(house_model, house_model.act1)
cond_vals = cond_layer1.attribute(X_test, target=None)
cond_vals = cond_vals.detach().numpy()
df_neuron = pd.DataFrame(data = np.mean(cond_vals, axis=0), columns=['Neuron Importance'])
df_neuron['Neuron'] = range(10)

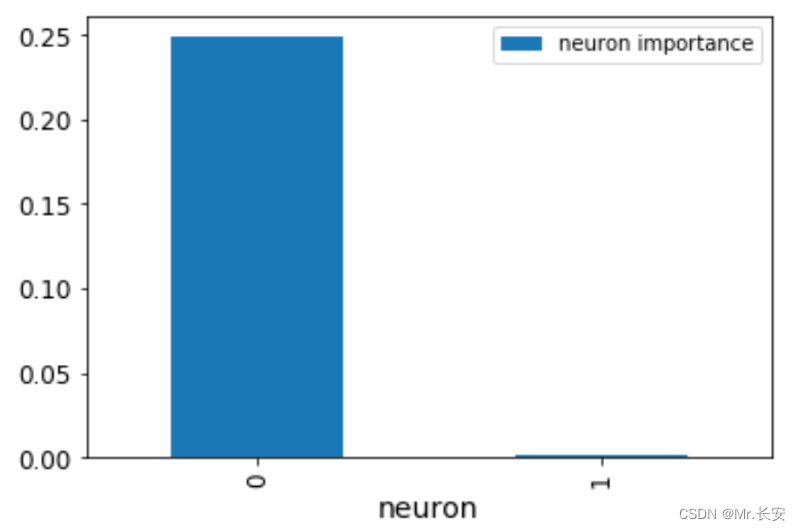
这张图显示了神经元的重要性。显然，一个神经元就是不重要的。我们还可以通过对之前得到的NumPy数组进行排序，看到最重要的变量。

df_feat = pd.DataFrame(np.mean(attr, axis=0), columns=['feature importance'] )
df_feat['features'] = num_features
df_feat.sort_values(
    by='feature importance', ascending=False
).head(10)

这里列出了10个最重要的变量

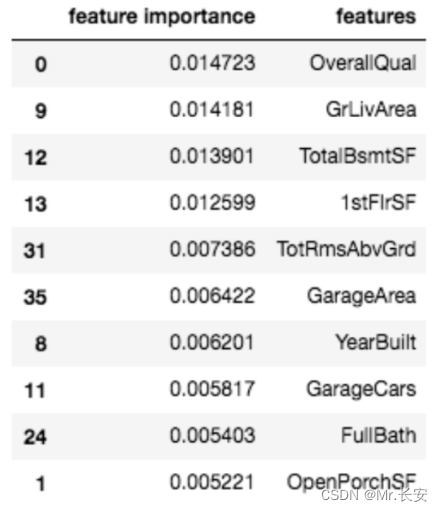
    通常情况下，特征导入可以帮助我们既理解模型，又修剪我们的模型，使其变得不那么复杂（希望减少过度拟合）。