深度学习参数初始化（一）Xavier初始化 含代码

深度学习参数初始化系列：

（一）Xavier初始化 含代码

（二）Kaiming初始化 含代码

一、简介

    网络训练的过程中, 容易出现梯度消失(梯度特别的接近0)和梯度爆炸(梯度特别的大)的情况,导致大部分反向传播得到的梯度不起作用或者起反作用. 研究人员希望能够有一种好的权重初始化方法: 让网络前向传播或者反向传播的时候, 卷积的输出和前传的梯度比较稳定. 合理的方差既保证了数值一定的不同, 又保证了数值一定的稳定.(通过卷积权重的合理初始化, 让计算过程中的数值分布稳定)

    Xavier初始化也称为Glorot初始化，因为发明人为Xavier Glorot。Xavier initialization是 Glorot 等人为了解决随机初始化的问题提出来的另一种初始化方法，他们的思想就是尽可能的让输入和输出服从相同的分布，这样就能够避免后面层的激活函数的输出值趋向于0。

    因为权重多使用高斯或均匀分布初始化，而两者不会有太大区别，只要保证两者的方差一样就可以了，所以高斯和均匀分布我们一起说。

    Pytorch中已经有实现，下面会详细介绍：

torch.nn.init.xavier_uniform_(tensor: Tensor, gain: float = 1.)
torch.nn.init.xavier_normal_(tensor: Tensor, gain: float = 1.)

二、基础知识

   1. 均匀分布的方差：

    ![gif.latex?Var%20%3D%20%5Cfrac%7B%28b-a%29%5E%7B2%7D%7D%7B12%7D](https://latex.codecogs.com/gif.latex?Var%20%3D%20%5Cfrac%7B%28b-a%29%5E%7B2%7D%7D%7B12%7D)

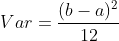
   2.假设随机变量X和随机变量Y相互独立，则有

** **3.假设随机变量X和随机变量Y相互独立，且E(X)=E(Y)=0，则有

    ![gif.latex?Var%28X*Y%29%20%3D%20Var%28X%29*Var%28Y%29](https://latex.codecogs.com/gif.latex?Var%28X*Y%29%20%3D%20Var%28X%29*Var%28Y%29)

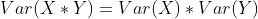
三、标准初始化方法

     权重初始化满足均匀分布时：

    因为上式的方差是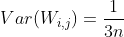：![gif.latex?Var%28W_%7Bi%2Cj%7D%29%3D%5Cfrac%7B1%7D%7B3n%7D](https://latex.codecogs.com/gif.latex?Var%28W_%7Bi%2Cj%7D%29%3D%5Cfrac%7B1%7D%7B3n%7D)，所以对应的高斯分布写作：

    对于全连接网络，我们把输入X的每一维度x看做一个随机变量，并且假设E(x)=0，Var(x)=1。假设权重W和输入X相互独立，则隐层状态的方差为：

    可以看出标准初始化方法得到一个非常好的特性：隐层的状态的均值为0，方差为常量1/3，和网络的层数无关，这意味着对于sigmoid这样的函数来说，自变量落在有梯度的范围内。

    但是因为sigmoid激活值都是大于0的，会导致下一层的输入不满足E(x)=0。其实标准初始化也只适用于满足下面将要提到的Glorot假设的激活函数，比如tanh。

四、Xavier初始化的假设条件

    在文章开始部分我们给出了参数初始化的必要条件。但是这两个条件只保证了训练过程中可以学到有用的信息——参数梯度不为0（因为参数被控制在激活函数的有效区域）。而Glorot认为：优秀的初始化应该使得各层的激活值和状态梯度的方差在传播过程中的方差保持一致。也就是说我们要保证前向传播各层参数的方差和反向传播时各层参数的方差一致 ：

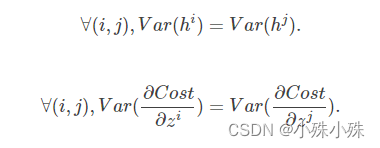
我们把这两个条件称为Glorot条件。

综合起来，现在我们做如下假设：

1.输入的每个特征方差一样：Var(x)；
2.激活函数对称：这样就可以假设每层的输入均值都是0；
3.f′(0)=1
4.初始时，状态值落在激活函数的线性区域：f′(Si(k))≈1。
后三个都是关于激活函数的假设，我们称为Glorot激活函数假设。

五、Xavier初始化的简单的公式推导：

首先给出关于状态的梯度和关于参数的梯度的表达式：

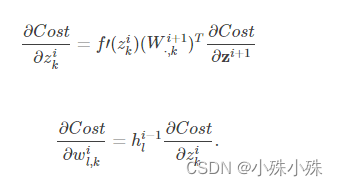
我们以全连接的一层为例，表达式为：

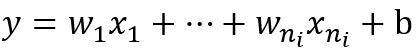
其中ni表示输入个数。

根据概率统计知识我们有下面的方差公式：

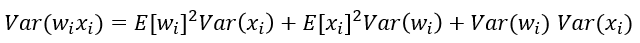
特别的，当我们假设输入和权重都是0均值时（目前有了BN之后，这一点也较容易满足），上式可以简化为：

假设输入x和权重w独立同分布，为了保证输入与输出方差一致，则应该有：

对于一个多层的网络，某一层的方差可以用累积的形式表达，为当前层数：

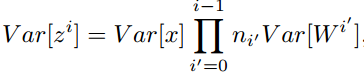
特别的，反向传播计算梯度时同样具有类似的形式：

综上，为了保证前向传播和反向传播时每一层的方差一致，应满足：

但是，实际当中输入与输出的个数往往不相等，于是为了均衡考量，我们将输入输出l两层的方差取均值，最终我们的权重方差应满足：

所以Xavier初始化的高斯分布公式：

根据均匀分布的方差公式:

又因为这里|a|=|b|,所以Xavier初始化的实现就是下面的均匀分布：

六、Pytorch实现：

import torch

# 定义模型 三层卷积 一层全连接
class DemoNet(torch.nn.Module):
    def __init__(self):
        super(DemoNet, self).__init__()
        self.conv1 = torch.nn.Conv2d(1, 1, 3)
        print('random init:', self.conv1.weight)
        '''
        xavier 初始化方法中服从均匀分布 U(−a,a) ，分布的参数 a = gain * sqrt(6/fan_in+fan_out)，
        这里有一个 gain，增益的大小是依据激活函数类型来设定,该初始化方法，也称为 Glorot initialization
        '''
        torch.nn.init.xavier_uniform_(self.conv1.weight, gain=1)
        print('xavier_uniform_:', self.conv1.weight)
        '''
            xavier 初始化方法中服从正态分布，
            mean=0,std = gain * sqrt(2/fan_in + fan_out)
        '''
        torch.nn.init.xavier_normal_(self.conv1.weight, gain=1)
        print('xavier_uniform_:', self.conv1.weight)

if __name__ == '__main__':
    demoNet = DemoNet()

七、对比实验

实验使用tanh为激活函数

1.各层激活值直方图

    上图是原始的初始化，下图是Xavier初始化。Xavier初始化的网络的各层的激活值较为一致，且取值均比原始的标准初始化要小。

2.各层反向传播的梯度（关于状态的梯度）的分布情况

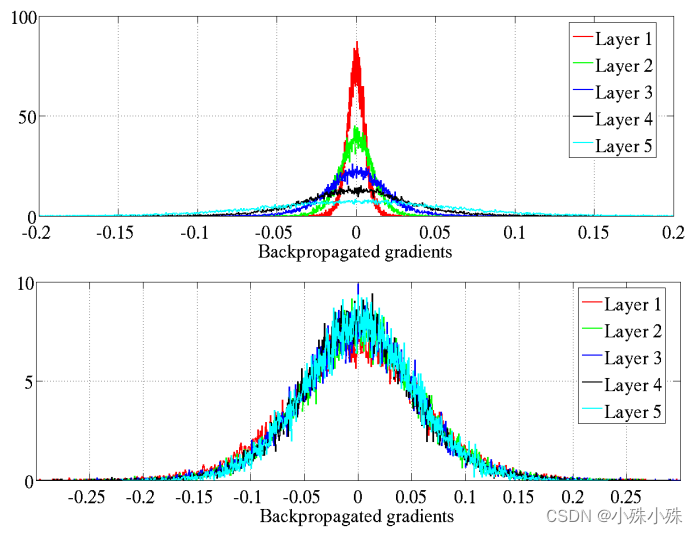
上图是原始的初始化，下图是Xavier初始化。Xavier初始化的网络的各层的梯度较为一致，且取值均比原始的标准初始化要小。作者怀疑不同层上具有不同的梯度可能会导致病态或训练较慢 。

3.各层参数梯度的分布情况

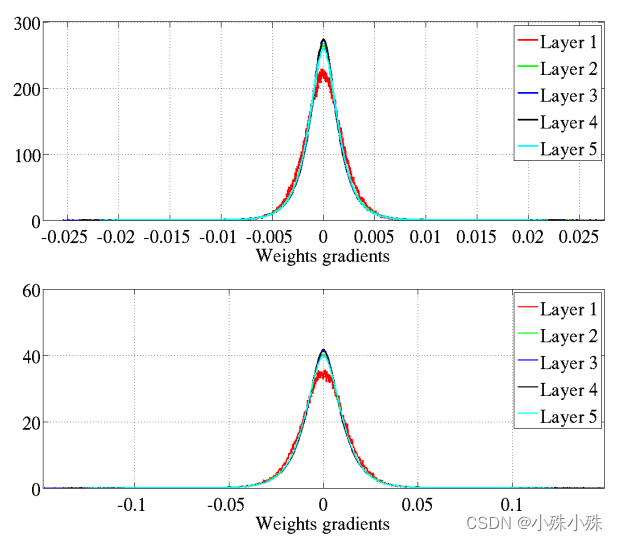
    式子（3）已经证明各层参数梯度的方差和层数基本无关。上图是原始的初始化，下图是Xavier初始化。我们发现下图的标准初始化参数梯度小了一个数量级。

4.各层权重梯度方差的分布情况

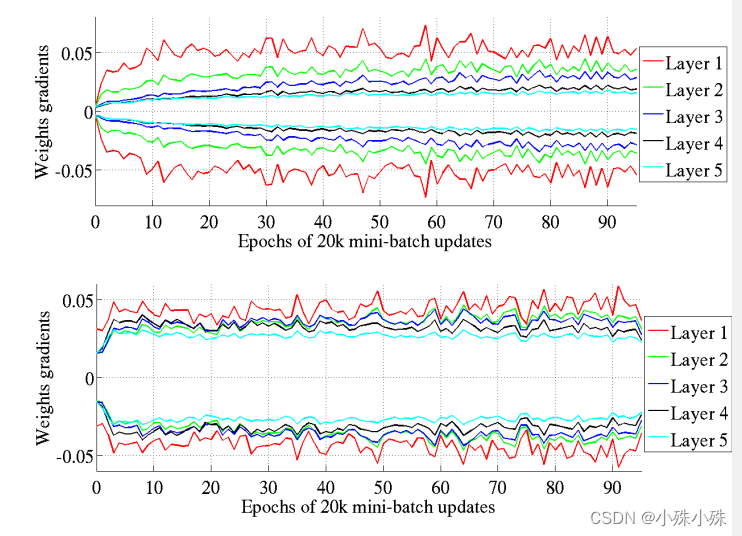
上图是原始的初始化，下图是Xavier初始化。Xavier初始化权重梯度的方差比较一致。

八、总结

1.Xavier初始化的高斯分布公式：

2.Xavier初始化的均匀分布公式：

3.Xavier初始化是在标准初始化方法的基础上，兼顾了各层在前向传播和分享传播时的参数方差。

4.Xavier初始的缺点：因为Xavier的推导过程是基于几个假设的，其中一个是激活函数是线性的。这并不适用于ReLU激活函数。另一个是激活值关于0对称，这个不适用于sigmoid函数和ReLU函数。在使用sigmoid函数和ReLU函数时，标准初始化和Xavier初始化得到的初始激活、参数梯度特性是一样的。激活值的方差逐层递减，参数梯度的方差也逐层递减。