前言:本文的个别内容、图片出自各个博客,但是因时间较久目前找不到原作者链接,如有需要,烦请各位原作者联系我。
一、什么是膨胀卷积?为什么要用膨胀卷积
膨胀卷积(最早由MULTI-SCALE CONTEXT AGGREGATION BY DILATED CONVOLUTIONS(基于膨胀卷积的多尺度上下文融合.2015))
最初的提出是为了解决图像分割的问题而提出的,常见的图像分割算法通常使用池化层和卷积层来增加感受野(Receptive Filed),同时也缩小了特征图尺寸(resolution),然后再利用上采样还原图像尺寸,特征图缩小再放大的过程造成了精度上的损失,因此需要一种操作可以在增加感受野的同时保持特征图的尺寸不变,从而代替下采样和上采样操作。
二、膨胀卷积的特点(优点)
①保持参数个数不变的情况下增大了卷积核的感受野,让每个卷积输出都包含较大范围的信息;
②同时它可以保证输出的特征映射(feature map)的大小保持不变。
三、膨胀卷积特点的理解
1、先看特点②:可以保证输出的特征映射(feature map)的大小保持不变
对于一维信号来说:
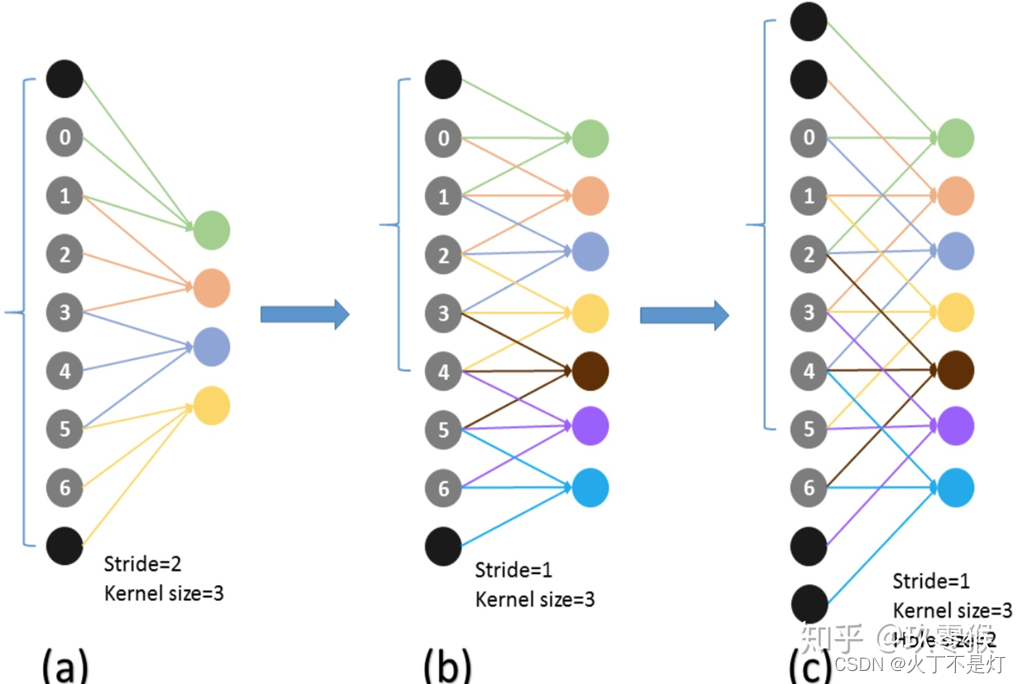
拿一维信号来看,黑色代表padding
(a)是普通的卷积,步长2,卷积核3
(b)是普通卷积,步长1,卷积核3,可以看到输入特征为7个,经过线性加权求和之后,输出的特征为7个
(c)是膨胀卷积,步长1,卷积核3,膨胀率2,可以看到输入特征为7个,经过线性加权求和之后,输出的特征为7个
可以看出经过膨胀卷积输出的特征映射(feature map)的大小和普通卷积一致,保持不变,有无空洞卷积,并不影响输出特征图的尺寸,也就是说输出特征图的尺寸和空洞数无关。
对于二维信号来说:
影响输出特征图尺寸的因素有输入特征图的尺寸 (H,W) ,卷积核的大小 (FH,FW) ,填充 P ,步长 S
设输出特征图尺寸(OH,OW)
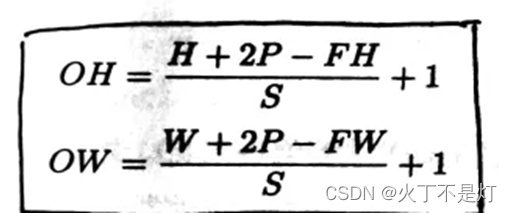
有无空洞卷积,并不影响输出特征图的尺寸,也就是说输出特征图的尺寸和空洞数无关。
2、膨胀卷积特点1:增大了卷积核的感受野

普通卷积3×3

膨胀卷积3×3
从上面两个图可以看出,卷积核不变,但是其感受野明显变化
2.1膨胀处理后的等效卷积核

kernel size=3, stride=1 且 dilation rate 分别为 1, 2
设膨胀卷积的卷积核大小 kernel size = k,膨胀率/空洞数 dilated rate = d ,其 等效 kernel size = k’
k’ = k + (k - 1) * (d - 1) ------------------------------(计算公式)
K’ = 3 + (3 - 1) * (2 - 1) = 5-------------------------------(图b的计算)
这里需要说明一下,经过膨胀处理后其卷积核数量不会变化,即原始为3×3,膨胀后还是3×3。为什么有一个等效,就是虽然膨胀后还是3×3,但是因其膨胀了,在计算感受野时其感受野是等效于一个5×5的卷积核。为了便于之后计算感受野,所以这里提出了等效卷积核。
2.2感受野计算

kernel size=3, stride=1 且 dilation rate 分别为 1, 2, 4 的三个不同的膨胀卷积


注:RF2对应的是图(a),RF3对应的图(b),RF4对应图(c)
计算RF2时,那个数字1为默认的原始图片感受野是1
图abc的整个计算过程如下:

四、膨胀卷积的问题
4.1 gridding effect
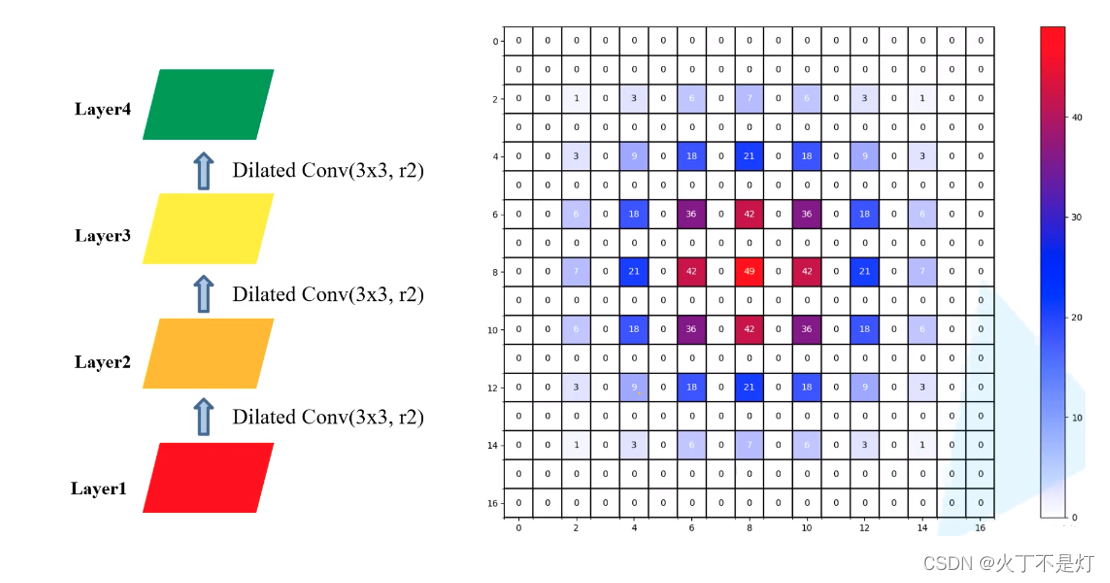
设定一个多层膨胀卷积如下图所示
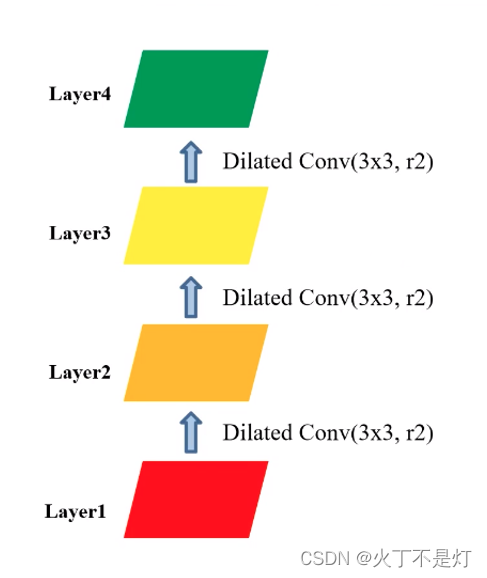
如下是每一层的过程:(从下往上看(从图4.4往图4.2看))

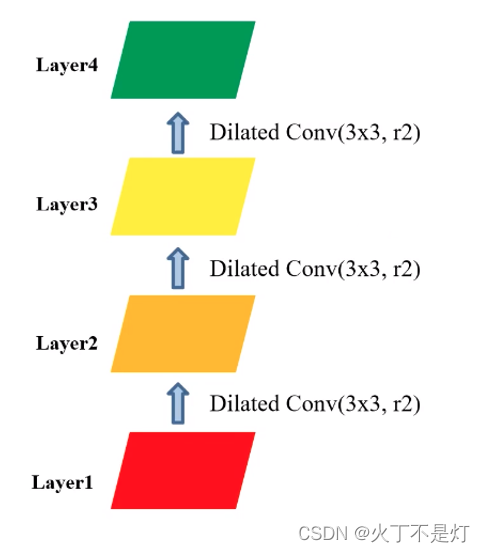
图4.2 layer4

图4.3 layer3

图4.4 layer2
#有数字的块(非0块)表示在经过膨胀卷积后使用到了这个像素块
#块里面的数字表示经过一系列的膨胀卷积之后该块的累计使用次数。(很好计算的,自己画一下就能知道)
经过三次膨胀卷积后得到了图4.2的右边,可以看出来,当多层膨胀卷积的膨胀率相同时(本例子均为2),在感受野内出现使用次数为0的像素块,即会出现使用的原始数据不连续从而导致信息的丢失。
4.2长距离的信息有时是不相关的
膨胀卷积扩大了感受野,因此可以取得长距离信息(在图像中这是有利于大目标分析的),但是有些长距离信息和当前点是完全不相关的,会影响数据的一致性(对于小目标不太友好)。
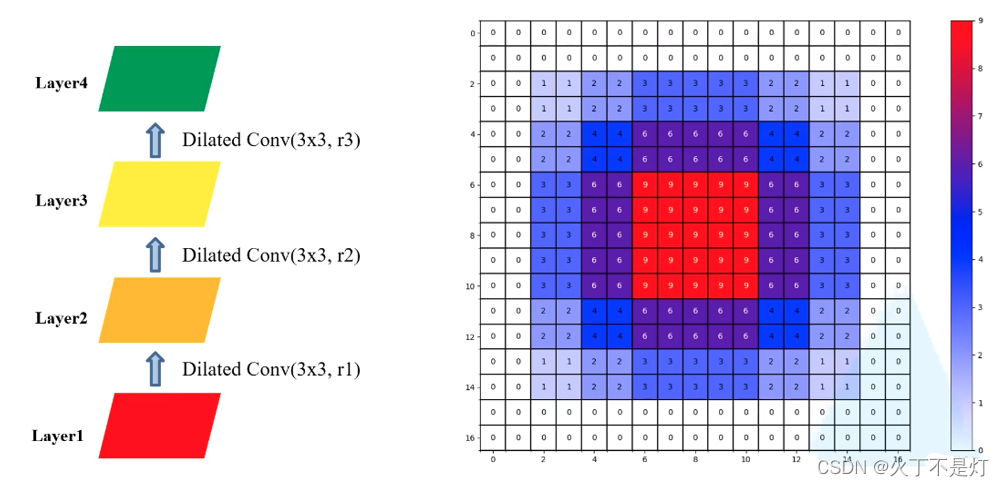
五、多层膨胀卷积设计规则HDC(解决四中的问题)
参考文章:Understanding Convolution for Semantic Segmentation
1.第二层的两个非零元素之间的最大距离小于等于该层卷积核的大小
2.将膨胀系数设置为锯齿形状。[1,2,3,1,2,3,1,2,3]
3.膨胀系数的公约数不能大于1。[2,4,8]不合理
HDC目标:经过一系列膨胀卷积后完全覆盖底层特征图,并且该区域没有任何孔洞或者缺失边缘
5.1理解第一条规则
第二层的两个非零元素之间的最大距离小于等于该层卷积核的大小

这个Mi怎么来的,在(63条消息) 语义分割--Understand Convolution for Semantic Segmentation_DFann的博客-CSDN博客
这一篇博客中,作者询问了Understanding Convolution for Semantic Segmentation文章的一作

对第一条规则举例①:

Mi是第i层两个非0元素之间的最大距离,ri是第i层的膨胀率
前面已经说明,对于最后一层,Mi = r i,所以计算时,M3 = r3 = 5 ,r2 = 2,得出1,其他同
M2 = 2,满足第二层的两个非零元素之间的最大距离小于等于该层卷积核的大小
对第一条规则举例②:

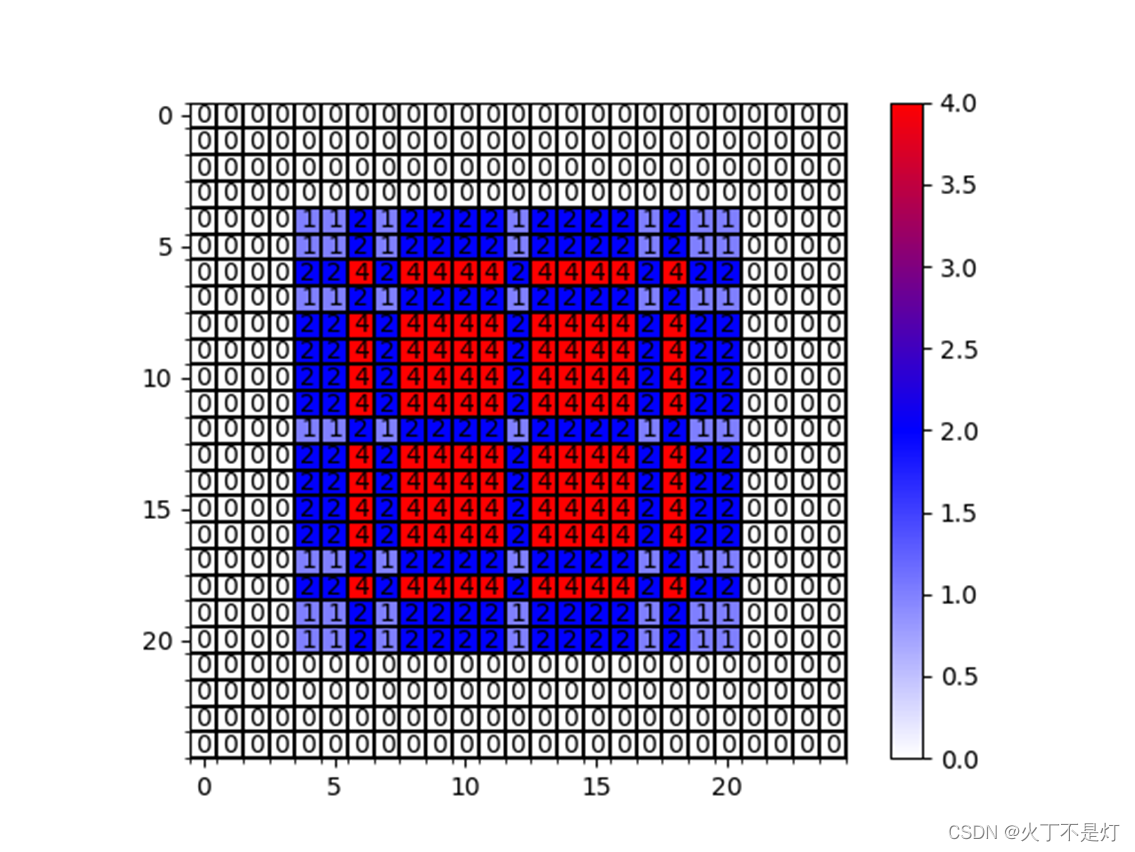

(卷积核均为3×3,左边膨胀率[1,2,5],右边膨胀率[1,2,9],跑出这个图的代码见附录)
通过规则1,还可以得出膨胀率必须从1开始的结论。
我们希望在高层特征图的每个像素可以利用到底层特征图的感受野内的所有像素,那么M应该等于1。M=1意味着非零元素之间是相邻的(没有间隙的),M等于1,所以r“被迫”为1
5.2理解第二条规则
将膨胀系数设置为锯齿形状(1,2,3,1,2,3)
在我们的网络中,膨胀率的分配遵循锯齿波状启发式:许多层被分组在一起,形成具有不断增加膨胀率的波的“上升边缘”,下一组重复相同的模式。例如,对于所有膨胀率r = 2的层,我们将3层作为一个组,并将它们的膨胀率分别改变为1、2和3。通过这样做,顶层可以从更广泛的像素范围内访问信息,它们位于与原始配置相同的区域内。这个过程在所有的层中都重复进行,从而使顶层的感受野保持不变。
---------Understanding Convolution for Semantic Segmentation原文翻译
5.3理解第三条规则
膨胀系数的公约数不能大于1
如果公约数大于1,仍然会出现gridding effect问题
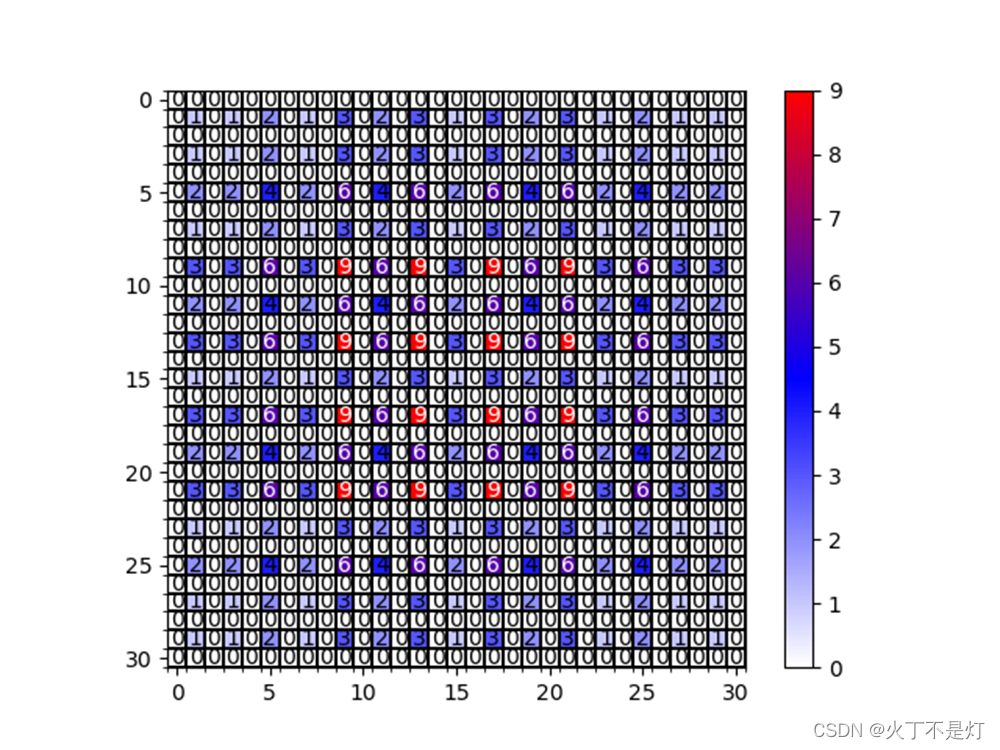
上图是膨胀率为[2,4,8],出现了gridding effect (代码见附录)
综上:多层膨胀卷积膨胀率的设计规范为
1.第二层的两个非零元素之间的最大距离小于等于该层卷积核的大小
2.将膨胀系数设置为锯齿形状。[1,2,3,1,2,3,1,2,3]
3.膨胀系数的公约数不能大于1。[2,4,8]不合理
5.4满足HDC原则的膨胀率设定及应用中的图片分割效果
(不满足HDC设计的膨胀率)
(满足HDC设计的膨胀率)
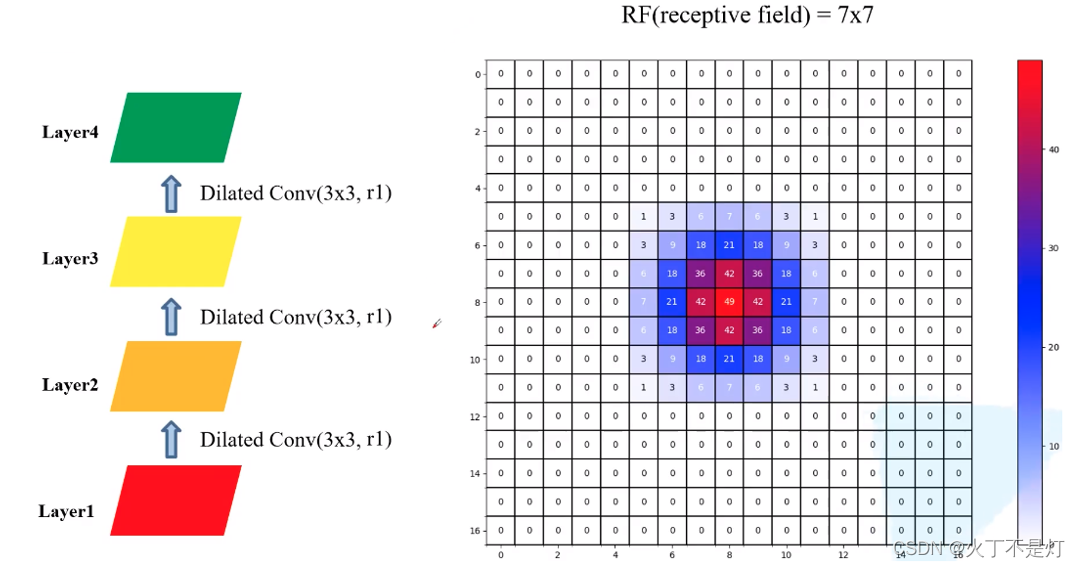
(普通标准多层卷积)
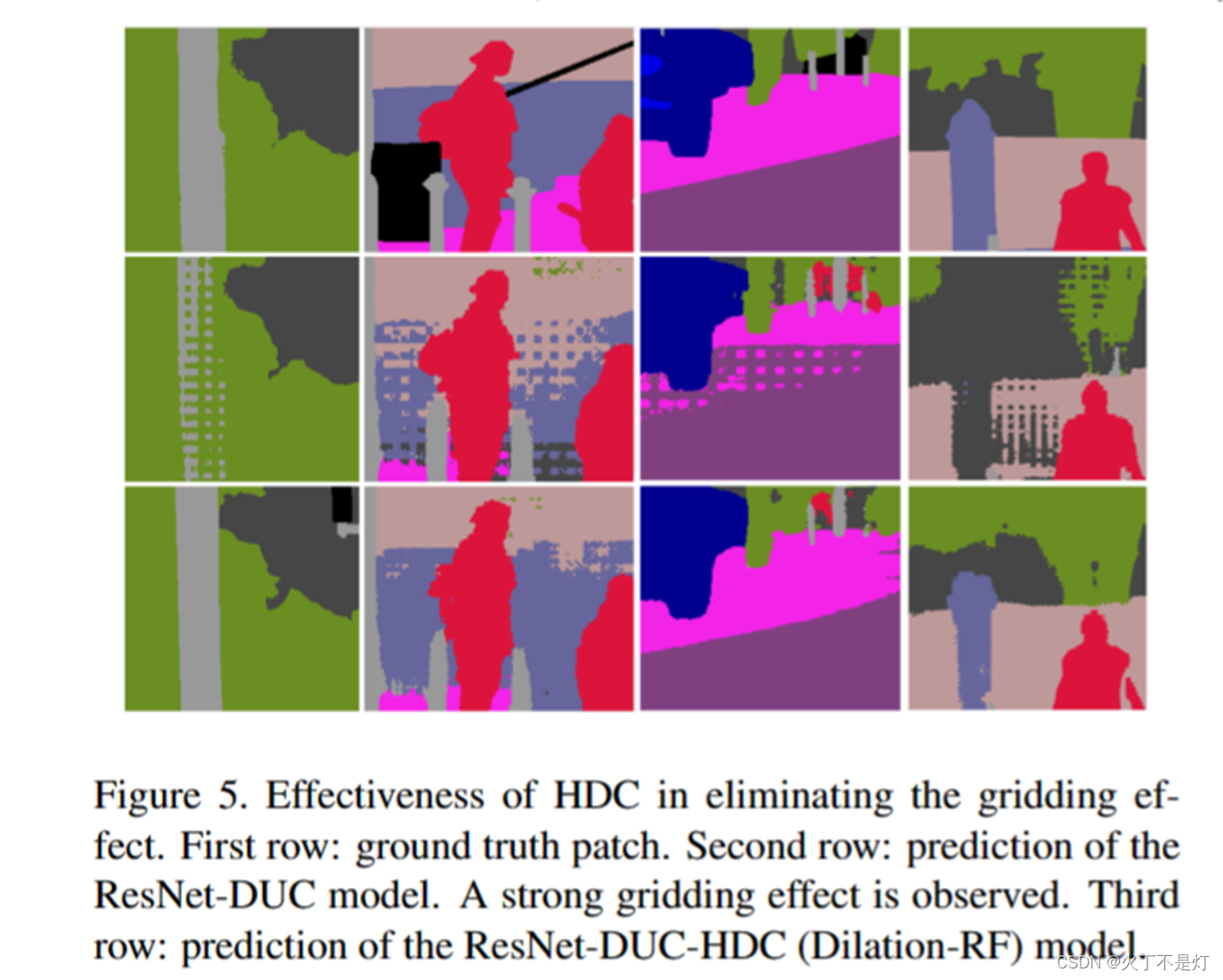 ( 满足和不满足HDC原则的图片分割效果)
( 满足和不满足HDC原则的图片分割效果)
附录1:膨胀卷积代码
一维膨胀卷积:
#一维膨胀卷积
conv1 = torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
二维膨胀卷积:
#二维膨胀卷积
conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=kernel_size, stride=stride, padding=padding, dilation=dilation, groups=groups, bias=bias)

当dilation = 1为一般卷积,dilation > 1为膨胀卷积
注意:膨胀卷积时的padding和膨胀率dilation取值有关系
一维时:
N是一个批处理大小,C表示多个通道, L 是信号序列的长度,若想输入和输出尺寸不变,则可以通过下式反解出padding

二维时:
o = output=**32**i = input **=32**p = padding=? **#未知量,需求**k = kernel_size=**3**s = stride=**1**d = dilation=**2**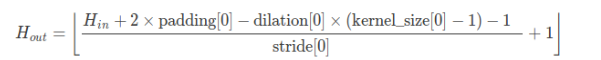
由上面的特征图计算公式,如果想保证输入和输出尺寸一致,利用上面公式反解出p
代入已知量得到方程式:
32=(32+2xpadding-2x(3-1)-1)/1+1
解方程得到:
padding=2
附录2:HDC绘制膨胀卷积代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
def dilated_conv_one_pixel(center: (int, int),
feature_map: np.ndarray,
k: int = 3,
r: int = 1,
v: int = 1):
"""
膨胀卷积核中心在指定坐标center处时,统计哪些像素被利用到,
并在利用到的像素位置处加上增量v
Args:
center: 膨胀卷积核中心的坐标
feature_map: 记录每个像素使用次数的特征图
k: 膨胀卷积核的kernel大小
r: 膨胀卷积的dilation rate
v: 使用次数增量
"""
assert divmod(3, 2)[1] == 1
left_top = (center[0] - ((k - 1) // 2) * r, center[1] - ((k - 1) // 2) * r)
for i in range(k):
for j in range(k):
feature_map[left_top[1] + i * r][left_top[0] + j * r] += v
def dilated_conv_all_map(dilated_map: np.ndarray,
k: int = 3,
r: int = 1):
"""
根据输出特征矩阵中哪些像素被使用以及使用次数,
配合膨胀卷积k和r计算输入特征矩阵哪些像素被使用以及使用次数
Args:
dilated_map: 记录输出特征矩阵中每个像素被使用次数的特征图
k: 膨胀卷积核的kernel大小
r: 膨胀卷积的dilation rate
"""
new_map = np.zeros_like(dilated_map)
for i in range(dilated_map.shape[0]):
for j in range(dilated_map.shape[1]):
if dilated_map[i][j] > 0:
dilated_conv_one_pixel((j, i), new_map, k=k, r=r, v=dilated_map[i][j])
return new_map
def plot_map(matrix: np.ndarray):
plt.figure()
c_list = ['white', 'blue', 'red']
new_cmp = LinearSegmentedColormap.from_list('chaos', c_list)
plt.imshow(matrix, cmap=new_cmp)
ax = plt.gca()
ax.set_xticks(np.arange(-0.5, matrix.shape[1], 1), minor=True)
ax.set_yticks(np.arange(-0.5, matrix.shape[0], 1), minor=True)
plt.colorbar()
thresh = 5
for x in range(matrix.shape[1]):
for y in range(matrix.shape[0]):
info = int(matrix[y, x])
ax.text(x, y, info,
verticalalignment='center',
horizontalalignment='center',
color="white" if info > thresh else "black")
ax.grid(which='minor', color='black', linestyle='-', linewidth=1.5)
plt.show()
plt.close()
def main():
dilated_rates = [2,4,8]
size = 30
m = np.zeros(shape=(size, size), dtype=np.int32)
center = size // 2
m[center][center] = 1
for index, dilated_r in enumerate(dilated_rates[::-1]):
new_map = dilated_conv_all_map(m, r=dilated_r)
m = new_map
print(m)
plot_map(m)
if __name__ == '__main__':
main()
版权归原作者 火丁不是灯 所有, 如有侵权,请联系我们删除。