温度参数大概是LLM推理中最容易理解的控制手段了。把温度调低,输出就更确定、更收敛;调高,模型就更发散、更有"创意"。问题是这套机制依赖于显式的logits——而连续自回归语言模型(CALM)恰恰没有这东西。
我们在前面CALM框架的介绍中看到,CALM基本上把架构都做过修改,但是唯独温度采样这块一直没动。
这时因为模型预测的是无限维空间中的连续向量,根本没法枚举所有可能输出,更别提计算概率了。 或者说我们只有一个能吐样本的黑盒,没有logits可以缩放,没有softmax可以操作。
调整token生成分布是语言模型最常用的技术之一操作也足够简单直接。
生产环境里几乎所有LLM部署都离不开温度采样——它决定了输出在创造性和确定性之间的平衡点
传统做法是在softmax之前对logits做缩放,直接重塑词汇表上的概率分布。但CALM的输出空间是连续的、无限的,这条路是走不通,那怎么办?本文要解决的就是这个问题:只靠抽样能力,不碰任何概率数值,照样可以实现温度控制。
这里介绍的技术补全了CALM工具链的最后一块拼图,证明连续语言模型在可控性上并不逊于传统token模型,效率优势还能保住
温度参数的工作原理
先快速回顾下经典温度采样的机制。设 x_i_ 为第 i 个token的logit,温度调整后的概率分布长这样: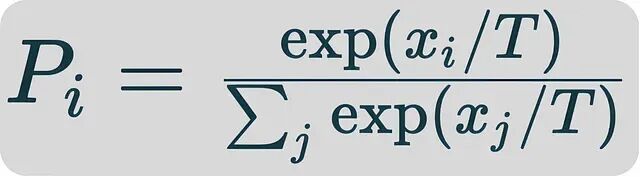
温度值 T 的作用很直观:T < 1* 时分布变尖锐,概率质量往头部token集中,适合编程、数学这类需要确定性的场景;*T > 1 时分布变平坦,尾部token也有更多机会被采到,适合创意写作、brainstorming。
本质上就是除以一个更大的 T 会压缩logit之间的差距,削弱softmax的"赢家通吃"效应,但CALM每一步并不输出有限词汇表上的离散分布,自然也就没有logits向量可供缩放
这就是为什么需要一套完全不依赖似然函数的替代方案。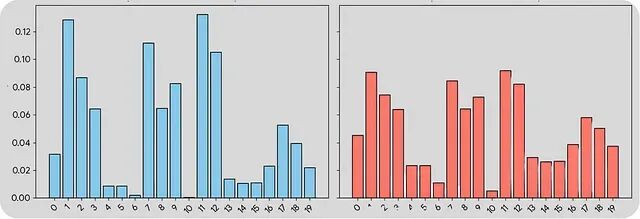
上图展示了温度对分布形状的影响:左边低温,分布尖锐、确定性强;右边高温,分布平坦、多样性高。
只有样本,没有概率?照样能做温度控制
CALM的生成器就是个黑盒:可以从里面抽样本,但拿不到概率值也没有logits。
一个看不见的分布,怎么让它变尖或变平?
核心思路和经典温度采样相同的目标,从温度调整后的分布中采样但把直接操作概率的步骤全部换成纯采样操作。具体来说,假设有个基础采样器能产生 *x∼P(x)*,目标是构造一个新采样器产生 *x∼PT(x)*,且只能用原采样器反复抽样这一种手段。
下一步是把温度采样重写成不需要logits的形式,这就是后续所有推导的"起点公式":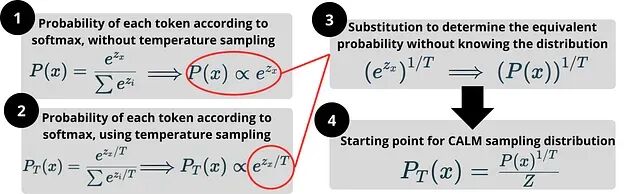
有了这个公式就能在连续生成模态下复刻温度采样的效果。
碰撞方法(collision method) 提供了基础框架。但是还有一个重要的问题:1/T 不是整数怎么办?
碰撞技巧的基本原理
先把CALM的采样适配到温度控制框架上。这里需要用到碰撞方法:抽取多个独立样本,根据它们的匹配情况来间接确定概率。
这里说的"样本x"是单个CALM解码步骤产生的整个K-token块,不是单个token
当 T =1/ n(n为正整数)时,温度调整后的分布正比于 P ( x ) ⁿ
碰撞技巧的数学基础是独立性:n次独立抽样全部等于同一个块x的概率恰好是 P ( x ) n
操作方法就是抽n个样本,全部相同才接受否则拒绝重来
举个例子:某个块的概率是 P (__ x __)=0.2,那三路碰撞的概率就是 0.2 ³ =0.008
问题在于 1/ T 一般不是整数,比如没法抽"3.33个样本"。而且低温度情况下拒绝率会很高,比如 T =0.1 意味着需要连续10个完全相同的样本,所以整数部分和小数部分必须分开处理,这就引出了分解策略。
指数分解:拆成整数和小数两部分
分解策略把指数运算的代数规则映射到概率上,把 1/T 拆成整数 n 和小数 α 两个分量: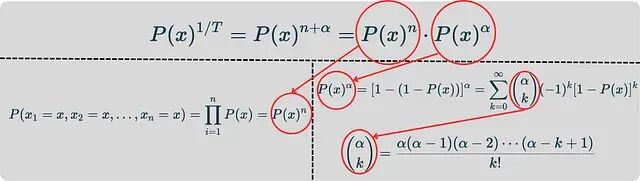
整数部分用碰撞方法搞定,小数部分得靠伯努利工厂配合广义二项级数。
比如 T=0.3,那 1/T=3.33,于是 n=3,α=0.33
整数分量处理起来相对简单,还是碰撞方法那套。
小数分量就麻烦了,没法用样本重复的方法,所以要把问题转化成无限级数形式。这就是伯努利工厂的用武之地:用只能访问概率为 p 的硬币,"制造"出一个概率为 p ᵅ 的有偏硬币。
所谓"概率为p的硬币"其实就是个匹配指示器:从基础采样器抽一个样本,跟目标x相等就返回成功。这是个伯努利随机变量(真/假),成功概率等于 p=P(x)
两部分必须同时满足,采样才算有效。
数学上这套东西还是很好解释的但计算上有个严重瓶颈。低温度的情况下——比如 T=0.1——需要连续10个相同样本。模型可能要跑几百万次才出一个有效结果。
批量近似:让低温采样变得可行
作者给出的解法是批量近似。与其等连续n个相同样本,不如一次性抽一大批样本(N >> n)然后在里面找重复。
具体操作如下:假设 n=10(即 T=0.1),一次抽 N=200 个样本统计每个块出现的次数,出现次数≥10的块就成为整数部分阶段的合格候选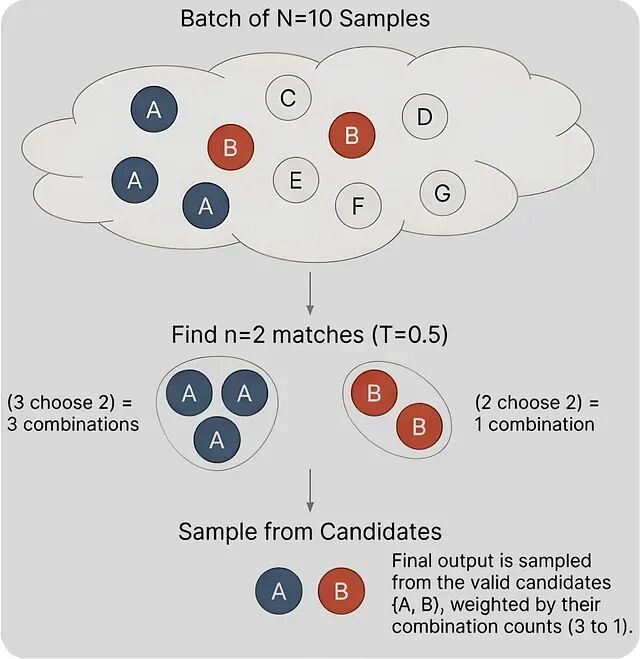
当 N=10、n=2 时,合格候选就是那些在10个样本里出现至少2次的块,这可比等连续相同样本高效多了。
这种做法用一次可并行的批量抽样替代了反复重启,低温情况下的样本利用率大幅提升。
结合组合数学,低温和小数分量的问题都有了稳健解法。温度被正确迁移到隐式分布上,创造性和精确性之间的调节照样能做,而且根本不需要知道真实分布长什么样。
这对CALM意味着什么
这套采样框架补齐了CALM工具链,剩下的挑战主要是工程层面的:让低温解码在实际推理中跑得够快。批量近似提供了思路——不用反复重启等碰撞,抽一个大批次然后在里面找,熟悉的创造性↔精确性旋钮就保住了。
这个思路的适用范围远不止CALM。任何能采样但没法给概率打分(或做归一化)的隐式生成模型都能复用同样的原理。
扩散语言模型、流匹配架构同样适用
另外值得一提的是CALM把自回归步数降到了原来的 1/K(比如 K=4 时就是4倍压缩),而上面这套采样框架保住了细粒度的解码控制,而实用性没打折扣。
技术贡献总结
核心创新点在于:不需要概率值也能做温度控制。方法是把概率重加权 P(x)ⁿ 转化成一个采样事件——只在n个独立抽样碰撞到同一结果时接受。
数学上的关键技巧是把 1/T 写成 n + α 的形式。整数指数靠碰撞解决,小数指数靠伯努利工厂搞定 p ᵅ。
工程上的突破是批量近似:一次并行批量加组合分组,取代了低效的反复重启,低温解码终于变得可行。
更广泛地看,这套方法适用于所有"能采样但没法评分归一化概率"的隐式模型——扩散模型、流匹配等新范式都能用。
作者:Fabio Yáñez Romero