机器学习和深度学习概述

学习笔记根据百度飞浆课程学习

人工智能、机器学习、深度学习的关系

人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的，三者的关系如下图所示，即：人工智能 > 机器学习 > 深度学习。

人工智能（ArtificialIntelligence，AI）是最宽泛的概念，是研发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。由于这个定义只阐述了目标，而没有限定方法，因此实现人工智能存在的诸多方法和分支，导致其变成一个“大杂烩”式的学科。

机器学习（MachineLearning，ML）是当前比较有效的一种实现人工智能的方式。

深度学习（DeepLearning，DL）是机器学习算法中最热门的一个分支，近些年取得了显著的进展，并替代了大多数传统机器学习算法。

机器学习

• 机器学习是什么 —— 无序数据转化为价值
• 机器学习价值 —— 从数据中抽取规律，并用来预测未来（比如：淘宝可以根据你的浏览痕迹向你推荐商品，这就是一个典型的机器学习产生价值的例子）
• 机器学习应用举例 > 1. 分类问题:：图像识别、垃圾邮件识别、世界杯中摄像头选择的切换画面> 2. 回归问题：股价预测、房价预测> 3. 排序问题：点击率预估、推荐> 4. 生成问题：图像生成、图像风格转换、图像文字描述生成
• 机器学习应用流程
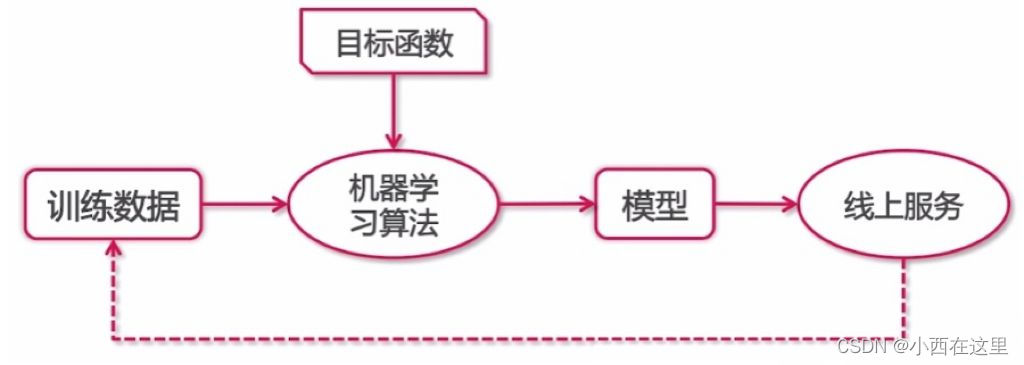
• 职责 > 1. 数据处理（数据采集 + 数据去噪）> 2. 模型训练（提取特征 + 训练模型）> 3. 模型评估和优化（MSE、F1-score、AUC+调参）> 4. 模型应用（A/B 测试）

机器学习的实现

机器学习的实现可以分成两步：训练和预测，类似于归纳和演绎：

• 归纳： 从具体案例中抽象一般规律，机器学习中的“训练”亦是如此。从一定数量的样本（已知模型输入X和模型输出Y）中，学习输出Y与输入X的关系（可以想象成是某种表达式）。
• 演绎： 从一般规律推导出具体案例的结果，机器学习中的“预测”亦是如此。基于训练得到的Y与X之间的关系，如出现新的输入X，计算出输出Y。通常情况下，如果通过模型计算的输出和真实场景的输出一致，则说明模型是有效的。

“机器思考”的过程中确定模型的三个关键要素：假设、评价、优化

模型有效的基本条件是能够拟合已知的样本

损失函数（损失Loss）：衡量模型预测值和真实值差距的评价函数

如何确定模型参数？

图3 是以H为模型的假设，它是一个关于参数w和输入x的函数，用H(w,x) 表示。模型的优化目标是H(w,x)的输出与真实输出Y尽量一致，两者的相差程度即是模型效果的评价函数（相差越小越好）。那么，确定参数的过程就是在已知的样本上，不断减小该评价函数（H和Y的差距）的过程。直到模型学习到一个参数w，使得评价函数的值最小，衡量模型预测值和真实值差距的评价函数也被称为损失函数（损失Loss）。

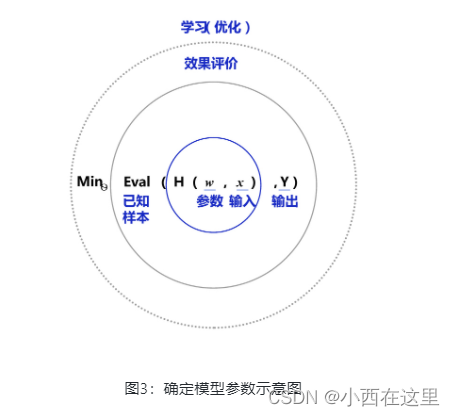
假设机器通过尝试答对（最小化损失）大量的习题（已知样本）来学习知识（模型参数w），并期望用学习到的知识所代表的模型H(w,x)，回答不知道答案的考试题（未知样本）。最小化损失是模型的优化目标，实现损失最小化的方法称为优化算法，也称为寻解算法（找到使得损失函数最小的参数解）。参数w和输入x组成公式的基本结构称为假设。在牛顿第二定律的案例中，基于对数据的观测，我们提出了线性假设，即作用力和加速度是线性关系，用线性方程表示。由此可见，模型假设、评价函数（损失/优化目标）和优化算法是构成模型的三个关键要素。

模型结构

模型假设、评价函数和优化算法是如何支撑机器学习流程的呢？如图4 所示。

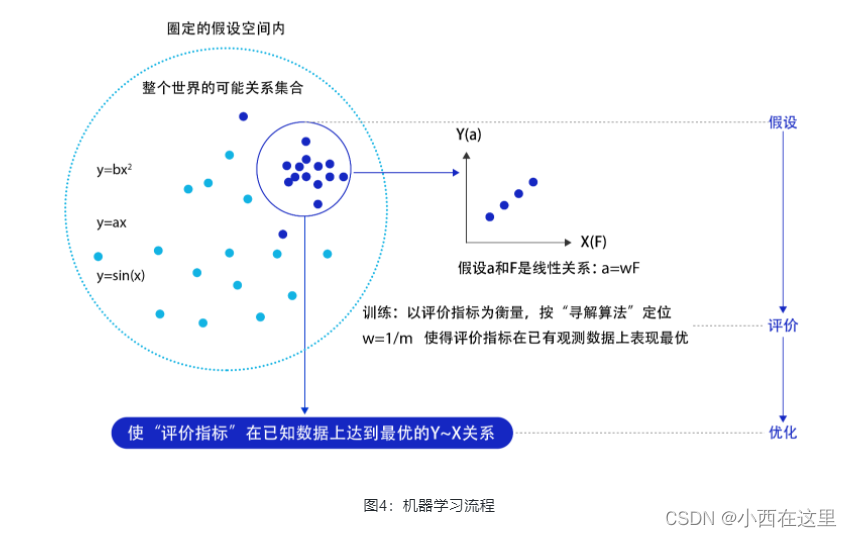
• 模型假设：世界上的可能关系千千万，漫无目标的试探YX之间的关系显然是十分低效的。因此假设空间先圈定了一个模型能够表达的关系可能，如蓝色圆圈所示。机器还会进一步在假设圈定的圆圈内寻找最优的YX关系，即确定参数w。
• 评价函数：寻找最优之前，我们需要先定义什么是最优，即评价一个Y~X关系的好坏的指标。通常衡量该关系是否能很好的拟合现有观测样本，将拟合的误差最小作为优化目标。
• 优化算法：设置了评价指标后，就可以在假设圈定的范围内，将使得评价指标最优（损失函数最小/最拟合已有观测样本）的Y~X关系找出来，这个寻找最优解的方法即为优化算法。最笨的优化算法即按照参数的可能，穷举每一个可能取值来计算损失函数，保留使得损失函数最小的参数作为最终结果。

机器执行学习任务的框架体现了其学习的本质是“参数估计”（Learning is parameter estimation）。

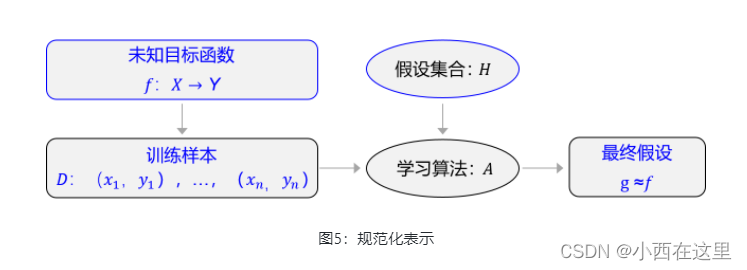
上述方法论使用更规范化的表示如图5所示，未知目标函数f，以训练样本D=（x1，y1），…，（xn，yn）为依据。从假设集合H中，通过学习算法A找到一个函数g。如果g能够最大程度的拟合训练样本D，那么可以认为函数g就接近于目标函数f。

深度学习

相比传统的机器学习算法，深度学习做出了哪些改进呢？其实两者在理论结构上是一致的，即：模型假设、评价函数和优化算法，其根本差别在于假设的复杂度。

神经网络的基本概念

人工神经网络包括多个神经网络层，如：卷积层、全连接层、LSTM等，每一层又包括很多神经元，超过三层的非线性神经网络都可以被称为深度神经网络。通俗的讲，深度学习的模型可以视为是输入到输出的映射函数，足够深的神经网络理论上可以拟合任何复杂的函数。因此神经网络非常适合学习样本数据的内在规律和表示层次，对文字、图像和语音任务有很好的适用性。这几个领域的任务是人工智能的基础模块，因此深度学习被称为实现人工智能的基础也就不足为奇了。

神经网络基本结构如 图9 所示。

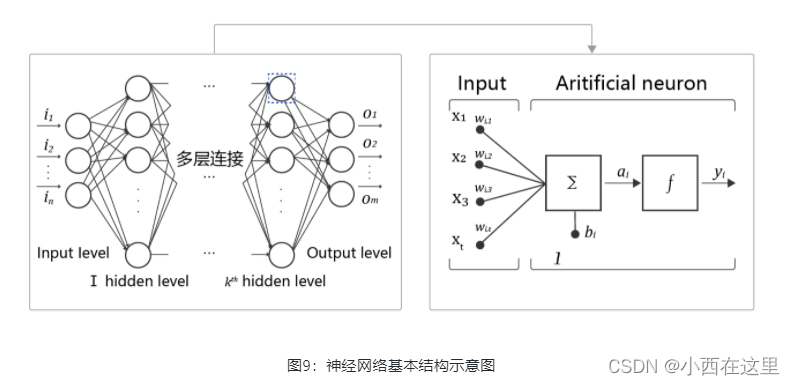
• 神经元： 神经网络中每个节点称为神经元，由两部分组成： - 加权和：将所有输入加权求和。- 非线性变换（激活函数）：加权和的结果经过一个非线性函数变换，让神经元计算具备非线性的能力。
• 多层连接： 大量这样的节点按照不同的层次排布，形成多层的结构连接起来，即称为神经网络。
• 前向计算： 从输入计算输出的过程，顺序从网络前至后。
• 计算图： 以图形化的方式展现神经网络的计算逻辑又称为计算图，也可以将神经网络的计算图以公式的方式表达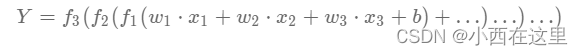： 神经网络的本质是一个含有很多参数的“大公式”

** 实现了端到端的学习**

在数据充足的情况下，深度学习模型可以实现端到端的学习，即不需要专门做特征工程，将原始的特征输入模型中，模型可同时完成特征提取和分类任务，如 图14 所示。

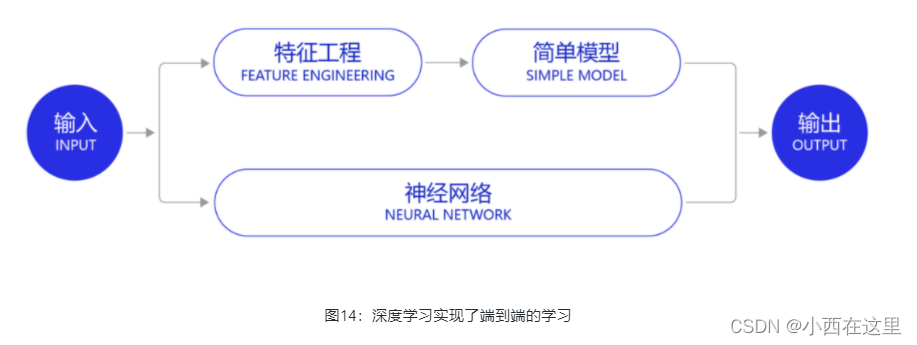
以计算机视觉任务为例，特征工程是诸多图像科学家基于人类对视觉理论的理解，设计出来的一系列提取特征的计算步骤，典型如SIFT特征。在2010年之前的计算机视觉领域，人们普遍使用SIFT一类特征+SVM一类的简单浅层模型完成建模任务。

说明：

SIFT特征由David Lowe在1999年提出，在2004年加以完善。SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT特征的信息量大，适合在海量数据库中快速准确匹配。

** 实现了深度学习框架标准化**

除了应用广泛的特点外，深度学习还推动人工智能进入工业大生产阶段，算法的通用性导致标准化、自动化和模块化的框架产生，如 图15 所示。

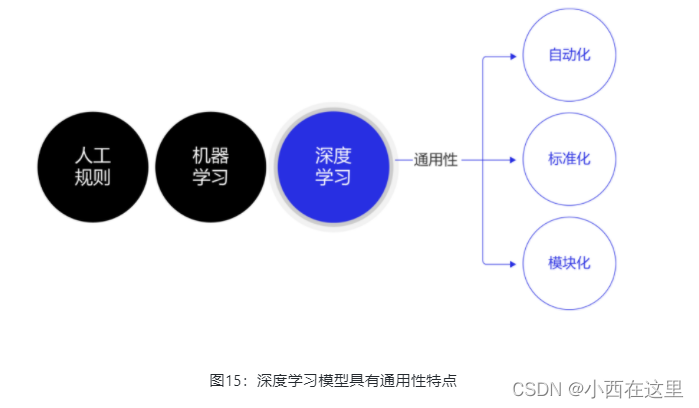
在此之前，不同流派的机器学习算法理论和实现均不同，导致每个算法均要独立实现，如随机森林和支撑向量机（SVM）。但在深度学习框架下，不同模型的算法结构有较大的通用性，如常用于计算机视觉的卷积神经网络模型（CNN）和常用于自然语言处理的长期短期记忆模型(LSTM)，都可以分为组网模块、梯度下降的优化模块和预测模块等。这使得抽象出统一的框架成为了可能，并大大降低了编写建模代码的成本。一些相对通用的模块，如网络基础算子的实现、各种优化算法等都可以由框架实现。建模者只需要关注数据处理，配置组网的方式，以及用少量代码串起训练和预测的流程即可。

教程链接：飞桨PaddlePaddle-源于产业实践的开源深度学习平台