【统计模型】大学生恋爱数据分析报告

大学生恋爱数据分析报告

    内容提要：本文依据“大学生恋爱数据”，对大学生恋爱状况和恋爱影响因素进行分析。被调查的学生中，大四学生最多，男女比例基本一致，大部分学生来自于二三线城市，身高介于155-185cm之间，体重介于40-70kg之间。被调查学生中，72%的人恋爱，大部分人被别人追求过且为党员，且会跑步、打羽毛球、吹乐器和唱歌。用全模型对第一个受访者的恋爱状况进行预测时，分界点*α=0.5*时判断正确，*α=0.3*时判断错误。是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱和每月话费对是否恋爱由显著影响。结合ROC曲线和AUC值可以得出，三个模型中AIC模型分类效果最好。

一、研究目的

  近年来，老龄化愈发严重，新生儿出生率显著降低。婚姻是生育的前提，探究现代人的婚恋观具有重要意义。00后婚恋观与以往发生了较大变化，计划终生不婚在00后中较为常见，调研青年人婚恋观的影响因素，对于提升生育率有重要意义。本文旨在依据“大学生恋爱数据”，分析大学生恋爱现状，进而得出大学生恋爱的影响因素。

二、数据来源和相关说明

  数据来源于“大学生恋爱数据”文件，据此分析大学生恋爱现状与影响因素。数据共包含32个变量，包括一个因变量和31个自变量。根据变量的含义，将31个变量分为了七类——基本信息、恋爱情况、职务情况、运动情况、才艺情况、颜值情况和生活规划情况。由于变量较多，本文用给定的符号代表这些变量，具体符号与变量解释如表2-1所示。

表2-1 变量解释与符号

变量

解释

符号

变量

解释

符号

是否恋爱

0-否;1-是

Y

唱歌

0-否;1-是

CY1

年级

1-大一;2-大二;

3-大三;4-大四

JB1

主持

0-否;1-是

CY2

性别

0-男;1-女

JB2

舞蹈

0-否;1-是

CY3

家乡

1-一线城市;2-二线城市;

3-三线城市;4-县级市;

5-农村

JB3

乐器

0-否;1-是

CY4

身高

连续变量

JB4

其他才艺

0-否;1-是

CY5

体重

连续变量

JB5

是否戴眼镜

0-否;1-是

YZ1

是否追求过别人

0-否;1-是

LA1

颜值

连续变量

YZ2

是否被别人追求过

0-否;1-是

LA2

每周自习时间

连续变量

GH1

寝室同学是否谈过恋爱

0-否;1-是

LA3

每周娱乐时间

连续变量

GH2

班干部

0-否;1-是

ZW1

每周睡觉时间

连续变量

GH3

党员

0-否;1-是

ZW2

每周运动时间

连续变量

GH4

足球

0-否;1-是

YD1

每月话费

连续变量

GH5

篮球

0-否;1-是

YD2

学生组织个数

连续变量

GH6

乒乓球

0-否;1-是

YD3

成绩水平

连续变量

GH7

羽毛球

0-否;1-是

YD4

生活费_百元

连续变量

GH8

跑步

0-否;1-是

YD5

台球

0-否;1-是

YD6

三、描述性统计分析

  为了获得对数据的整体了解，本文先对数据进行了描述性统计分析。考虑到变量较多，本文从基本情况、恋爱情况、职务情况、运动情况、才艺情况、颜值情况、生活规划情况和变量间的相关性八个方面对数据进行可视化。

3.1 基本情况

  为了分析学生基本情况，本文绘制了饼图和直方图，分别如图3-1和3-2所示。

（1）年级、性别、家乡情况

图3-1 学生基本情况饼图

  由图3-1可以得出：

• 被调查的学生中，大一到大三年级人数较少，占比在14%~20%之间内，大四人数最多，约占到被调查学生的一半，占比48.8%。
• 男生占比49.1%，女生占比50.9%，男女比例基本符合1：1。
• 家乡来源中，二线城市人数最多，占比38.6%，其次为三线城市和县级市，分别占比28%和14.3%，农村人数最少，仅占比7.5%。

（2）身高、体重情况

图3-2 学生身高、体重直方图

  由图3-2可以得出：

• 学生身高在165cm-170cm频数最高，大部分学生的身高集中在155cm-185cm范围内，学生的身高状况大致服从正态分布。
• 学生体重在50kg-60kg频数最高，大部分学生的体重集中在40kg-70kg范围内，学生的体重状况也大致服从正态分布。

3.2 恋爱情况

（1）恋爱比例

图3-3 是否恋爱饼图

  由图3-3可以得出：被调查的大学生中，72%的学生在恋爱，只有28%的学生未恋爱，即大学生恋爱比例还是相对较高的。

（2）恋爱史

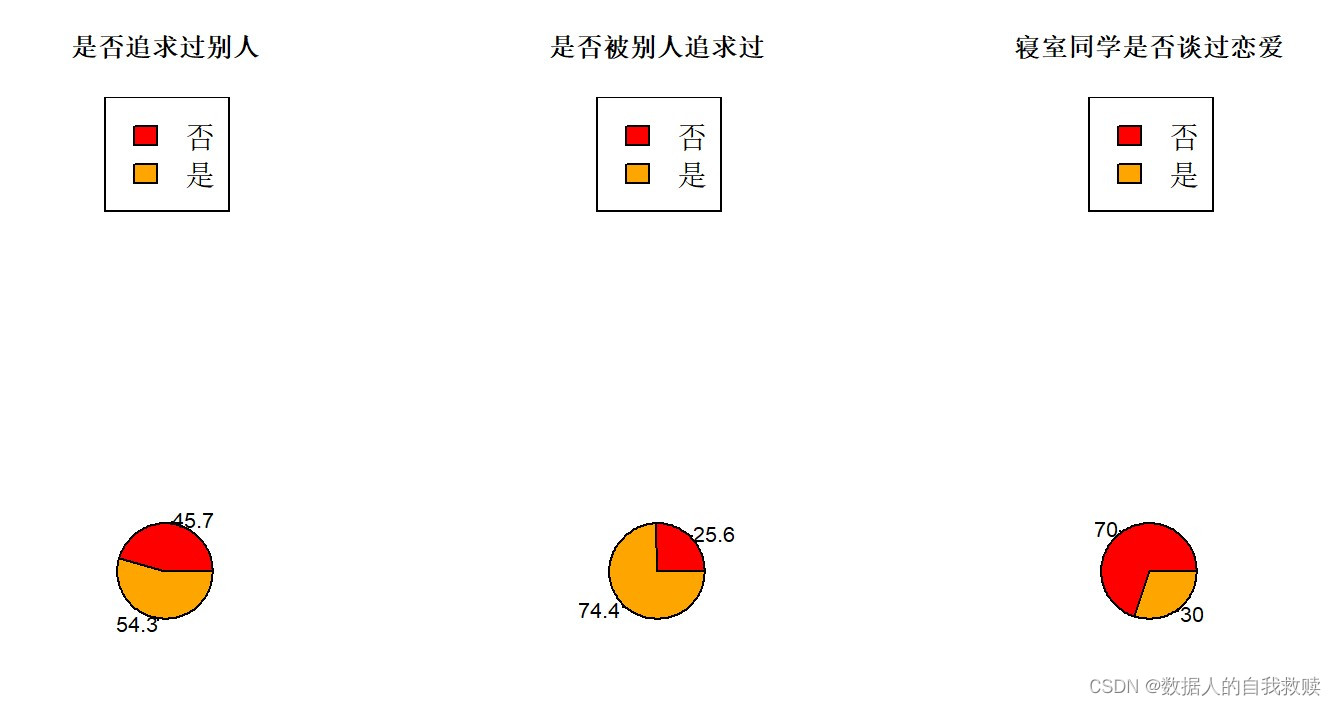
图3-4 学生恋爱史饼图

  由图3-4可以得出：

• 有54.3%的学生追求过别人，45.7%的学生没有追求过别人，追求过别人的人占总人数的一半以上。
• 有74.7%的学生被别人追求过，25.6%的学生没有被别人追求过，较大部分学生被别人追求过。
• 有70%的同学寝室同学没有谈过恋爱，有30%的同学寝室同学没有谈过恋爱，寝室同学谈过恋爱的同学占比较少。

3.3 职务担任情况

图3-5 职务担任情况饼图

  由图3-5可以得出：学生中65.6%是班干部，81.6%是党员，班干部学生占比一半以上，学生证大部分都是党员。

3.4 运动情况

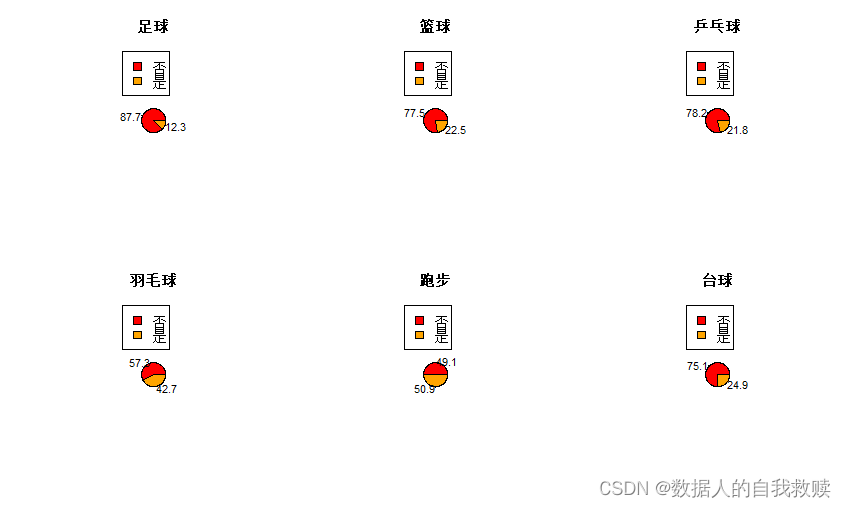
图3-6 学生运动情况饼图

  由图3-6可以得出：跑步、羽毛球和台球比较受被调查大学生的欢迎，分别占比50.9%、42.7和24.9；足球最不受被调查大学生的欢迎，占比仅为12.3%。

3.5 才艺情况

图3-7 学生才艺情况饼图

  由图3-7可以得出：学生中会其他才艺、乐器和唱歌的人数较多，分别占比54.6%、37.9%和33.4%，学生中会主持和舞蹈的人数较少，仅占比8%~9%。

3.6 颜值情况

图3-8 学生颜值状况

  由图3-8可以得出：69.3%的学生均佩戴眼镜，占总人数的一半以上；学生的颜值在4-5分之间人数最多，远远多于其他组颜值；相较于低颜值，高颜值人群人数要多于低颜值人群，即人群整体颜值集中在4-10分，极低颜值人数较少。

3.7 生活规划情况

图3-9 学生生活规划情况

  由图3-9可以得出：学生每周自习时间集中在0-20h，其中5-10h与15-20h人数最多；学生每周娱乐时间集中在0-30和，其中0-10h人数最多；学生每周睡觉时间集中在40-60h，其中50-60h人数最多；学生每周运动时间集中在0-10h，其中0-5h人数最多；学生每月话费集中在30-60元和90-100元，其中90-100元人数最多；学生组织个数集中在0.5-1、1.5-2和2.5-3，其中2.5-3人数最多；学生成绩水平分布较为均匀，其中40-50分人数最多；学生生活费集中在0-3000元，其中1000-2000元人数最多。

3.8 变量间的相关性

（1）连续型变量热力图

图3-10 相关性热力图

  由图3-10可以得出：除了身高和体重间的相关性外，其他各个变量间的相关性非常弱。身高和体重的相关系数为0.75，属于中强度正相关关系，其他变量间的相关系数绝对值均不超过0.25，因而相关关系非常弱。

（2）连续变量与是否恋爱的关系

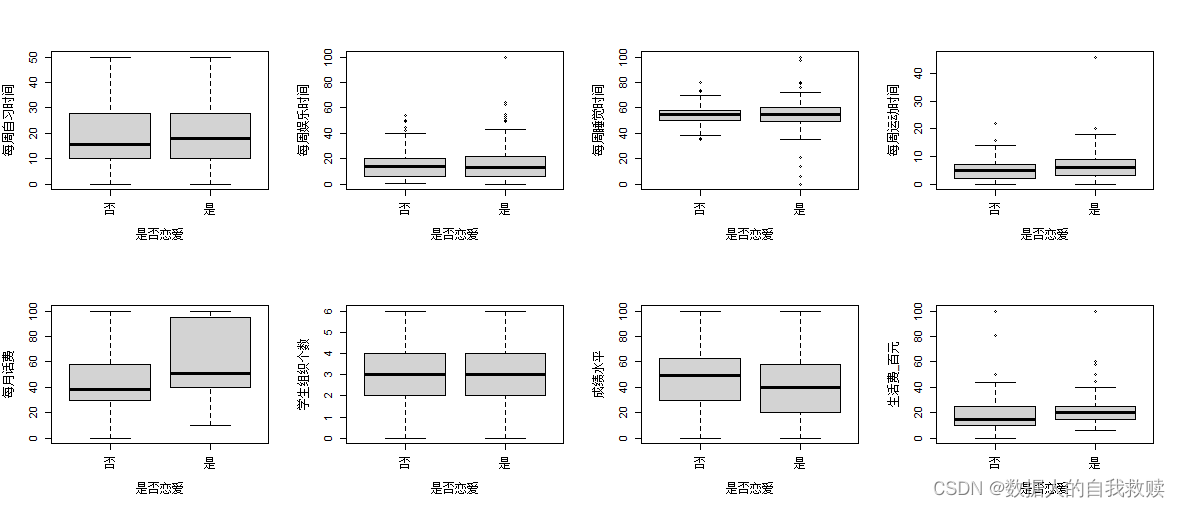
图3-11 箱线图

    由图3-11可以得出：生活规划的变量在是否恋爱上不全存在差异性，从箱线图可以看出，每月话费、成绩水平和生活费在是否恋爱上存在较大的差异性，其它的变量差异性较小或几乎不存在差异性。

四、数据建模

4.1 全模型

（1）模型建立

  将所有变量全部纳入模型，建立logistic回归模型，模型形式如下：

logit*p=*ln(*p/1p)=β0**+β1as.factorJB12+β2as.factorJB13+β3as.factorJB14+β4JB2+β5as.factorJB32+β6as.factorJB33+β7as.factorJB34+β8as.factorJB35+β9JB4*+*β10JB5+β11LA1+β12LA2+β13LA3+β14ZW1+β15ZW2+β16YD1+β17YD2+β18YD3+β19YD4+β20YD5+β21YD6+β22CY1+β23CY2+β24CY3+β25CY4+β26CY5+β27YZ1+β28YZ2+β29GH1+β30GH2+β31GH3+β32GH4+β33GH5+β34GH6+β35GH7+β36*GH8

    模型的参数估计如表4-1所示。

表4-1 全模型参数估计

变量

Estimate

Pr(>|z|)

变量

Estimate

Pr(>|z|)

(Intercept)

-4.4842

0.4128

YD4

-0.3917

0.3192

as.factor(JB1)2

-0.5786

0.3699

YD5

0.1803

0.6461

as.factor(JB1)3

0.2452

0.7283

YD6

1.1374

0.01987*

as.factor(JB1)4

-0.0625

0.9178

CY1

0.1752

0.6890

JB2

0.3651

0.5629

CY2

1.1006

0.1791

as.factor(JB3)2

0.0259

0.9702

CY3

-0.7648

0.2619

as.factor(JB3)3

-0.5337

0.4534

CY4

0.4320

0.3584

as.factor(JB3)4

-0.2499

0.7645

CY5

0.7619

0.1108

as.factor(JB3)5

-1.2400

0.1846

YZ1

0.2786

0.4953

JB4

0.0056

0.8628

YZ2

0.1027

0.2201

JB5

-0.0015

0.9501

GH1

0.0033

0.8182

LA1

2.0757

2.74e-06***

GH2

0.0085

0.6225

LA2

2.1950

1.76e-07***

GH3

0.0070

0.7362

LA3

1.5127

0.00234**

GH4

0.0017

0.9685

ZW1

-0.5238

0.2207

GH5

0.0136

0.08147·

ZW2

-0.0978

0.8492

GH6

0.1609

0.1713

YD1

-0.3616

0.5976

GH7

-0.0122

0.1121

YD2

-0.0400

0.9415

GH8

-0.0066

0.4049

YD3

-0.9684

0.03585*

    由表4-1可以得出：

• 并不是所有的变量都在统计学意义上显著，其中变量LA1、LA2、LA3、YD3和YD6在统计学意义上显著，即变量是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱、乒乓球、台球在统计学意义上显著，其他自变量不显著。
• 追求过别人，学生恋爱的优势变为原来的7.97倍；被别人追求过，学生恋爱的优势变为原来的8.98倍；寝室同学谈过恋爱，学生恋爱的优势变为原来的4.54倍；打乒乓球，学生恋爱的优势变为原来的0.38倍，即学生恋爱发生的可能性降低；打台球，学生恋爱的优势变为原来的3.12倍。这些变化都在统计学意义上显著。
• 与大一学生相比，大二和大四学生恋爱的优势是大一学生的0.56倍和0.94倍，大三学生恋爱的优势是大一学生的1.28倍，即四个年级中，大三学生更可能谈恋爱，其次是大一学生、大四学生，最不可能谈恋爱的是大二学生，这些在统计学上不具有显著性。
• 与男学生相比，女学生恋爱的有时比是男同学的1.44倍，但这在统计学上不具有显著性。
• 与一线城市相比，二线城市学生恋爱的优势是其1.03倍，三线城市、县级市和农村学生恋爱的优势是其0.59倍、0.78倍和0.29倍，即二线城市学生最容易恋爱，其次是一线城市、县级市和三线城市，最后是农村学生。但是这些在统计学上不显著。
• 在其他条件不变的条件下，身高每增加1cm，学生恋爱的优势变为未增加时的1.0056倍；体重每增加1kg，学生恋爱的优势变为未增加前的0.99倍。但这些在统计学上不显著。
• 班干部、党员、踢足球、篮球、打羽毛球的学生恋爱的优势要低于非这些的学生，但是在统计学上不显著。
• 跑步、会唱歌、主持、乐器和其他才艺的学生恋爱的优势要高于非这些的学生，但在统计学上不显著。
• 学生的生活规划变量均对学生恋爱的优势比有正向影响，但这些影响在统计学上不存在显著性。

（2）结果预测

    用全模型对第一个受访者的恋爱概率进行预测，预测值为-0.46617305，则恋爱的概率为*p(Y=1)* = 0.385522。当分界点*α=0.5*时，第一个受访者被判为不恋爱，当分界点*α=0.3*时，第一个受访者被判为恋爱。第一个受访者本身是不恋爱，因而*α=0.5*时判断正确，*α=0.3*时判断错误。

4.2 基于AIC准则下的选模型A

  基于AIC准则对全模型的变量进行选择，得到选模型A，模型参数估计值如表4-2所示。

表4-2 选模型A参数估计结果

变量

Estimate

Std.Error

z value

Pr(>|z|)

(Intercept)

-1.9104

0.5541

-3.4480

0.0006***

LA1

1.8057

0.3593

5.0250

5.03e-07***

LA2

2.1443

0.3574

5.9990

1.98e-09***

LA3

1.2134

0.4250

2.8550

0.0043*

YD3

-0.8502

0.4013

-2.1190

0.0341*

YD6

0.9293

0.4378

2.1230

0.0338*

GH5

0.0139

0.0062

2.2380

0.0252*

GH7

-0.0098

0.0063

-1.5590

0.1189

  由表4-2可以得出：选模型A保留了变量LA1、LA2、LA3、YD3、YD6、GH5和GH7，即保留了是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱、乒乓球、台球、每月话费和成绩水平。除了变量成绩水平，其他变量在显著性水平*α=0.05* 下都具有统计学显著性。

4.3 基于BIC准则下的选模型B

    基于BIC准则对全模型的变量进行选择，得到选模型B，模型参数估计值如表4-3所示。

表4-3 选模型B参数估计结果

变量

Estimate

Std.Error

z value

Pr(>|z|)

(Intercept)

-2.4436

0.4708

-5.1910

2.10e-07***

LA1

1.7478

0.3423

5.1060

3.28e-07***

LA2

2.0938

0.3418

6.1260

9.02e-10***

LA3

1.3098

0.4128

3.1730

0.00151**

GH5

0.0165

0.0060

2.7440

0.00607**

    由表4-3可以得出：选模型B保留了变量LA1、LA2、LA3和GH5四个特别显著的变量，即保留了是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱和每月话费。这些变量在显著性水平*α=0.05* 下都具有较高显著性。

4.4 模型评估

  以70%的样本作为训练集，30%样本作为测试集，通过ROC曲线比较全模型和选模型A、B的分类效果，得到的三个模型的ROC曲线如图4-1所示。同时，进行随机模拟，绘制三个模型外样本AUC箱线图如图4-2所示。

图4-1 三个模型的ROC曲线

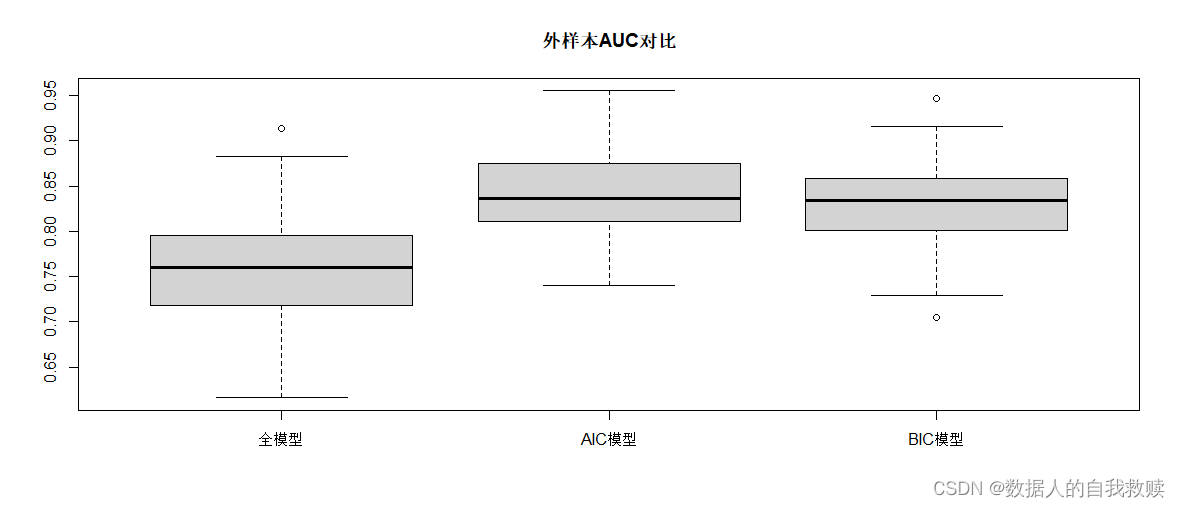
图4-2 三个模型AUC对比

  结合图4-1和图4-2可以得出：AIC模型的ROC曲线与x轴围成的面积最大，且AIC模型AUC值的箱线图最高，综合ROC曲线和AUC值可以得出，三个模型中AIC模型分类效果最好。

五、结论及建议

5.1 结论

• 被调查的学生中，大四学生最多，男女比例基本一致，大部分学生来自于二三线城市，身高介于155-185cm之间，体重介于40-70kg之间，69.3%的人戴眼镜。
• 被调查学生中，72%的人恋爱，大部分人被别人追求过且为党员，且会跑步、打羽毛球、吹乐器和唱歌。
• 用全模型对第一个受访者的恋爱概率进行预测时，当分界点α=0.5时，第一个受访者被判为不恋爱，当分界点α=0.3时，第一个受访者被判为恋爱。第一个受访者本身是不恋爱，因而α=0.5时判断正确，α=0.3时判断错误。
• 是否追求过别人、是否被别人追求过、寝室同学是否谈过恋爱和每月话费对是否恋爱由显著影响。
• 结合ROC曲线和AUC值可以得出，三个模型中AIC模型分类效果最好。

5.2 建议

  自身是否被追求过、是否追求过别人、寝室同学是否谈过恋爱和每月话费对大学生是否恋爱有显著影响。从中可以看出环境和自身意愿对是否恋爱的影响，要是想提升大学生恋爱意愿，可以加大宣传，以提升学生恋爱意愿。

六、代码

a=read.csv("D:/个人成长/学业/课程/大三下课程/统计模型/作业/第三次作业/大学生恋爱数据.csv",header=T)##读入文件
a[c(1:5),]
attach(a)
b=a[,22:32]
JB1=as.factor(JB1)
JB3=as.factor(JB3)

#统计恋爱状况
x=c(82,211)
color=c('red','orange')
piepercent1=round(100*x/sum(x),1)
pie(x,labels=piepercent1,main="是否恋爱",col=color)
legend("topright",c("否","是"),cex=0.8,fill=color)

#学生基本情况统计——年级、性别、家乡、身高、体重
x1=c(42,51,57,143)#年级
piepercent2=round(100*x1/sum(x1),1)
x2=c(144,149)#性别
piepercent3=round(100*x2/sum(x2),1)
x3=c(34,113,82,42,22)#家乡
piepercent4=round(100*x3/sum(x3),1)
par(mfrow=c(1,3))
pie(x1,labels=piepercent2,main="年级",col=rainbow(length(x1)))
legend("topright",c("大一","大二","大三","大四"),cex=1.5,fill=rainbow(length(x1)))
pie(x2,labels=piepercent3,main="性别",col=color)
legend("topright",c("男","女"),cex=1.5,fill=color)
pie(x3,labels=piepercent4,main="家乡",col=rainbow(length(x3)))
legend("topright",c("一线城市","二线城市","三线城市","县级市","农村"),cex=1.5,fill=rainbow(length(x3)))
#学生身高体重统计
par(mfrow=c(1,2))
hist(a$身高,main="身高",xlab="组别" ,ylab = "频数")#直方图
hist(a$体重,main="体重",xlab="组别" ,ylab = "频数")#直方图

#学生恋爱史统计
y1=c(134,159)#是否追求过别人
piepercent11=round(100*y1/sum(y1),1)
y2=c(75,218)#是否被别人追求过
piepercent12=round(100*y2/sum(y2),1)
y3=c(205,88)#寝室同学是否谈过恋爱
piepercent13=round(100*y3/sum(y3),1)
par(mfrow=c(1,3))
pie(y1,labels=piepercent11,main="是否追求过别人",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(y2,labels=piepercent12,main="是否被别人追求过",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(y3,labels=piepercent13,main="寝室同学是否谈过恋爱",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)

#学生职务担任情况
z1=c(101,192)#班干部
piepercent21=round(100*z1/sum(z1),1)
z2=c(239,54)#党员
piepercent22=round(100*z2/sum(z2),1)
par(mfrow=c(1,2))
pie(z1,labels=piepercent21,main="班干部",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(z2,labels=piepercent22,main="党员",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)

#学生运动情况
w1=c(257,36)#足球
piepercent31=round(100*w1/sum(w1),1)
w2=c(227,66)#篮球
piepercent32=round(100*w2/sum(w2),1)
w3=c(229,64)#乒乓球
piepercent33=round(100*w3/sum(w3),1)
w4=c(168,125)#羽毛球
piepercent34=round(100*w4/sum(w4),1)
w5=c(144,149)#跑步
piepercent35=round(100*w5/sum(w5),1)
w6=c(220,73)#台球
piepercent36=round(100*w6/sum(w6),1)
par(mfrow=c(2,3))
pie(w1,labels=piepercent31,main="足球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w2,labels=piepercent32,main="篮球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w3,labels=piepercent33,main="乒乓球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w4,labels=piepercent34,main="羽毛球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w5,labels=piepercent35,main="跑步",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(w6,labels=piepercent36,main="台球",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)

#学生才艺情况
v1=c(195,98)#唱歌
piepercent41=round(100*v1/sum(v1),1)
v2=c(270,23)#主持
piepercent42=round(100*v2/sum(v2),1)
v3=c(268,25)#舞蹈
piepercent43=round(100*v3/sum(v3),1)
v4=c(180,110)#乐器
piepercent44=round(100*v4/sum(v4),1)
v5=c(133,160)#其他才艺
piepercent45=round(100*v5/sum(v5),1)
par(mfrow=c(2,3))
pie(v1,labels=piepercent41,main="唱歌",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v2,labels=piepercent42,main="主持",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v3,labels=piepercent43,main="舞蹈",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v4,labels=piepercent44,main="乐器",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
pie(v5,labels=piepercent45,main="其他才艺",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)

#学生颜值情况
t1=c(90,203)#是否戴眼镜
piepercent51=round(100*t1/sum(t1),1)
par(mfrow=c(1,2))
pie(t1,labels=piepercent51,main="是否戴眼镜",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
hist(a$颜值,main="颜值",xlab="组别" ,ylab = "频数")#直方图

#学生生活规划情况
par(mfrow=c(2,4))
hist(a$每周自习时间,main="每周自习时间",xlab="组别" ,ylab = "频数")
hist(a$每周娱乐时间,main="每周娱乐时间",xlab="组别" ,ylab = "频数")
hist(a$每周睡觉时间,main="每周睡觉时间",xlab="组别" ,ylab = "频数")
hist(a$每周运动时间,main="每周运动时间",xlab="组别" ,ylab = "频数")
hist(a$每月话费,main="每月话费",xlab="组别" ,ylab = "频数")
hist(a$学生组织个数,main="学生组织个数",xlab="组别" ,ylab = "频数")
hist(a$成绩水平,main="成绩水平",xlab="组别" ,ylab = "频数")
hist(a$生活费_百元,main="生活费_百元",xlab="组别" ,ylab = "频数")

#连续变量之间相关性热力图
library(corrplot)
k=cor(b,use='everything',method='pearson')
par(mfrow=c(1,1))
corrplot(k,addCoef.col = "black")

#绘制箱线图
par(mfrow=c(2,4))
boxplot(a$每周自习时间~a$是否恋爱,ylab="每周自习时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每周娱乐时间~a$是否恋爱,ylab="每周娱乐时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每周睡觉时间~a$是否恋爱,ylab="每周睡觉时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每周运动时间~a$是否恋爱,ylab="每周运动时间",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$每月话费~a$是否恋爱,ylab="每月话费",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$学生组织个数~a$是否恋爱,ylab="学生组织个数",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$成绩水平~a$是否恋爱,ylab="成绩水平",xlab="是否恋爱",data=a,names=c("否","是"))
boxplot(a$生活费_百元~a$是否恋爱,ylab="生活费_百元",xlab="是否恋爱",data=a,names=c("否","是"))

#全模型
model.full=glm(Y~as.factor(JB1)+JB2+as.factor(JB3)+JB4+JB5+LA1+LA2+LA3+ZW1+ZW2+YD1+YD2+YD3+YD4+YD5+YD6+CY1+
                 CY2+CY3+CY4+CY5+YZ1+YZ2+GH1+GH2+GH3+GH4+GH5+GH6+GH7+GH8,family=binomial(link=logit),data=a)
#模型结果，不显著的变量也要解读，加上不具有统计学意义
summary(model.full)
#似然比卡方检验模型整体效果
1-pchisq(30.56,df=7)

pred=predict(model.full,a)

#基于AIC准则下变量的选择
c(AIC(model.full),BIC(model.full))
model.aic=step(model.full,trace = F)
summary(model.aic)
ss=length(a[,1])#样本量
#基于BIC准则下变量的选择
model.bic=step(model.full,trace = F,k=log(ss))
summary(model.bic)
#只留了特别显著的变量

library(pROC)
#多次模拟，去除随机误差的影响（了解即可）
nsimu=100#进行100次模拟
p=0.7#用作训练集的样本概率
ss0=round(ss*p)#训练集样本量
AUC=as.data.frame(matrix(0,nsimu,3))#100行，3列的零数据框
names(AUC)=c("全模型","AIC模型","BIC模型")
#开始模拟
for(i in 1:nsimu){
  #打乱a样本顺序，随即编号并排序
  aa=a[order(runif(ss)),]
  #数据集aa的前70%作为训练集
  A0=aa[c(1:ss0),]
  #数据集aa的后30%作为测试集
  A1=aa[-c(1:ss0),]
  
  model.1=glm(Y~as.factor(JB1)+JB2+as.factor(JB3)+JB4+JB5+LA1+LA2+LA3+ZW1+ZW2+YD1+YD2+YD3+YD4+YD5+YD6+CY1+
                CY2+CY3+CY4+CY5+YZ1+YZ2+GH1+GH2+GH3+GH4+GH5+GH6+GH7+GH8,family=binomial(link=logit),data=A0)
  model.2=glm(Y~LA1+LA2+LA3+YD3+YD6+GH5+GH7,family=binomial(link=logit),data=A0)
  model.3=glm(Y~LA1+LA2+LA3+GH5,family=binomial(link=logit),data=A0)
  
  #测试集检验模型效果，计算预测值
  pred.1=predict(model.1,A1)
  pred.2=predict(model.2,A1)
  pred.3=predict(model.3,A1)
  
  #计算AUC值
  y=A1$Y
  auc.1=roc(y,pred.1)$auc
  auc.2=roc(y,pred.2)$auc
  auc.3=roc(y,pred.3)$auc
  
  #将各个AUC值填充到零矩阵中
  AUC[i,]=c(auc.1,auc.2,auc.3)
}
#绘制箱线图看三个模型的AUC分布情况，AUC越大，模型分类效果越好
par(mfrow=c(1,1))
boxplot(AUC,main="外样本AUC对比")
#利用最后一次模拟数据绘制三个模型的ROC曲线
#计算混淆矩阵
roc.1=roc(y,pred.1)
roc.2=roc(y,pred.2)
roc.3=roc(y,pred.3)
#绘制三条ROC曲线，比较效果
par(mfrow=c(1,3))
plot(roc.1,main="全模型")
plot(roc.2,main="AIC模型")
plot(roc.3,main="BIC模型")

---

个人反思：描述性统计饼图过小，可以直接用一个表格计算出百分比即可，不必画这么多饼图

个人意见，还请各位读者批评指正！