理解控制变量、内生变量、外生变量、工具变量

文章目录

前言

1.解释变量（或自变量）：解释变量是指作为研究对象，用于解释某个现象或行为模式的变量。其中有些解释变量是直接影响被解释变量的，有些则是间接或中介影响的。在回归分析中，解释变量通常被放在方程的右边。

2.被解释变量（或因变量）：被解释变量是指通过解释变量来解释其变化产生的影响的变量，也可以称为因变量。在回归分析中，被解释变量通常被放在方程的左边。

3.控制变量（或干扰变量）：控制变量是指在控制所研究的解释变量和被解释变量之间的关系时，需要控制的可能具有影响的变量。例如，我们希望研究教育对收入的影响，但同时需要将一些其他因素（例如性别、年龄、工作经验等）视为控制变量。通过对这些变量进行控制，可以更准确地估计教育对收入的影响。

一、控制变量

先看一个例子：
理解：喝可乐会变胖吗？
控制：其他与特征相关的因素没，比如：

锻炼强度

、

日常饮食

、

年龄

…
实验设计：
保证实验组（treatment group）和控制组（control group）
锻炼强度相同、饮食相同，年龄相同等其他因素。

解释：
在计量经济学中，控制变量是指通过对所研究的因素进行控制，来消除可能影响研究变量之间关系的其他因素。具体来讲，研究者想要控制某个变量时，就要尽可能地与其他可能的影响因素（控制变量）隔离，以便能够更准确地研究所需的变量之间的关系。

例如，假设我们想研究吸烟与肺癌之间的关系。为了消除其他因素对这种关系的影响，我们需要控制一些变量，如年龄、遗传因素、长期吸入有害气体等等。通过对这些变量进行控制，我们可以更加准确地估计出吸烟和肺癌之间的关系。
为什么要控制：如果不控制模型会生病，结论不可靠，估计参数有偏，产生内生性。
怎么确定控制变量：看前人的研究，找相关文献。

二、内生变量、外生变量

举个例子
有一个模型简单表达为：

      Y 
     
    
      = 
     
    
      a 
     
    
      + 
     
    
      b 
     
    
      X 
     
    
      + 
     
    
      ϵ 
     
    
   
     Y=a+bX+\epsilon 
    
   
 Y=a+bX+ϵ

内生变量：Y、X，模型决定的，也就是因变量、自变量。
外生变量：a,b，模型外的因素决定的，已知的，参数。
通常由

内生性决定外生性

在计量经济学中，我们经常把变量分为内生变量和外生变量。

内生变量是指模型中的被解释变量或者解释变量，与其他变量的因果关系存在研究偏误和混淆的可能性，是需要解释和控制的变量。

举个例子，假设我们研究驾驶员的车祸率与使用手机的频率之间的关系。在这个模型中，车祸率是被解释变量，而使用手机的频率是解释变量。然而，这个模型的研究结果可能存在研究偏误，因为许多其他因素可能会影响车祸率，比如驾驶员的年龄、性别、驾驶经验等等。因此，这些影响车祸率的因素就是内生变量。

在计量经济学中，外生变量是指对被研究现象或行为结果有影响，但不受研究对象影响的变量。这些变量是在研究要素之外并且在研究对象之前就存在的，通常是定量测量的，其值不依赖于被研究的行为或结果。

举例来说，对于一个销售额的研究，外生变量可能包括经济总体，竞争对手行业的价格和促销活动，天气，人口统计学数据等因素。这些变量不受销售团队的控制，但会对销售额产生影响。

区分内生性

内生性：模型中一个变量或多个变量与随机扰动项相关
理解：
假设这是一个真实无误的模型：

      Y 
     
    
      = 
     
     
     
       β 
      
     
       1 
      
     
     
     
       X 
      
     
       1 
      
     
    
      + 
     
     
     
       β 
      
     
       2 
      
     
     
     
       X 
      
     
       2 
      
     
    
      + 
     
    
      μ 
     
    
   
     Y=\beta_1X_1+\beta_2X_2+\mu 
    
   
 Y=β1​X1​+β2​X2​+μ

且

      β 
     
    
      1 
     
    
   
     = 
    
   
     1 
    
   
  
    \beta_1=1 
   
  
β1​=1， 
 
  
   
    
    
      β 
     
    
      2 
     
    
   
     = 
    
   
     1 
    
   
  
    \beta_2=1 
   
  
β2​=1， 
 
  
   
   
     c 
    
   
     o 
    
   
     v 
    
   
     ( 
    
    
    
      X 
     
    
      1 
     
    
   
     , 
    
    
    
      X 
     
    
      2 
     
    
   
     ) 
    
   
     = 
    
   
     0.5 
    
   
  
    cov(X_1,X_2)=0.5 
   
  
cov(X1​,X2​)=0.5

但你的估计模型却是：

      Y 
     
    
      = 
     
     
     
       β 
      
     
       1 
      
     
     
     
       X 
      
     
       1 
      
     
    
      + 
     
    
      ϵ 
     
    
   
     Y= \beta_1X_1+\epsilon 
    
   
 Y=β1​X1​+ϵ

如果，

      X 
     
    
      1 
     
    
   
  
    X_1 
   
  
X1​变动1单位，真实情况下， 
 
  
   
    
    
      X 
     
    
      2 
     
    
   
  
    X_2 
   
  
X2​会变0.5，带入真实模型， 
 
  
   
   
     Y 
    
   
     = 
    
   
     1.5 
    
   
  
    Y=1.5 
   
  
Y=1.5

这是，你的估计模型

      β 
     
    
      1 
     
    
   
  
    \beta_1 
   
  
β1​的估计系数却为1.5，真实的为 
 
  
   
    
    
      β 
     
    
      1 
     
    
   
     = 
    
   
     1 
    
   
  
    \beta_1=1 
   
  
β1​=1

这就造成了偏误。
这就是遗漏变量造成的内生性
常见造成内生性的原因以及处理方式
见B站大佬-

内生性处理方式总结【传送门】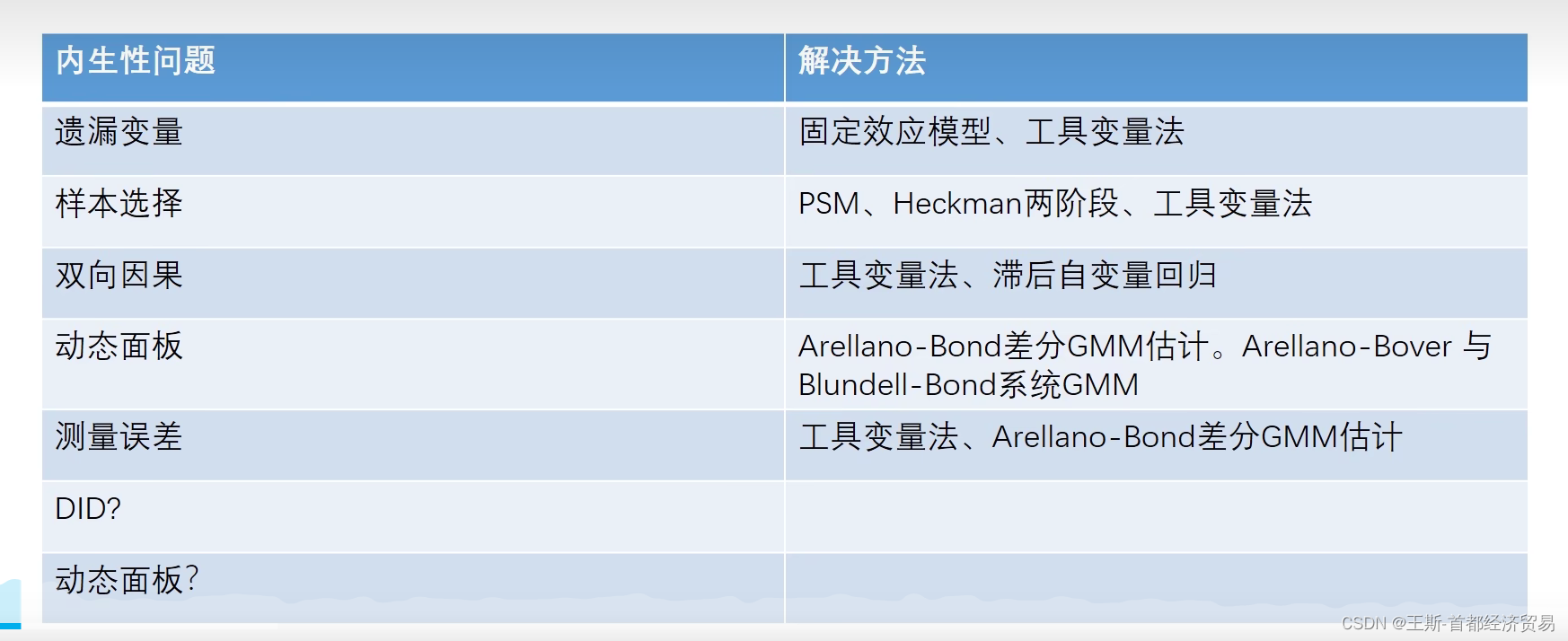

三、工具变量（IV）

工具变量由工具变量法引入，其实是一种方法。
在某些情况下，模型中的某个变量可能受到未观测到的外部因素的影响，这就会造成内生性问题。为了解决这个问题，我们可以引入一个工具变量，它与内生变量相关，但与模型中其他变量无关。

这是1)、2)满足工具变量的两个条件.
举个例子，假设我们想研究健康对收入的影响，但是健康本身很可能会受到其他因素（例如遗传、家庭背景等）的影响，从而对收入产生间接的影响，
我们可以使用居住地的污染水平作为工具变量，来解决这个问题。通过引入污染水平作为工具变量，我们可以确保收入被正确地归因于健康，从而避免了内生性问题。