独孤九剑第四式-K近邻模型(KNN)

💐文章适合于所有的相关人士进行学习💐
🍀各位看官看完了之后不要立刻转身呀🍀
🌿期待三连关注小小博主加收藏🌿
🍃小小博主回关快 会给你意想不到的惊喜呀🍃
各位老板动动小手给小弟点赞收藏一下，多多支持是我更新得动力！！！

文章目录

🐢前言

我们已经讲解完了线性回归，包括一元线性回归和多重线性回归模型，然后在这个基础之上我们又讲解了岭回归和Lasso回归模型，然后是Logistic回归模型，上次我们讲了决策树和随即森林的相关知识，我们这节课讲解KNN，K近邻模型，那么什么是K近邻模型呢？字面意思：你的邻居。就是离你住的地方比较近的东西。其实这就是K近邻中的近邻的意思。

🐢KNN理论讲解

🐧模型思想

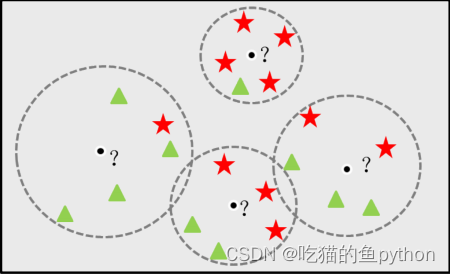
我们看这个图，？表示我们不知道是什么的点，其实也就是我们想要预测的点，这个时候我们就要定义一个K值，也就是我找到离我最近的K个邻居，然后我看这K个邻居当中都是什么，我们以最左边的这个为例子，有4个邻居是绿色的，一个邻居是红色的，那么根据投票法，我们就将？部分预测为绿色的。
我们对于离散型变量，从最近的K个样本中挑选出频率最高的样本作为预测结果。对于连续型变量将k个最近的样本均值作为最后的预测结果。这里很好理解。

🐧确定K值

那么我们如何确定这个K值呢，K值又对我们的预测结果有什么影响呢？我们先说为什么要确定K值，因为K值定的比较小，就说明我就找我附近几个作为参考，那么就有可能过拟合，就是说什么意思呢？我本来不是红色，但是我旁边偏偏就有两个红色，其他的都是绿色，那么我就预测为红色，那么这是不准确的。如果K值定的过大，那么模型比较简单，就很难将正确的分出来。就会欠拟合。具体如下图：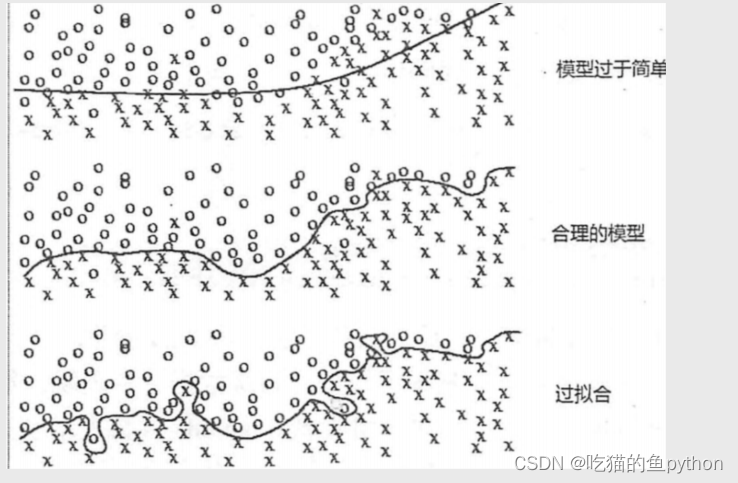

所以我们在做模型的预测时一定要先把K值确定下来，那么我们如何确定呢？
第一种方法就是我们通过设置权重的方式来解决：
设置k近邻样本的投票权重，使用KNN算法进行分类或预测时设置的k值比较大，担心模型发生欠拟合的现象，一个简单有效的处理办法就是设置近邻样本的投票权重，如果已知样本距离未知样本比较远，则对应的权重就设置得低一些，否则权重就高一些，通常可以将权重设置为距离的倒数。
第二种方法就是多重交叉验证法：
我们之前也学过10重交叉验证法这种方式来去解决选择参数这个问题，那么这个K值得选择我们也可以进行这样选择，方式就是我们对于每一个K值，都进行多重交叉验证。每一重都选出计算出其平均误差，然后进行比较就得出了最后得K值。
当然后也可以这两种方法结合使用。
这里我们直接穿插代码看一下：

import numpy as np
from sklearn import neighbors
import matplotlib.pyplot as plt

# 设置K得数值，定义为int类型也就是整形
K = np.arange(1,np.ceil(np.log2(Knowledge.shape[0]))).astype(int)# 存储平均准确率
accuracy =[]for k in K:# 使用交叉验证的方法，比对每一个k值下KNN模型的预测准确率
    cv_result = model_selection.cross_val_score(neighbors.KNeighborsClassifier(n_neighbors = k, weights ='distance'), 
                                                X_train, y_train, cv =10, scoring='accuracy')
    accuracy.append(cv_result.mean())# 从k个平均准确率中挑选出最大值所对应的下标    
arg_max = np.array(accuracy).argmax()# 中文和负号的正常显示
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
plt.rcParams['axes.unicode_minus']=False# 绘制不同K值与平均预测准确率之间的折线图
plt.plot(K, accuracy)# 添加点图
plt.scatter(K, accuracy)# 添加文字说明
plt.text(K[arg_max], accuracy[arg_max],'最佳k值为%s'%int(K[arg_max]))# 显示图形
plt.show()

最后生成得图形结果是：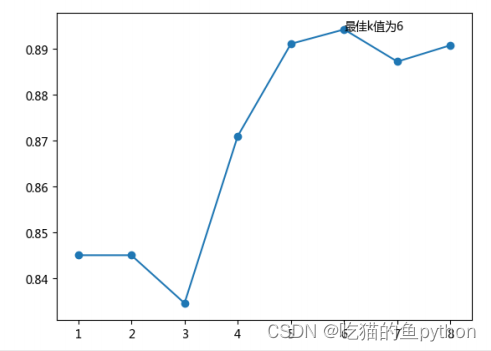

由此我们就可以知道K得最佳数值是6.然后我们把6带入到预测得过程当中进行预测。
然后还有一个就是我们得邻居和邻居间的距离怎么算，都有什么？

🐔欧氏距离

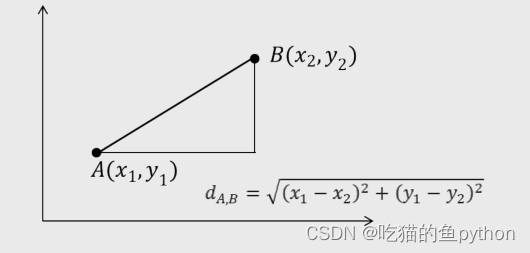
我们常说得欧氏距离其实就是我们初中学过得两点之间得距离公式，这个没有什么好解释得。都懂！！！

🐔曼哈顿距离

那么什么是曼哈顿距离，据我了解，我所了解到的涉及到曼哈顿距离中很大一部分都在迷宫问题中出现，就是表示有障碍物体这种，然后使用曼哈顿距离公式。具体如图：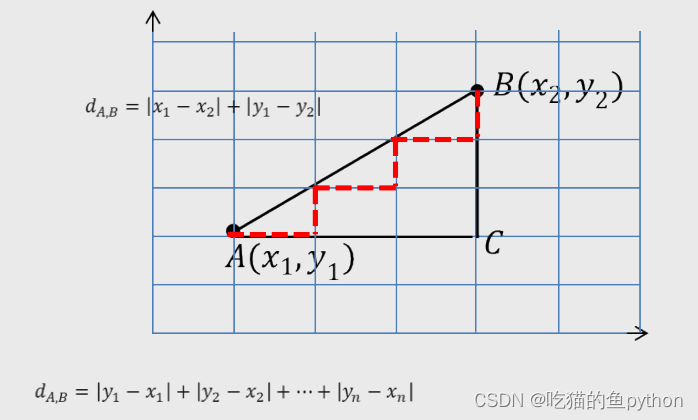

图呢也简单易懂，直接拿捏！

🐔余弦相似度

这种我们在高中得时候也学习过，也非常简单！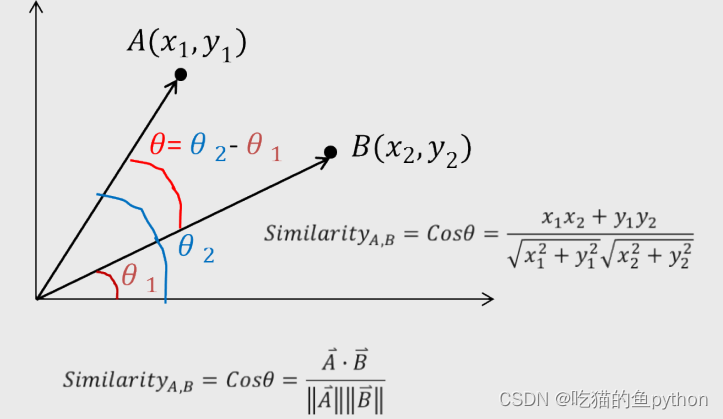

这就是我们总结得三种计算距离得公式了，那么万事具备，来东风！！！

🐢实战演练

🐧数据展示

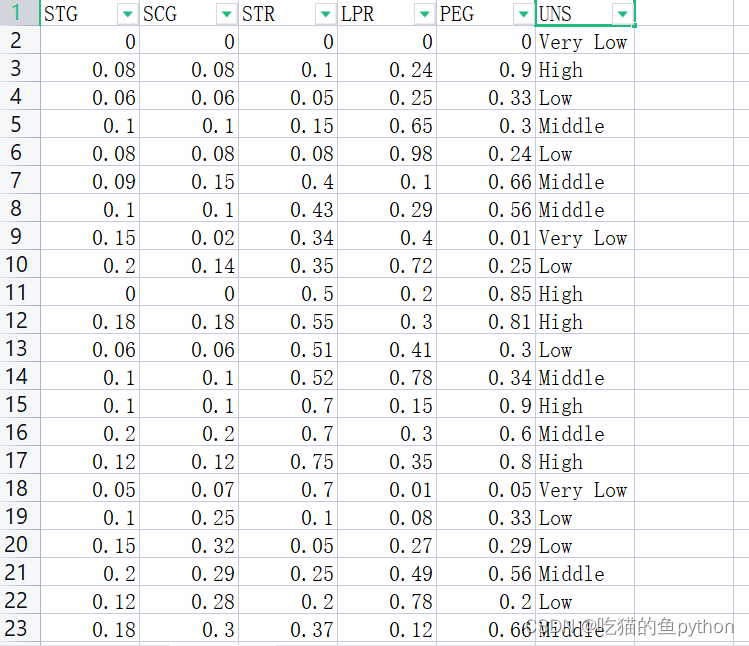
🐧读入

import pandas as pd
Knowledge = pd.read_excel(r'Knowledge.xlsx')
Knowledge.head()

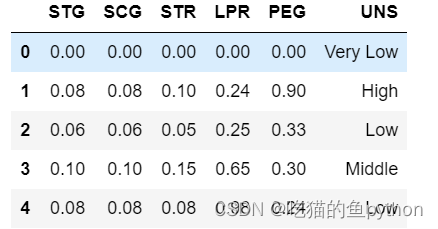
🐧拆分为训练集和测试集

from sklearn import model_selection
# 将数据集拆分为训练集和测试集
predictors = Knowledge.columns[:-1]
X_train, X_test, y_train, y_test = model_selection.train_test_split(Knowledge[predictors], Knowledge.UNS, 
                                                                    test_size =0.25, random_state =1234)

🐧确定K值

import numpy as np
from sklearn import neighbors
import matplotlib.pyplot as plt

# 设置K得数值，定义为int类型也就是整形
K = np.arange(1,np.ceil(np.log2(Knowledge.shape[0]))).astype(int)# 存储平均准确率
accuracy =[]for k in K:# 使用交叉验证的方法，比对每一个k值下KNN模型的预测准确率
    cv_result = model_selection.cross_val_score(neighbors.KNeighborsClassifier(n_neighbors = k, weights ='distance'), 
                                                X_train, y_train, cv =10, scoring='accuracy')
    accuracy.append(cv_result.mean())# 从k个平均准确率中挑选出最大值所对应的下标    
arg_max = np.array(accuracy).argmax()# 中文和负号的正常显示
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
plt.rcParams['axes.unicode_minus']=False# 绘制不同K值与平均预测准确率之间的折线图
plt.plot(K, accuracy)# 添加点图
plt.scatter(K, accuracy)# 添加文字说明
plt.text(K[arg_max], accuracy[arg_max],'最佳k值为%s'%int(K[arg_max]))# 显示图形
plt.show()

结果同上！

🐧构造混淆矩阵

from sklearn import metrics

# 重新构建模型，并将最佳的近邻个数设置为6
knn_class = neighbors.KNeighborsClassifier(n_neighbors =6, weights ='distance')#权重设置为距离
knn_class.fit(X_train, y_train)
predict = knn_class.predict(X_test)
cm = pd.crosstab(predict,y_test)
cm#构造混淆矩阵

🐧热力图

import seaborn as sns

# 将混淆矩阵构造成数据框，并加上字段名和行名称，用于行或列的含义说明
cm = pd.DataFrame(cm)
sns.heatmap(cm, annot =True,cmap ='GnBu')
plt.xlabel(' Real Lable')
plt.ylabel(' Predict Lable')
plt.show()

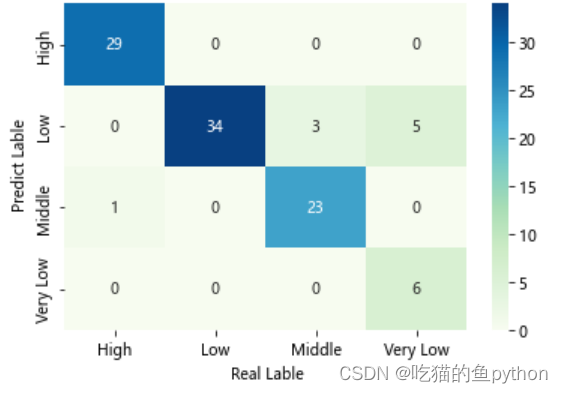
模型得准确率最终确定为：0.91
模型评估报告。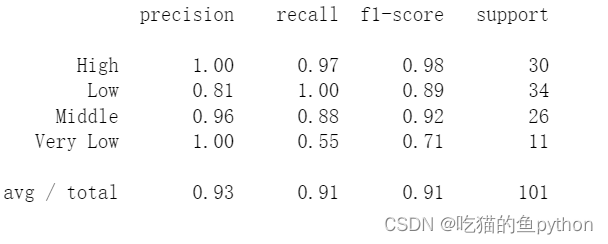

💐文章适合于所有的相关人士进行学习💐
🍀各位看官看完了之后不要立刻转身呀🍀
🌿期待三连关注小小博主加收藏🌿
🍃小小博主回关快 会给你意想不到的惊喜呀🍃
各位老板动动小手给小弟点赞收藏一下，多多支持是我更新得动力！！！