强化学习（四）—— Actor-Critic

强化学习（四）—— Actor-Critic

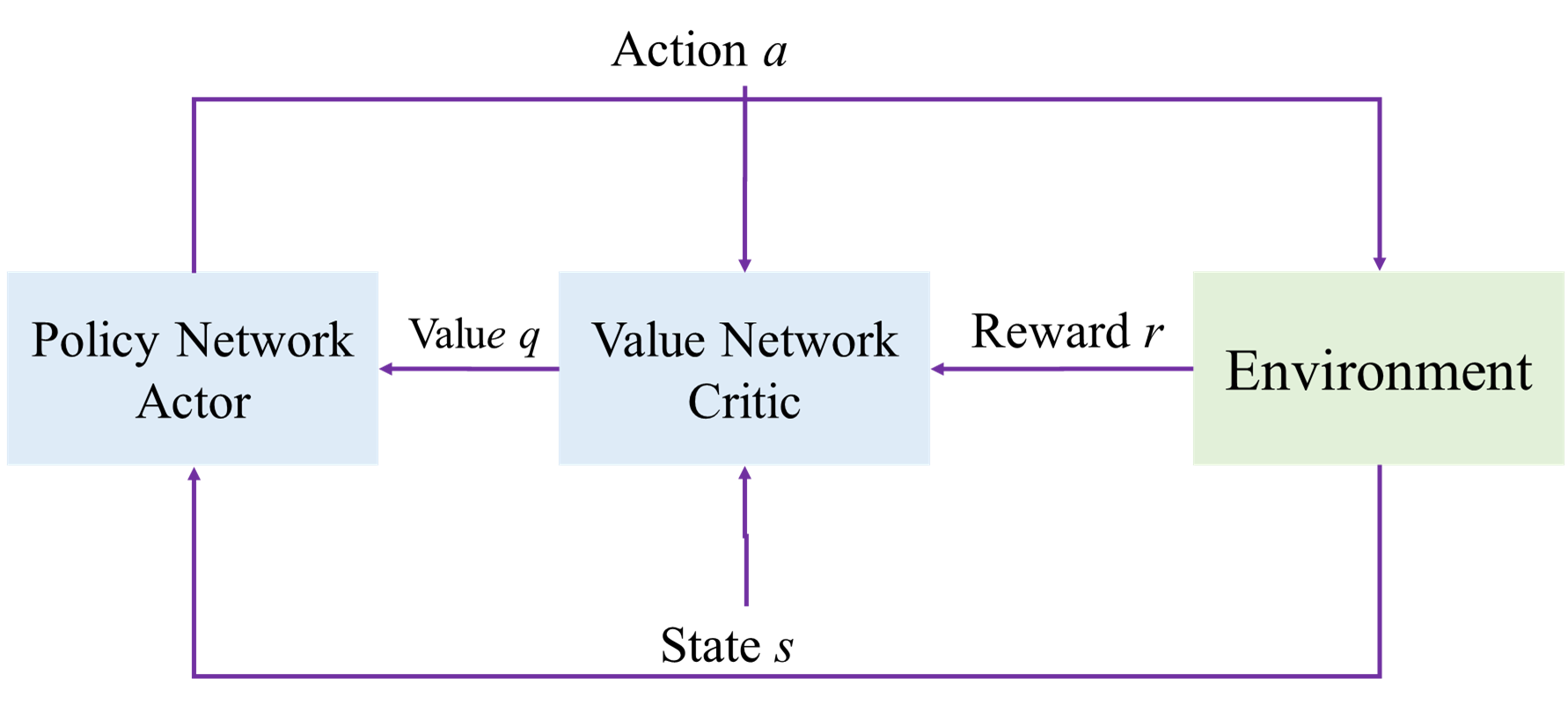
1. 网络结构

• 状态价值函数： V π ( s t ) = ∑ a Q π ( s t , a ) ⋅ π ( a ∣ s t ) V_\pi(s_t)=\sum_aQ_\pi(s_t,a)\cdot\pi(a|s_t) Vπ​(st​)=a∑​Qπ​(st​,a)⋅π(a∣st​)
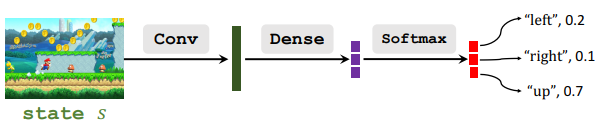
• 通过策略网络近似策略函数: π ( a ∣ s ) ≈ π ( a ∣ s ; θ ) \pi(a|s)\approx\pi(a|s;\theta) π(a∣s)≈π(a∣s;θ)
• 通过价值网络近似动作价值函数: q ( s , a ; W ) ≈ Q ( s , a ) q(s,a;W)\approx Q(s,a) q(s,a;W)≈Q(s,a)
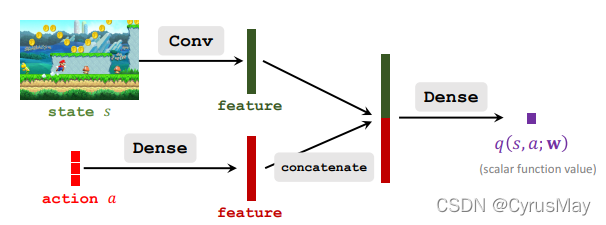
• 神经网络近似后的状态价值函数: V ( s ; θ , W ) = ∑ a q ( s , a ; W ) ∗ π ( a ∣ s ; θ ) V(s;\theta ,W)=\sum_aq(s,a;W)*\pi(a|s;\theta) V(s;θ,W)=a∑​q(s,a;W)∗π(a∣s;θ)
• 通过对策略网络不断更新以增加状态价值函数值。
• 通过对价值网络不断更新来更好的预测所获得的回报。

2. 网络函数

Policy Network

• 通过策略网络近似策略函数 π ( a ∣ s t ) ≈ π ( a ∣ s t ; θ ) π(a|s_t)≈π(a|s_t;\theta) π(a∣st​)≈π(a∣st​;θ)
• 状态价值函数及其近似 V π ( s t ) = ∑ a π ( a ∣ s t ) Q π ( s t , a ) V_π(s_t)=\sum_aπ(a|s_t)Q_π(s_t,a) Vπ​(st​)=a∑​π(a∣st​)Qπ​(st​,a) V ( s t ; θ ) = ∑ a π ( a ∣ s t ; θ ) ⋅ Q π ( s t , a ) V(s_t;\theta)=\sum_aπ(a|s_t;\theta)·Q_π(s_t,a) V(st​;θ)=a∑​π(a∣st​;θ)⋅Qπ​(st​,a)
• 策略学习最大化的目标函数 J ( θ ) = E S [ V ( S ; θ ) ] J(\theta)=E_S[V(S;\theta)] J(θ)=ES​[V(S;θ)]
• 依据策略梯度上升进行 θ ← θ + β ⋅ ∂ V ( s ; θ ) ∂ θ \theta\gets\theta+\beta·\frac{\partial V(s;\theta)}{\partial \theta} θ←θ+β⋅∂θ∂V(s;θ)​

3. 策略网络的更新-策略梯度

Policy Network

• 策略梯度为： g ( a , θ ) = ∂ l n π ( a ∣ s ; θ ) ∂ θ ⋅ q ( s , a ; W ) ∂ V ( s ; θ , W ) ∂ θ = E [ g ( A , θ ) ] g(a,\theta)=\frac{\partial ln\pi(a|s;\theta)}{\partial \theta}\cdot q(s,a;W)\\frac{\partial V(s;\theta,W)}{\partial \theta}=E[g(A,\theta)] g(a,θ)=∂θ∂lnπ(a∣s;θ)​⋅q(s,a;W)∂θ∂V(s;θ,W)​=E[g(A,θ)]
• 可采用随机策略梯度，（无偏估计） a ∼ π ( ⋅ ∣ s t ; θ ) θ t + 1 = θ t + β ⋅ g ( a , θ t ) a\sim \pi(\cdot|s_t;\theta)\\theta_{t+1}=\theta_t+\beta·g(a,\theta_t) a∼π(⋅∣st​;θ)θt+1​=θt​+β⋅g(a,θt​)

4. 价值网络的更新-时序差分（TD）

• TD的目标： y t = r t + γ q ( s t + 1 , a t + 1 ; W t ) y_t= r_t+\gamma q(s_{t+1},a_{t+1};W_t) yt​=rt​+γq(st+1​,at+1​;Wt​)
• 损失函数为： l o s s = 1 2 [ q ( s t , a t ; W t ) − y t ] 2 loss = \frac{1}{2}[q(s_t,a_t;W_t)-y_t]^2 loss=21​[q(st​,at​;Wt​)−yt​]2
• 采用梯度下降进行更新： W t + 1 = W t − α ⋅ ∂ l o s s ∂ W ∣ W = W t W_{t+1}=W_t-\alpha\cdot\frac{\partial loss}{\partial W}|_{W=W_t} Wt+1​=Wt​−α⋅∂W∂loss​∣W=Wt​​

5. 网络训练流程

一次更新中，Agent执行一次动作，获得一次奖励。

1. 获得状态st并随机采样动作： a t ∼ π ( ⋅ ∣ s t ; θ ) a_t \sim\pi(\cdot|s_t;\theta) at​∼π(⋅∣st​;θ)
2. Agent执行动作，并获得环境的新状态和奖励： s t + 1 r t s_{t+1}\r_t st+1​rt​
3. 依据新状态再次随机采样动作（该动作在本次迭代中并不执行）： a ~ t + 1 ∼ π ( ⋅ ∣ s t + 1 ; θ ) \tilde{a}{t+1}\sim\pi(\cdot|s{t+1};\theta) a~t+1​∼π(⋅∣st+1​;θ)
4. 依据价值网络，分别计算两个动作和状态的价值： q t = q ( s t , a t ; W t ) q t + 1 = q ( s t + 1 , a ~ t + 1 ; W t ) q_t=q(s_t,a_t;W_t)\q_{t+1}=q(s_{t+1},\tilde{a}_{t+1};W_t) qt​=q(st​,at​;Wt​)qt+1​=q(st+1​,a~t+1​;Wt​)
5. 计算TD误差： δ t = q t − ( r t + γ q t + 1 ) \delta_t=q_t-(r_t+\gamma q_{t+1}) δt​=qt​−(rt​+γqt+1​)
6. 计算价值网络的导数： d W , t = ∂ q ( s t , a t ; W ) ∂ W ∣ W = W t d_{W,t}=\frac{\partial q(s_t,a_t;W)}{\partial W}|_{W=W_t} dW,t​=∂W∂q(st​,at​;W)​∣W=Wt​​
7. 对价值网络进行梯度更新： W t + 1 = W t − α ⋅ δ t ⋅ d W , t W_{t+1}=W_t-\alpha\cdot\delta_t\cdot d_{W,t} Wt+1​=Wt​−α⋅δt​⋅dW,t​
8. 计算策略网络的梯度： d θ , t = ∂ l n [ π ( ⋅ ∣ s t ; θ ) ] ∂ θ ∣ θ = θ t d_{\theta,t}=\frac{\partial ln[\pi(\cdot|s_t;\theta)]}{\partial\theta}|_{\theta=\theta_t} dθ,t​=∂θ∂ln[π(⋅∣st​;θ)]​∣θ=θt​​
9. 对策略网络进行梯度更新,式（2）为式（1）对动作价值函数值使用了baseline，目标函数的期望一致，但是方差减小，网络更容易收敛。 θ t + 1 = θ + β ⋅ q t ⋅ d θ , t θ t + 1 = θ + β ⋅ δ t ⋅ d θ , t \theta_{t+1}=\theta+\beta\cdot q_t\cdot d_{\theta,t}\\theta_{t+1}=\theta+\beta\cdot \delta_t\cdot d_{\theta,t} θt+1​=θ+β⋅qt​⋅dθ,t​θt+1​=θ+β⋅δt​⋅dθ,t​

6. 案例

该网络的收敛对于模型大小、激活函数等参数较敏感。

# -*- coding: utf-8-*-
# @Time :2022/3/2921:51
# @Author : CyrusMay WJ
# @FileName:AC.py
# @Software: PyCharm
# @Blog ：https://blog.csdn.net/Cyrus_May

import tensorflow as tf
import numpy as np
import logging
import sys
import gym

classCritic():
    def __init__(self,logger=None,input_dim=6,gamma=0.9):
        self.logger = logger
        self.__build_model(input_dim)
        self.gamma = gamma
        self.optimizer = tf.optimizers.Adam(learning_rate=0.001)

    def __build_model(self,input_dim):
        self.model = tf.keras.Sequential([
            tf.keras.layers.Dense(32, activation="relu"),
            tf.keras.layers.Dense(1)])
        self.model.build(input_shape=[None,input_dim])

    def predict(self,action,state):
        action = tf.one_hot([action],depth=2)
        state = tf.convert_to_tensor([state])
        x = tf.concat([action,state],axis=1)return self.model(x)[0][0]

    def train(self,state,state_,action,action_,reward,done):
        action = tf.one_hot([action], depth=2)
        state = tf.convert_to_tensor([state])
        action_ = tf.one_hot([action_], depth=2)
        state_ = tf.convert_to_tensor([state_])
        x = tf.concat([action, state], axis=1)
        x_ = tf.concat([action_, state_], axis=1)
        done =0if done else1with tf.GradientTape()as tape:
            q = self.model(x)
            q_ = self.model(x_)
            Td_error =(reward + done * self.gamma * q_ - q)
            loss = tf.square(Td_error)
            dt = tape.gradient(loss,self.model.trainable_variables)
        self.optimizer.apply_gradients(zip(dt,self.model.trainable_variables))return Td_error

classActor():
    def __init__(self,logger=None,input_dim=4,gamma=0.9,output_dim=2):
        self.logger = logger
        self.__build_model(input_dim,output_dim)
        self.gamma = gamma
        self.optimizer = tf.optimizers.Adam(learning_rate=0.001)
        self.output_dim = output_dim

    def __build_model(self,input_dim,output_dim=2):
        self.model = tf.keras.Sequential([
            tf.keras.layers.Dense(32, activation="relu"),
            tf.keras.layers.Dense(output_dim)])
        self.model.build(input_shape=[None,input_dim])
    def predict(self,state):
        state = tf.convert_to_tensor([state])
        logits = self.model(state)
        prob = tf.nn.softmax(logits).numpy()
        action = np.random.choice([i for i inrange(self.output_dim)],p=prob.ravel())return action

    def train(self,state,action,TD_error,done):
        state = tf.convert_to_tensor([state])with tf.GradientTape()as tape:
            logits = self.model(state)
            loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels =[action], logits=logits)
            loss = tf.reduce_sum(tf.multiply(TD_error,loss))
            dt = tape.gradient(loss,self.model.trainable_variables)
            self.optimizer.apply_gradients(zip(dt,self.model.trainable_variables))classAgent():
    def __init__(self,gamma=0.9,logger=None):
        self.gamma = gamma
        self.logger = logger
        self.env = gym.make("CartPole-v0")
        self.actor =Actor(logger=logger,input_dim=4,gamma=self.gamma,output_dim=2)
        self.critic =Critic(logger = logger,input_dim=6,gamma=self.gamma)

    def train(self,tran_epochs=1000,max_act=100):
        history_returns =[]for epoch inrange(tran_epochs):
            single_returns =0
            state = self.env.reset()for iter inrange(max_act):
                self.env.render()
                action = self.actor.predict(state)
                state_,reward,done,info = self.env.step(action)
                action_  = self.actor.predict(state_)
                TD_error = self.critic.train(state,state_,action,action_,reward,done)
                self.actor.train(state,action,TD_error,done)
                single_returns+=(reward)
                state = state_
                if done:breakif history_returns:
                history_returns.append(history_returns[-1]*0.9+0.1*single_returns)else:
                history_returns.append( single_returns)
            self.logger.info("epoch:{}\{} || epoch return:{:,.4f} || history return:{:,.4f}".format(tran_epochs,epoch+1,single_returns,history_returns[-1]))
        self.env.close()

    def test(self,max_act=1000):
        state = self.env.reset()
        single_returns =0for iter inrange(max_act):
            self.env.render()
            action = self.actor.predict(state)
            state_, reward, done, info = self.env.step(action)
            single_returns +=(reward)if done:
                self.logger.info("End in {} iterations".format(iter+1))breakif not done:
            self.logger.info("success and return is {}".format(single_returns))if __name__ =='__main__':
    logger = logging.getLogger()
    logger.setLevel(logging.INFO)
    screen_handler = logging.StreamHandler(sys.stdout)
    screen_handler.setLevel(logging.INFO)
    formatter = logging.Formatter('%(asctime)s - %(module)s.%(funcName)s:%(lineno)d - %(levelname)s - %(message)s')
    screen_handler.setFormatter(formatter)
    logger.addHandler(screen_handler)

    agent =Agent(logger=logger)
    agent.train(tran_epochs=2000,max_act=500)
    agent.test()

本文部分内容为参考B站学习视频书写的笔记！

by CyrusMay 2022 03 29

摸不到的颜色 是否叫彩虹
看不到的拥抱 是否叫做微风
————五月天（星空）————