0
0

立体匹配入门指南（8）：视差图、深度图、点云

本篇是比较简单的基础概念，刚入门的朋友可能是需要的。
视差图三维点云
首先，我们要介绍下这三个概念。

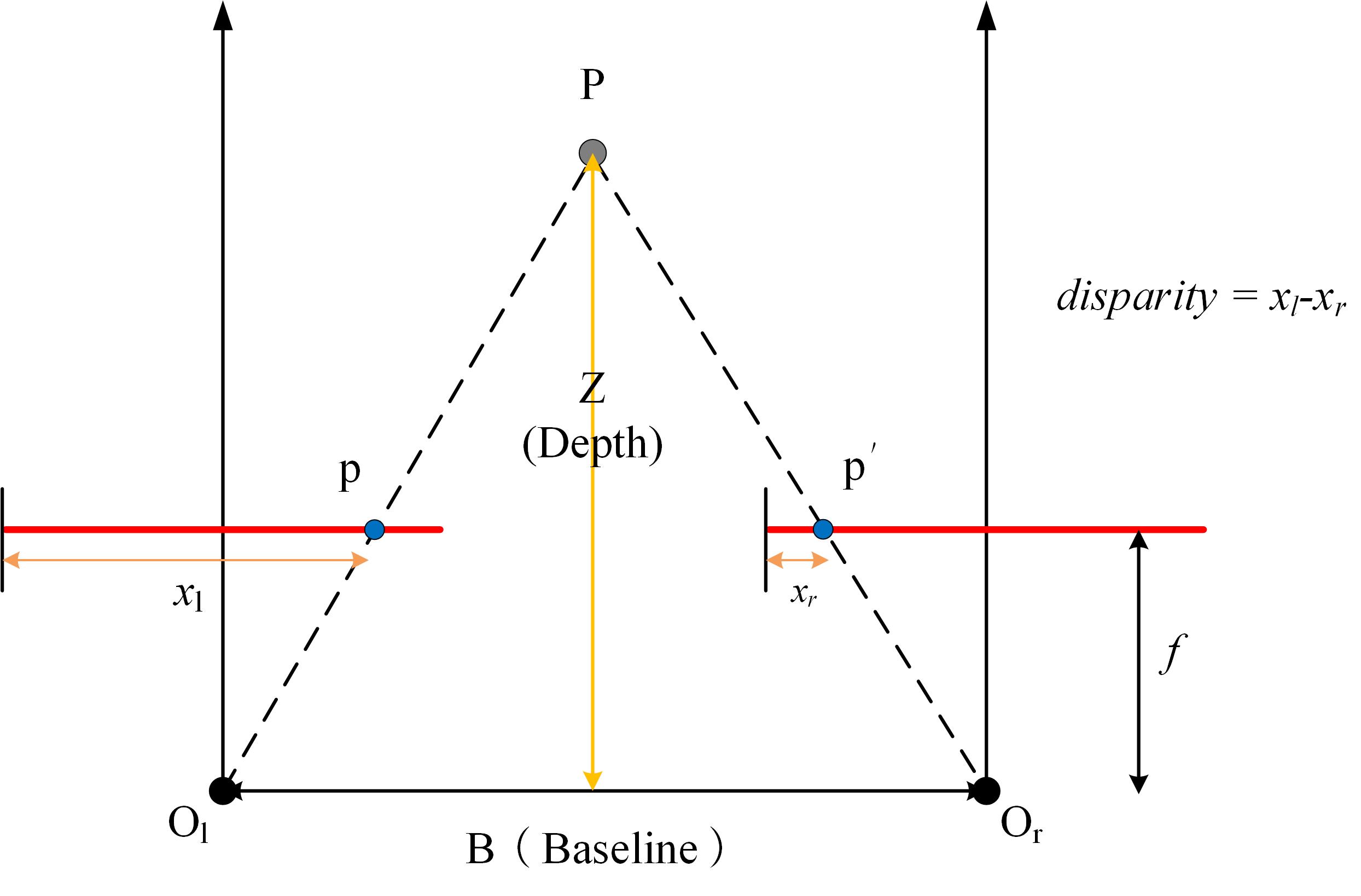
视差（disparity）

视差 

  1.     d
  2.    
  3.   
  4.   
  5.    d
  6.   
  7.  
  8. d 等于同名点对在左视图的列坐标减去在右视图上的列坐标，是**像素单位**
  10.  
  11.   
  12.    
  13.     
  14.      d
  15.     
  16.     
  17.      =
  18.     
  19.     
  20.      
  21.       x
  22.      
  23.      
  24.       l
  25.      
  26.     
  27.     
  28.      −
  29.     
  30.     
  31.      
  32.       x
  33.      
  34.      
  35.       r
  36.      
  37.     
  38.    
  39.    
  40.     d=x_l-x_r
  41.    
  42.   
  43.  d=xl​−xr​立体视觉里，视差概念在极线校正后的像对里使用。

深度（depth）

深度D等于像素在该视图相机坐标系下

  1.     Z
  2.    
  3.   
  4.   
  5.    Z
  6.   
  7.  
  8. Z坐标，是**空间单位**。深度并不特在校正后的图像对里使用，而是任意图像都可获取深度图。

视差图（disparity map）

视差图指存储立体校正后单视图所有像素视差值的二维图像。

  1. 视差图是一张二维图像，和原图等大小
  2. 视差图每个位置保存的以像素为单位的该位置像素的视差值
  3. 以左视图视差图为例，在像素位置p的视差值等于该像素在右图上的匹配点的列坐标减去其在左图上的列坐标

深度图（depth map）

深度图指存储单视图所有像素的深度值的二维图像，是空间单位，比如毫米。

  1. 深度图是一张二维图像，和原图等大小，也就和视差图等大小
  2. 深度图每个位置保存的是该位置像素的深度值
  3. 深度值就是相机坐标系下的Z坐标值

点云（point cloud）

点云指三维空间的三维点集合，坐标属性（

  1.     X
  2.    
  3.    
  4.     ,
  5.    
  6.    
  7.     Y
  8.    
  9.    
  10.     ,
  11.    
  12.    
  13.     Z
  14.    
  15.   
  16.   
  17.    X,Y,Z
  18.   
  19.  
  20. X,Y,Z），法线属性（
  22.  
  23.   
  24.    
  25.     
  26.      N
  27.     
  28.     
  29.      x
  30.     
  31.    
  32.    
  33.     ,
  34.    
  35.    
  36.     
  37.      N
  38.     
  39.     
  40.      y
  41.     
  42.    
  43.    
  44.     ,
  45.    
  46.    
  47.     
  48.      N
  49.     
  50.     
  51.      z
  52.     
  53.    
  54.   
  55.   
  56.    N_x,N_y,N_z
  57.   
  58.  
  59. Nx​,Ny​,Nz​）（可选），颜色属性（
  61.  
  62.   
  63.    
  64.     R
  65.    
  66.    
  67.     ,
  68.    
  69.    
  70.     G
  71.    
  72.    
  73.     ,
  74.    
  75.    
  76.     B
  77.    
  78.   
  79.   
  80.    R,G,B
  81.   
  82.  
  83. R,G,B）（可选）

其次，为什么会有视差图和深度图呢？

我们知道，立体匹配一般是指逐像素的稠密匹配，这意味着每个像素都会得到一个视差值（包括无效值），如何存储这些视差值呢，显然以二维图的方式存储是很合适的，最大的两点优势是一方面可以通过像素坐标快速的在二维图中找到对应位置的视差值，而且和图像一样是有序的，邻域检索、视差滤波等将会变得非常方便；另一方面是可以直观的通过观察视差图和原图的对比，对视差图的质量有初步的判定。

而深度图的意义则是以更少的存储空间、有序的表达图像匹配的三维成果。更少的存储空间是因为只保存了一个深度值，而不是三维点云的三个坐标值，而深度值是可以结合像素坐标计算三维点坐标值的。有序是因为深度图和原图像素是一一对应的，所以原图的邻域信息完全继承到了深度图里。

这就是视差图和深度图的意义，视差图是立体匹配算法的产出，而深度图则是立体匹配到点云生成的中间桥梁。

视差图和深度图中间，有着一对一的转换公式：

  1.      D
  2.     
  3.     
  4.      =
  5.     
  6.     
  7.      
  8.       
  9.        B
  10.       
  11.       
  12.        f
  13.       
  14.      
  15.      
  16.       
  17.        d
  18.       
  19.       
  20.        +
  21.       
  22.       
  23.        (
  24.       
  25.       
  26.        
  27.         x
  28.        
  29.        
  30.         
  31.          0
  32.         
  33.         
  34.          r
  35.         
  36.        
  37.       
  38.       
  39.        −
  40.       
  41.       
  42.        
  43.         x
  44.        
  45.        
  46.         
  47.          0
  48.         
  49.         
  50.          l
  51.         
  52.        
  53.       
  54.       
  55.        )
  56.       
  57.      
  58.     
  59.    
  60.    
  61.     D=\frac {Bf}{d+(x_{0r}-x_{0l})}
  62.    
  63.   
  64.  D=d+(x0r​−x0l​)Bf​

其中，

  1.     D
  2.    
  3.   
  4.   
  5.    D
  6.   
  7.  
  8. D为深度，
  10.  
  11.   
  12.    
  13.     d
  14.    
  15.   
  16.   
  17.    d
  18.   
  19.  
  20. d为视差，
  22.  
  23.   
  24.    
  25.     B
  26.    
  27.   
  28.   
  29.    B
  30.   
  31.  
  32. B为基线长度，
  34.  
  35.   
  36.    
  37.     f
  38.    
  39.   
  40.   
  41.    f
  42.   
  43.  
  44. f为焦距（像素单位），
  46.  
  47.   
  48.    
  49.     
  50.      x
  51.     
  52.     
  53.      
  54.       0
  55.      
  56.      
  57.       l
  58.      
  59.     
  60.    
  61.   
  62.   
  63.    x_{0l}
  64.   
  65.  
  66. x0l​和
  68.  
  69.   
  70.    
  71.     
  72.      x
  73.     
  74.     
  75.      
  76.       0
  77.      
  78.      
  79.       r
  80.      
  81.     
  82.    
  83.   
  84.   
  85.    x_{0r}
  86.   
  87.  
  88. x0r​分别为左右视图主点的列坐标。，另一个较为熟知的公式是
  90.  
  91.   
  92.    
  93.     
  94.      D
  95.     
  96.     
  97.      =
  98.     
  99.     
  100.      
  101.       
  102.        B
  103.       
  104.       
  105.        f
  106.       
  107.      
  108.      
  109.       d
  110.      
  111.     
  112.    
  113.    
  114.     D=\frac {Bf}{d}
  115.    
  116.   
  117.  D=dBf​

这是在左右视图主点的列坐标相同的特殊情况，比如主点都在中心。

深度图计算相机坐标系下的点云，也有着简单的公式：

  1.         Z
  2.        
  3.       
  4.      
  5.      
  6.       
  7.        
  8.         
  9.         
  10.          =
  11.         
  12.         
  13.          D
  14.         
  15.        
  16.       
  17.      
  18.     
  19.     
  20.      
  21.       
  22.        
  23.         X
  24.        
  25.       
  26.      
  27.      
  28.       
  29.        
  30.         
  31.         
  32.          =
  33.         
  34.         
  35.          
  36.           
  37.            D
  38.           
  39.           
  40.            (
  41.           
  42.           
  43.            x
  44.           
  45.           
  46.            −
  47.           
  48.           
  49.            
  50.             x
  51.            
  52.            
  53.             
  54.              0
  55.             
  56.             
  57.              l
  58.             
  59.            
  60.           
  61.           
  62.            )
  63.           
  64.          
  65.          
  66.           f
  67.          
  68.         
  69.        
  70.       
  71.      
  72.     
  73.     
  74.      
  75.       
  76.        
  77.         Y
  78.        
  79.       
  80.      
  81.      
  82.       
  83.        
  84.         
  85.         
  86.          =
  87.         
  88.         
  89.          
  90.           
  91.            D
  92.           
  93.           
  94.            (
  95.           
  96.           
  97.            y
  98.           
  99.           
  100.            −
  101.           
  102.           
  103.            
  104.             y
  105.            
  106.            
  107.             
  108.              0
  109.             
  110.             
  111.              l
  112.             
  113.            
  114.           
  115.           
  116.            )
  117.           
  118.          
  119.          
  120.           f
  121.          
  122.         
  123.        
  124.       
  125.      
  126.     
  127.    
  128.    
  129.     \begin{aligned} Z &= D\\ X &= \frac {D(x-x_{0l})}{f}\\ Y &= \frac {D(y-y_{0l})}{f} \end{aligned}
  130.    
  131.   
  132.  ZXY​=D=fD(x−x0l​)​=fD(y−y0l​)​​

其中，

  1.     x
  2.    
  3.    
  4.     ,
  5.    
  6.    
  7.     y
  8.    
  9.   
  10.   
  11.    x,y
  12.   
  13.  
  14. x,y为像素的列坐标和行坐标，
  16.  
  17.   
  18.    
  19.     
  20.      x
  21.     
  22.     
  23.      
  24.       0
  25.      
  26.      
  27.       l
  28.      
  29.     
  30.    
  31.   
  32.   
  33.    x_{0l}
  34.   
  35.  
  36. x0l​和
  38.  
  39.   
  40.    
  41.     
  42.      y
  43.     
  44.     
  45.      
  46.       0
  47.      
  48.      
  49.       l
  50.      
  51.     
  52.    
  53.   
  54.   
  55.    y_{0l}
  56.   
  57.  
  58. y0l​为主点的像素坐标。

常见问答：
问：为什么我从.png格式的视差图里读取到的视差值和真实值有很大差异？
答： 我们要先搞清楚，视差图是如何存储的。通常而言，我们是把二维视差图以图像格式存储，常见的格式有png、tif、pfm等，但这些图像格式存储的数据类型是有区别的，其中png只能存储整数，而tif和pfm则可以存储小数。而显然准确的视差值必然是浮点型的小数，所以存储为tif和pfm可以原值无损存储，而存储为png必然会损失精度，所以有的代码比如opencv会把得到的浮点型视差值乘以16倍取整，存储到png里，这样存储视差值的精度变为1/16，对于这种情况我们在读取png后要先除以16才是真实视差值，且视差会有阶梯分层现象。

那有同学就问，既然这样为什么要存储png呢？是因为目前主流的图像软件，不支持直接看浮点格式的tif和pfm，存储为png可以更好的观看视差图，当然要是实际生产使用，是必然不建议存储为png的，用来查看视差结果是可以的。

还有人会直接把视差值拉伸或者压缩到0~255，存储到png或bmp等存储整数的格式中，这样的视差图只能用来观看视差效果，没有其他作用，比如我的代码里的存储方式。

问：极线像对下的深度图和原图的深度图是一样的吗？如何转换？
答： 不一样，因为深度图是在视图所在的相机坐标系下的，所以和相机坐标系强挂钩，极限校正后的左视图和原始的左视图是不一样的相机坐标系，所以它们的深度图是不一样的。

  1. 对于极线像对左视图某像素 p p p，通过单应变换 H H H 转换到原左视图上，得到原图上的像素坐标 q q q。
  2. 将 p p p的相机坐标系坐标通过一个旋转 R R R 变换到原左视图的相机坐标系坐标，得到 q q q 的深度。
    1.                                H                              H                  H和                                   R                              R                  R在极线校正步骤可以获取（极线校正的必然产出）。
标签： 计算机视觉 人工智能 立体视觉
本文转载自: https://blog.csdn.net/rs_lys/article/details/125017920
版权归原作者 李迎松~ 所有， 如有侵权，请联系我们删除。
登录后发布评论

“立体匹配入门指南（8）：视差图、深度图、点云”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

网络安全法-网络运行安全

使用selenium/drissionpage时如何阻止chrome自动跳转http到https

docker desktop 里部署的Open WebUI 管理员密码忘记了的处理方法

在ubuntu20.04中搭建onsite比赛运行环境

利用开源的低代码表单设计器FcDesigner高效管理和渲染复杂表单结构

Kafka学习笔记

【前端】浏览器输入url到页面呈现发生了什么？

文章导航
没有找到文章内容分段。。。