都2022了，我不允许你还不懂快速排序 ＜快速排序算法＞【附动图详解~】【快排的三种版本~】【快排的优化】

写给前面：

💛生活的真谛从来都不在别处，就在日常一点一滴的奋斗里🧡

💚文章目录呀💚

💫快排思想💫

任取待排序元素序列中的某元素作为

基准值

，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于

基准值

，右子序列中所有元素均大于

基准值

，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止

听上去有些抽象？
实际上 这似乎和二叉树的前序遍历有些像~
先根，然后递归左，回来递归右

1️⃣hoare版本

📝步骤📝

1. 首先找一个基准值 key,一般我们找数组的最左或者最右边（以左边基准值为例）
2. 定义两个下标 left和right
3. right向左找比key小的数
4. left向右去找比key大的数
5. 二者交换，进行下一次寻找

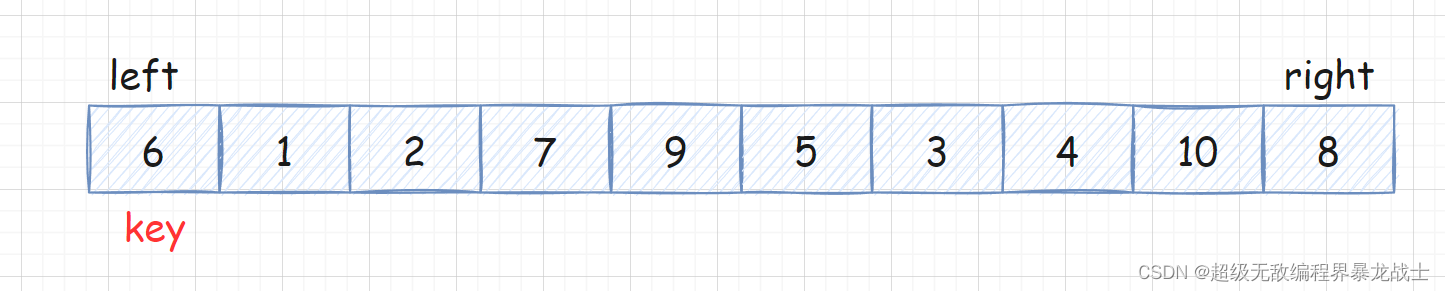
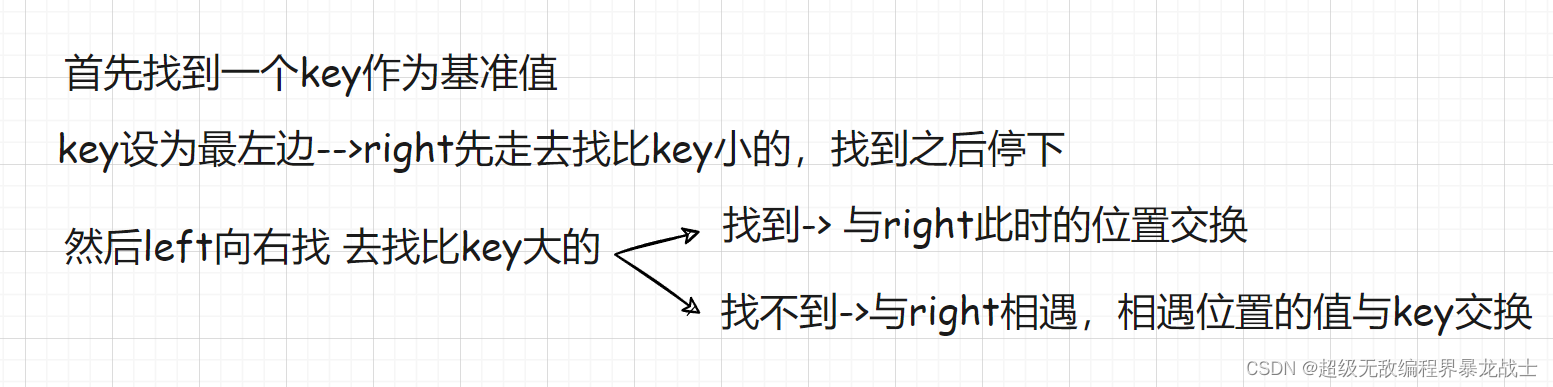
注意：

• 如果right向左找，一直找不到比key小的，说明key右边全部比key小
• left向右找，如果相遇，即left==right,此时的值一定比key小，因为right向左找到一个位置，这个位置一定是小于key right才会停下来等待left

🎥排序一趟动图演示🎥

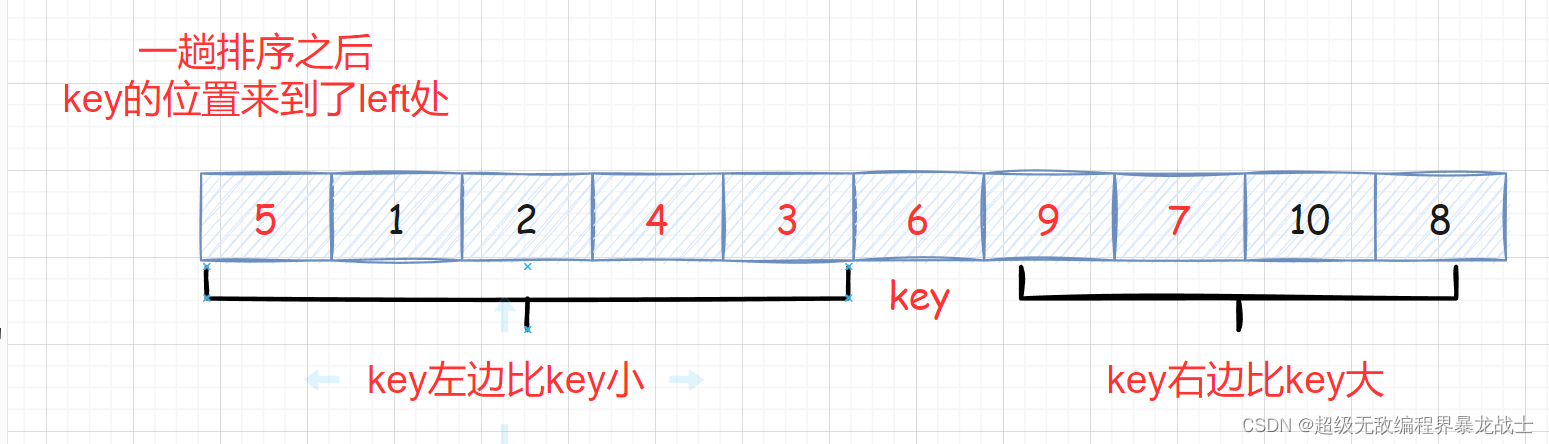
此时 相当于完成了局部的排序：左边都小于key 右边都大于key
此时 被分成了三部分

[begin,keyi-1]

,

keyi

,

[keyi+1,begin]

然后就去以相同的步骤重复

左子区间

和

右子区间

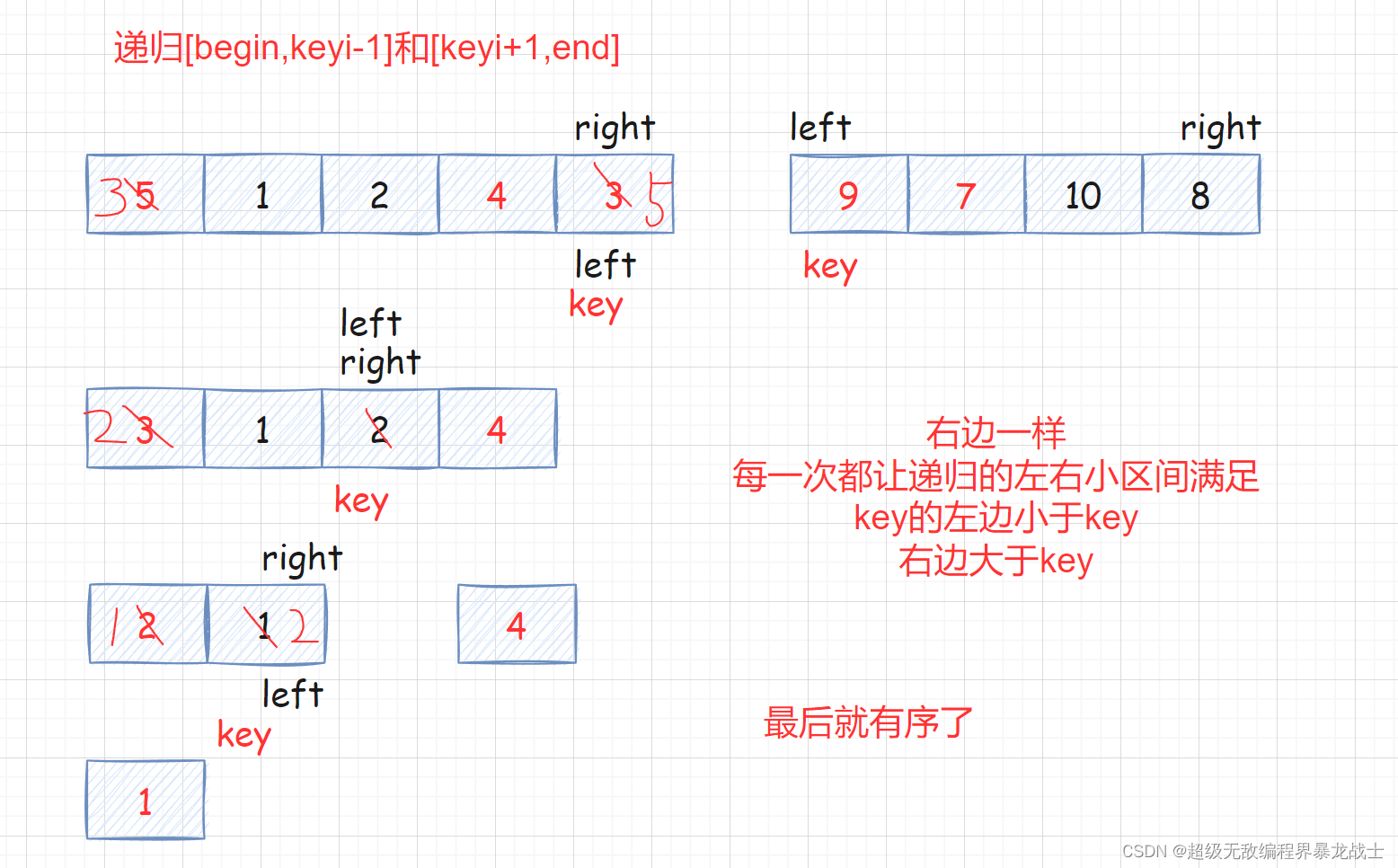
❗注意事项❗

1. 为什么key为最左边的时候，从右向左找？这里是hoare方法中比较别扭的地方****结论：因为要保证相遇的位置比key小，或者就是key的位置分析
2. 越界访问问题 解决方法：加一个条件left<right 同时这个条件也保证了：left和right不会错过，只要相等就会跳出

☃️完整代码☃️

// 霍尔版本voidQuickSort(int* a,int begin,int end){//递归的返回条件if(begin >= end){return;}int left = begin;int right = end;int keyi = left;while(left < right){//右边先走，找小while(left < right && a[right]>= a[keyi]){--right;}//左边走，找大while(left < right && a[left]<= a[keyi]){++left;}//找到交换Swap(&a[left],&a[right]);}//当left==right的时候，交换keyi和left的值Swap(&a[keyi],&a[left]);//更新keyi
    keyi = left;// [begin,keyi-1] keyi [keyi+1,end]//分治思想， 把keyi左右的序列都变成有序 整体就是有序了！QuickSort(a, begin, keyi -1);QuickSort(a, keyi +1, end);}

2️⃣填坑法

上面的hoare方法中存在一个问题：
我们如果选取最左边为key，需要

先从右边向左找小于key的值

同理，如果选取最右边为key，需要

先从左边向右找大于key的值

📝步骤📝

1. 首先将第一个数据放在临时变量key中，形成一个坑位
2. 右边去找小于key的值（因为左边有坑，哪边有坑，另一边就去找值去填坑）
3. 右边找到小于key的值，把值填入坑中，然后把该位置变成新的坑
4. 然后左边找大于key 的值，找到把值填入坑，改位置变成新的坑
5. 往复循环 (左右两个位置一定保持有一个是坑)
6. 最后相遇，把key填到坑的位置
7. 完成一趟排序，递归子区间[begin,pit-1],[pit+1,end]

🎥排序一趟动图演示🎥

填坑法的出现就是解决了 这个有点别扭的问题
哪里有坑，就从另一侧去找值 来天坑，更自然一些

但是 挖坑法单躺得到的顺序可能和hoare版本得到的不同

☃️完整代码☃️

// 填坑法voidQuickSort_pit(int* a,int begin,int end){if(begin >= end){return;}//拿出坑位元素int pit = begin;//假设初始坑位为最左侧int key = a[pit];int left = begin;int right = end;while(left < right){//右边去找小while(left < right && a[right]>= key){--right;}//右边找到小了，填坑,
        a[pit]= a[right];//同时right位置为新的坑，可以被任意填
        pit = right;//左边去找大while(left < right && a[left]<= key){++left;}//左边找到了，填坑
        a[pit]= a[left];//更新坑位
        pit = left;}//当left==right的时候//把key填入坑位
    a[pit]= key;//然后去递归 左右子区间//[begin,pit-1],pit,[pit+1,end]QuickSort_pit(a, begin, pit -1);QuickSort_pit(a, pit +1, end);}

挖坑法其实效率上并没有带来提升
只是相对于hoare方法好理解了一点点

但是有一类题喜欢考

选择题：给你一个数组，经过一趟快速排序，下列可能的结果有(不定项选择)
        这时候需要考虑到 hoare法和挖坑法了

3️⃣前后指针法

📝步骤📝

定义两个下标

prev

和

cur

还是假设 key为开头第一个元素

1. 最开始，prev指向序列开头，cur指向prev的下一个位置
2. cur去向后走去找小于key的数
3. 如果cur指向的数据小于key，那么prev先向后走一步，然后交换prev和cur指向的数据，然后cur下标向后走（cur++)
4. 如果cur指向的数据大于等于key，不做处理
5. 最后cur走完，就交换prev和key的值
6. 然后递归子区间 [begin,prev-1],[prev+1,end]

🎥排序一趟动图演示🎥

经过一次排序，

prev

前面的 都小于key，后面的都大于key

分析

为什么要这样做呢？

• 刚开始prev和cur是挨着的，cur是一直向后走的，如果cur指向的值大于key，那么cur直接++，这样prev和cur之间就是比key大的数
• 然后若cur遇到比key小的，就换到prev的后面
• 这样走完，cur的作用就是把前面的大与key的数换到后面去
• 最后prev一定是最后一个比key小的

注意：如果

cur

的下一个就是

prev

就不需要交换

所以

prev

的意思就是 大于key 的数据的前一个！

☃️完整代码☃️

voidQuickSort_prev(int* a,int begin,int end){if(begin >= end){return;}int keyi = begin;int prev = begin;//标记比key大的前一个位置int cur = begin +1;while(cur <= end){//如果cur小于key 并且cur与prev之间存在比key大的元素 那么prev的后一个与cur交换if(a[cur]< a[keyi]&&++prev < cur){Swap(&a[prev],&a[cur]);}++cur;}//最后交换prev与keyi位置 --keyi的位置变成了prevSwap(&a[prev],&a[keyi]);//此时 prev前面的都比key小 后面的都比key大//递归，[begin,keyi-1],keyi,[keyi+1,end]
    keyi = prev;QuickSort_prev(a, begin, keyi -1);QuickSort_prev(a, keyi +1, end);}

💫快排的优化

🔹三数取中优化

分析

思考一个问题
以上的三种快排的实现，每一趟都是O(N)
那么快排的效率与什么有关呢？ –

key

的选取

• 最好情况：每一次key都是中间的数，这样每一次都是二分，一共需要递归logN层 时间复杂度为O(N*logN）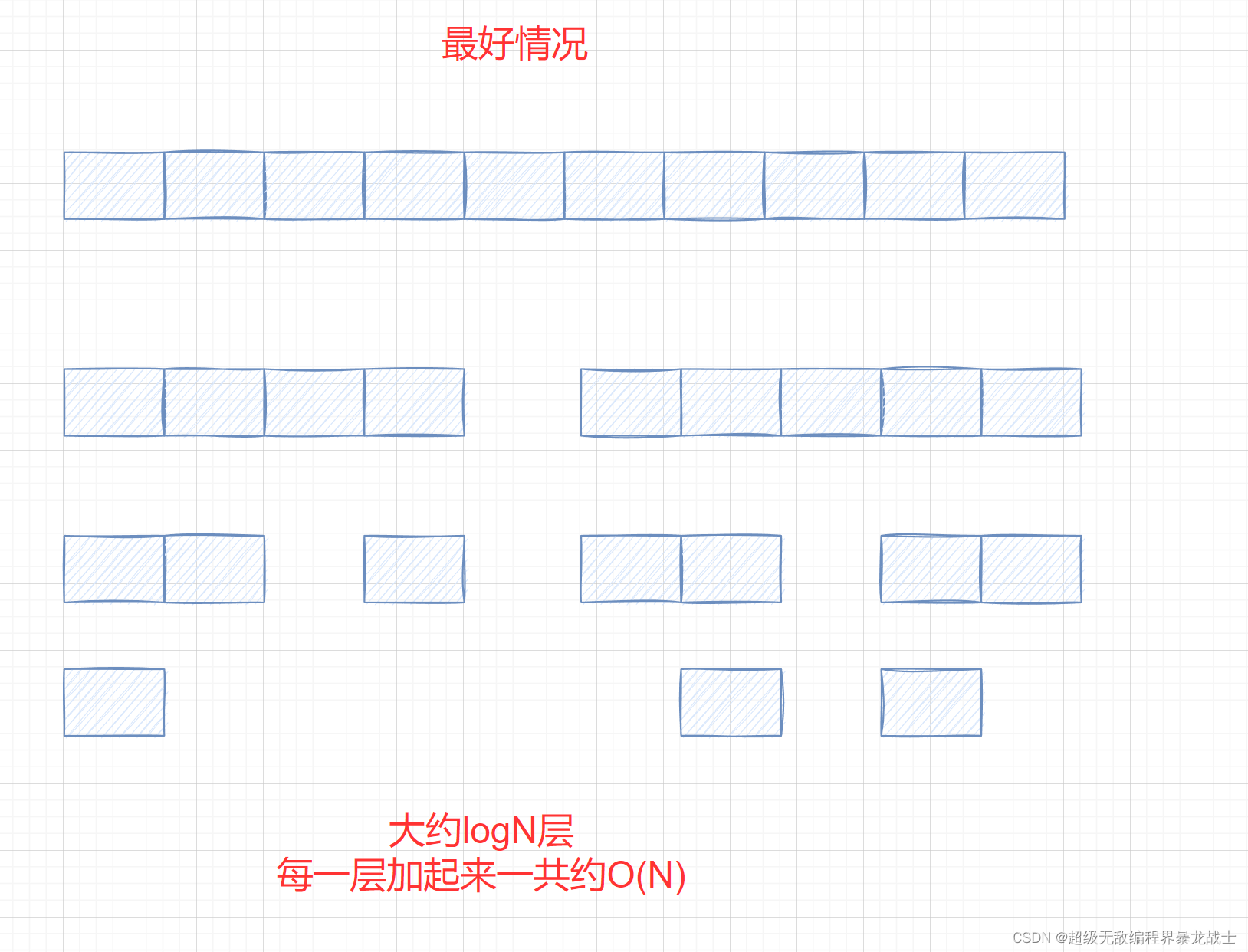
• 最坏情况：数组已经升序/降序或接近有序，这样每一次key都选的最大的 或者最小的，需递归N层，并且数据量较大的情况会发生栈溢出

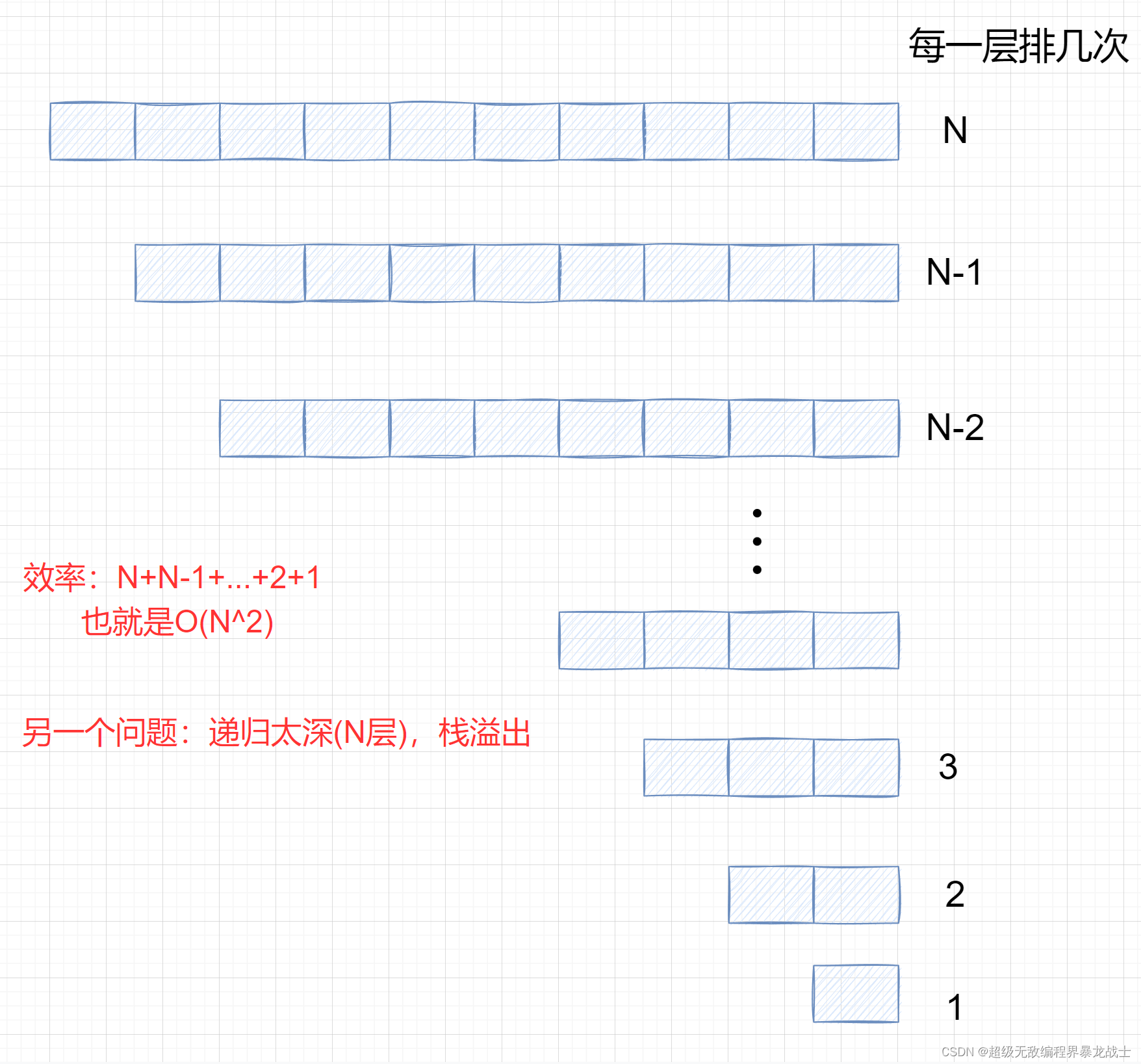
那么key如何选取，才能提高效率？
分析：如果是有序的情况下，一定是两端是最大或者最小
所以尽量选中间附近的

1. 随机选key
2. 三数取中法选key ：在第一个，中间，和最后一个之间选出不是最大也不是最小的那个数 （避免了最小值做key和最大值做key的情况）

我们选好key之后，还是把最左侧作为key（算法保持不变）
把选出的key与最左侧

begin

位置交换就可以了！

☃️完整代码☃️

//三数取中法intGetMidIndex(int* a,int begin,int end){int mid = begin +(end - begin)/2;//找出中间坐标if(a[begin]< a[mid]){if(a[mid]< a[end])//如果end最大{return mid;}elseif(a[begin]< a[end])//来到这说明mid最大，看begin和end{return end;}else{return begin;}}else//来到这说明begin>=mid{if(a[mid]>a[end])//说明begin最大 {return mid;}elseif(a[begin]>a[end])//来到这说明mid最小 看begin和end{return end;}else{return begin;}}}voidQuickSort_prev(int* a,int begin,int end){if(begin >= end){return;}int keyi = begin;int prev = begin;//标记比key大的前一个位置int cur = begin +1;//三数取中法优化int midi =GetMidIndex(a, begin, end);//找到midi下标Swap(&a[keyi],&a[midi]);//与key位置交换while(cur <= end){//如果cur小于key 并且cur与prev之间存在比key大的元素 那么prev的后一个与cur交换if(a[cur]< a[keyi]&&++prev < cur){Swap(&a[prev],&a[cur]);}++cur;}//最后交换prev与keyi位置 --keyi的位置变成了prevSwap(&a[prev],&a[keyi]);//此时 prev前面的都比key小 后面的都比key大//递归，[begin,keyi-1],keyi,[keyi+1,end]
    keyi = prev;QuickSort_prev(a, begin, keyi -1);QuickSort_prev(a, keyi +1, end);}

🔸小区间优化

分析

由于快速排序是递归实现，当递归的小区间小到一定程度的时候，如果还是继续进行递归，反而影响效率
比如：如果区间长度为10，递归次数约为

12

次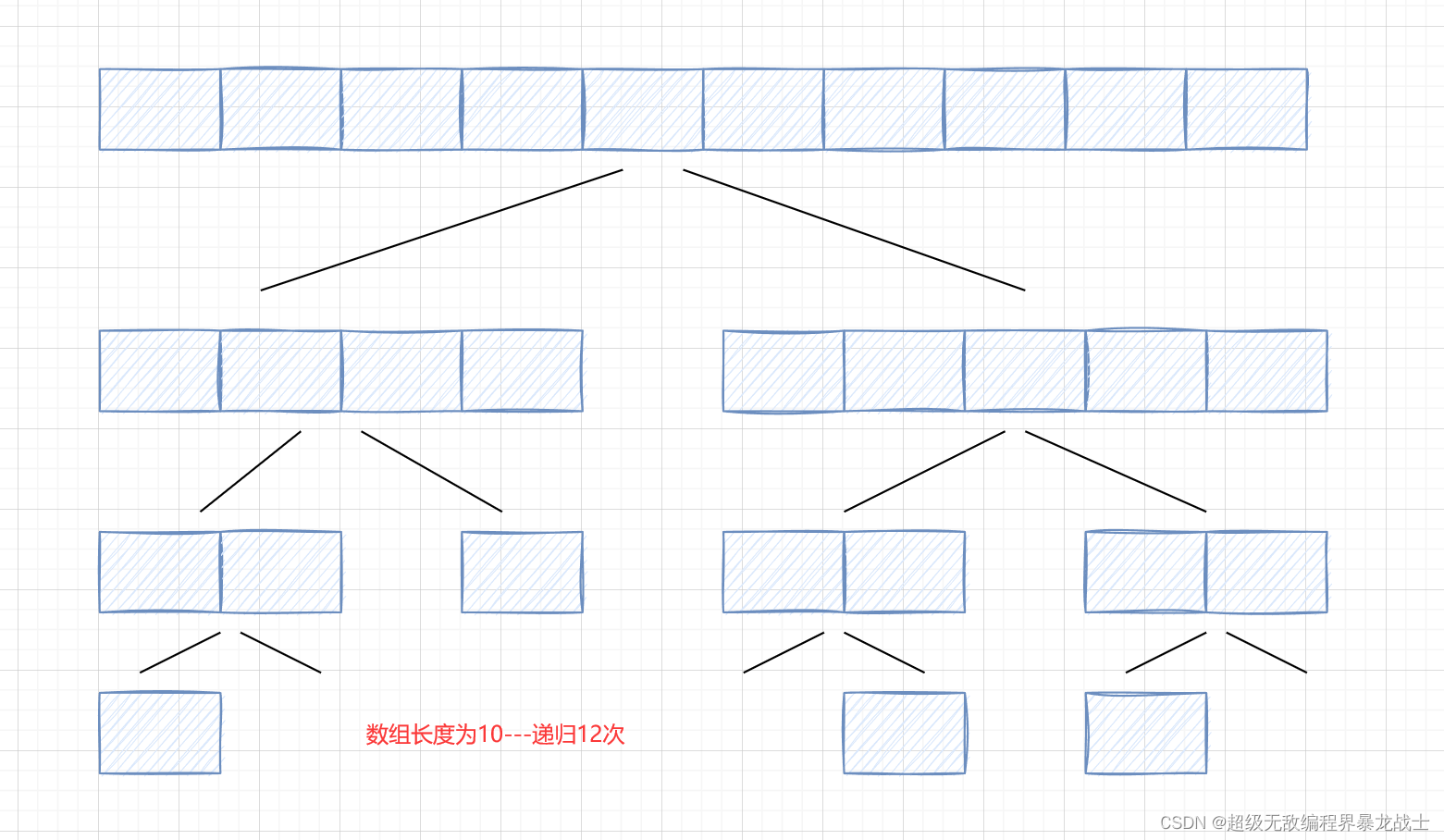

这时候，递归带来的消耗是大于直接对这些小区间进行排序的消耗的！所以当递归划分小区间的时候，区间比较小的时候，就不用递归去划分子区间了，可以考虑直接使用其他小排序对区间处理，一般使用简单排序中最优的----

插入排序

希尔、堆排等在数据量较大的时候才会有明显优势

注意：由于当前编译器对递归的优化已经挺高了，所以优化的效果没有特别特别明显，但是有一些优化的。

所以
如果假设区间小于10的时候，不再递归小区间，插入排序的消耗小于递归的消耗，将极大的优化整个排序

☃️完整代码☃️

voidQuickSort_prev(int* a,int begin,int end){if(begin >= end){return;}if(end - begin >10){int keyi = begin;int prev = begin;//标记比key大的前一个位置int cur = begin +1;//三数取中法优化int midi =GetMidIndex(a, begin, end);//找到midi下标Swap(&a[keyi],&a[midi]);//与key位置交换while(cur <= end){//如果cur小于key 并且cur与prev之间存在比key大的元素 那么prev的后一个与cur交换if(a[cur]< a[keyi]&&++prev < cur){Swap(&a[prev],&a[cur]);}++cur;}//最后交换prev与keyi位置 --keyi的位置变成了prevSwap(&a[prev],&a[keyi]);//此时 prev前面的都比key小 后面的都比key大//递归，[begin,keyi-1],keyi,[keyi+1,end]
        keyi = prev;QuickSort_prev(a, begin, keyi -1);QuickSort_prev(a, keyi +1, end);}else//如果区间小于10 进行插入排序{// 注意 数组是a+begin，a+begin是每一个小区间数组的开头// end-begin+1是小数组大小InsertSort(a + begin, end-begin+1);}}

插入排序如果忘了看这：插入排序

看一下小区间优化减少的递归次数
没优化：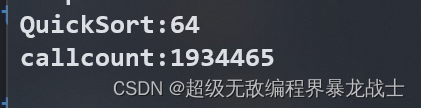

我们假设区间为<30的时候进行优化
优化了：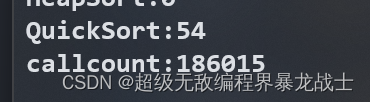

第一个是用时（ms)
第二个是调用次数
可以看到递归的调用次数 几乎减少了一个量级！！

🎯快排的非递归实现

递归的大问题：
极端场景下，递归层次太深，会出现栈溢出
因为栈很小

递归改成非递归的方法：

1. 直接改成循环 - - 如斐波那契数列
2. 用数据结构栈模拟递归过程（堆很大不怕溢出）

步骤：

1. 首先让begin和end入栈（end先入，begin后入）
2. 然后从栈中取出最上面两个元素，用left和right接受
3. 然后对[left,right]进行一趟快排
4. 然后分区间,[left,keyi-1],keyi,keyi+1,right]
5. 判断区间的长度是否为0，若大于0，依次把右子区间和左子区间入栈（注意栈的后进先出性质）
6. 下一次继续从栈中取出最上面两个元素，用left和right接收
7. 然后继续排序取出来的left和right区间
8. 继续分区间[left,keyi-1],keyi,keyi+1,right]

🎥动图演示出栈入栈过程🎥

☃️完整代码☃️

因为C中没有现成的写好的栈 所以还要自己写栈
如果忘了，戳这：数据结构-栈C实现

intPartSort3(int* a,int begin,int end){int keyi = begin;int prev = begin;//标记比key大的前一个位置int cur = begin +1;while(cur <= end){//如果cur小于key 并且cur与prev之间存在比key大的元素 那么prev的后一个与cur交换if(a[cur]< a[keyi]&&++prev < cur){Swap(&a[prev],&a[cur]);}++cur;}//最后交换prev与keyi位置 --keyi的位置变成了prevSwap(&a[prev],&a[keyi]);//此时 prev前面的都比key小 后面的都比key大//递归，[begin,keyi-1],keyi,[keyi+1,end]
    keyi = prev;return keyi;}//快排改成非递归voidQuickSortNore(int* a,int begin,int end){//创建一个栈
    ST st;StackInit(&st);//先把区间[begin,end]入栈StackPush(&st, end);StackPush(&st, begin);while(!StackEmpty(&st)){//每一次取出左右边界int left =StackTop(&st);StackPop(&st);int right =StackTop(&st);StackPop(&st);int keyi =PartSort3(a, left, right);//子区间[left,keyi-1],keyi,[keyi+1,right]//先入右子区间//判断一下 如果区间长度不为0才入栈if(keyi +1< right){StackPush(&st, right);StackPush(&st, keyi+1);}//左子区间if(left < keyi -1){StackPush(&st, keyi -1);StackPush(&st, left);}}//用完栈销毁StackDestory(&st);}

✨感谢阅读~ ✨
❤️码字不易，给个赞吧~❤️