点击上方“Deephub Imba”,关注公众号,好文章不错过 !
一般情况下的梯度提升实现(如 XGBoost)都使用静态学习率。但是我们可以使用一个函数,使函数参数可以作为训练时的超参数来确定训练时的“最佳”学习率形状。听着很拗口对吧,通俗的讲就是我们可以使用超参数来调整在整个训练过程的学习率计划。
Boosting 的简要回顾
对于Boosting 来说,最有名的就是 XGBoost了,它在 Kaggle 等平台上举办的众多数据科学竞赛中取得了巨大成功。在它成功以后,陆续还发布了几种变体例如 CatBoost 和 LightGBM。但是所有这些实现都基于 Friedman¹ 开发的梯度提升算法,该算法涉及迭代构建弱学习器(通常是决策树)的集合,其中每个后续学习器都针对前一个学习器的错误进行训练。让我们看一下统计学习元素²中算法的一些通用伪代码:

能够进行 boosting 的核心机制是收缩参数,这个参数它在每个 boosting 轮中惩罚每个学习者,通常称为“学习率”。它的主要功能是防止过度拟合,把它称作“学习率”是对梯度下降算法的一个很好的对应,并且启发了梯度提升的许多方面。为了利用学习率,Friedman 将 2.d 修改为:
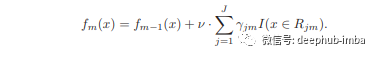
现在我们将每一轮的学习者乘以一个常数。但是我们应该使用什么常数呢?这个问题我们通常通过超参数调整来处理,我们会使用一个远低于 1 的数字,例如 0.1 或 0.01。通过这个数字为每一轮的结果设定一个惩罚值,使得该轮次的学习者得到的结果不会对前面轮次的结果产生过多的影响,但又会提高模型的效果。
使用动态学习率
既然这个常数被称作学习率,那么下一个自然而然的问题(尽管通常无关紧要)是为什么要使用常数?梯度下降具有允许学习率改变的动态策略。为什么梯度提升不能使用类似的想法?
嗯,好像是可以的……但是……这根本行不通。
通过查看文档和搜索引擎的结果显示,这个想法已经很早就被人测试过了,并且完成了一些利用衰减学习率的工作。例如该学习率开始时很大并且每轮都在缩小。但是在交叉验证中却看不到准确性的提高,而且在查看测试错误指标时,它的性能与使用常规固定数值方法之间的差异很小。这样的方法不起作用的原因似乎是个谜。
但是这也我们引向了 BetaBoost 的核心主题:我们可以在这方面做更多的研究。
Beta 密度函数
为了与我们的主题保持一致,我们进行了研究,并发现了一个看起来很有希望的函数:beta 函数。更具体地说就是beta 概率分布函数。
beta PDF是一个主要由 2 个参数描述的概率分布:α 和 β。除了这些参数之外,还有一些不太重要的参数。出于我们在很大程度上不关心函数作为概率密度函数的任何属性,只关心它对于boosting的结果,所以这里就不详细说明了。
Beta PDF 与许多其他函数相比的一个明显优势是可以使用它来实现各种形状³:
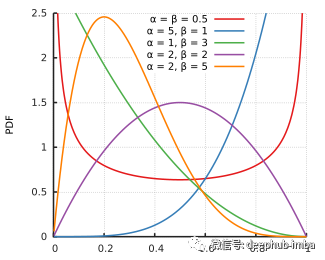
如果我们想做一些类似指数衰减的事情,或者在中间制造一个大的尖峰,只需要改变beta函数的参数就可以了。这意味着,如果我们将整个过程交给Hyperopt等超参数调优包,就可以自动发现“最适合”我们的数据的学习率形状。
虽然我也不知道为什么这些会带来好处,但是在这一领域可以做更多的研究。
BetaBoosting
这一切都将我们带到了 BetaBoosting。这不是构建树或提出拆分的新方法。它只是使用 XGBoost 学习 API 中的回调在每个训练轮次分配不同的学习率。我们的具体实现基于 Beta PDf 分配学习率——因此我们得到了名称“BetaBoosting”。
代码可通过 pip 安装以方便使用,并且需要 xgboost==1.5:
pip install BetaBoost==0.0.5
如前所述beta函数能生成各种形状。让我们看一下使用类默认参数的 BetaBoost。此函数将默认参数以及一些额外的配置传递给 scipy Beta PDF 函数:
def beta_pdf(scalar=1.5,
a=26,
b=1,
scale=80,
loc=-68,
floor=0.01,
n_boosting_rounds=100):
"""
Get the learning rate from the beta PDF
Returns
-------
lrs : list
the resulting learning rates to use.
"""
lrs = [scalar*beta.pdf(i,
a=a,
b=b,
scale=scale,
loc=loc)
+ floor for i in range(n_boosting_rounds)]
return lrs
这里是直接使用 BetaBoost 类:
from BetaBoost import BetaBoost as bb
import matplotlib.pyplot as plt
booster = bb.BetaBoost(n_boosting_rounds=100)
plt.plot(booster.beta_kernel())
plt.show()
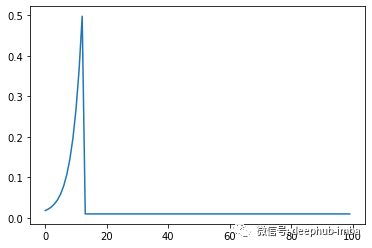
这种学习率的形状效果很好,这表明,在树的成长过程的中间阶段采取了更大的步骤,并且为我们提供最大的收益。
为了进一步研究,我们用模拟的数据运行它,并与其他学习速率进行比较。
首先,我们将导入并模拟一些数据:
progress1 = dict()
model1 = xgb.train(
maximize=True,
params=PARAMS,
dtrain=dtrain,
num_boost_round=max_iter,
early_stopping_rounds=max_iter,
evals=[(dtrain, 'train'),(dtest, 'test')],
evals_result=progress1,
verbose_eval=False,
callbacks=[xgb.callback.LearningRateScheduler(eta_decay)]
)
现在,我们使用常见的学习率0.01:
progress2 = dict()
model2 = xgb.train(
maximize=True,
params=PARAMS,
dtrain=dtrain,
num_boost_round=max_iter,
early_stopping_rounds=max_iter,
evals=[(dtrain, 'train'),(dtest, 'test')],
evals_result=progress2,
verbose_eval=False,
callbacks=[xgb.callback.LearningRateScheduler(list(np.ones(max_iter)*0.01))]
)
另外一个是0.1
progress3 = dict()
model3 = xgb.train(
maximize=True,
params=PARAMS,
dtrain=dtrain,
num_boost_round=max_iter,
early_stopping_rounds=max_iter,
evals=[(dtrain, 'train'),(dtest, 'test')],
evals_result=progress3,
verbose_eval=False,
callbacks=[xgb.callback.LearningRateScheduler(list(np.ones(max_iter)*0.1))]
)
最后,我们的BetaBoost,其中的fit方法返回与XGBoost中的train方法相同的输出
#Here we call the BetaBoost, the wrapper parameters are passed in the class init
bb_evals = dict()
from BetaBoost import BetaBoost as bb
betabooster = bb.BetaBoost(n_boosting_rounds=max_iter)
betabooster.fit(dtrain=dtrain,
maximize=True,
params=PARAMS,
early_stopping_rounds=max_iter,
evals=[(dtrain, 'train'),(dtest, 'test')],
evals_result=bb_evals,
verbose_eval=False)
让我们来看看每一轮测试准确性的结果:
plt.plot(progress1['test']['rmse'], linestyle = 'dashed', color = 'b', label = 'eta test decay')
plt.plot(progress2['test']['rmse'], linestyle = 'dashed', color = 'r', label = '0.01 test')
plt.plot(progress3['test']['rmse'], linestyle = 'dashed', color = 'black', label = '0.1 test')
plt.plot(bb_evals['test']['rmse'], linestyle = 'dashed', color = 'y', label = 'bb test')
plt.legend()
plt.show()
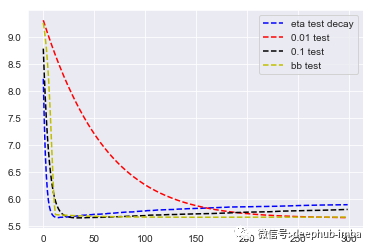
我们看到衰减的学习率实际上达到错误的最小值最快,但它也是一个不稳定的结果,因为它很快开始过度拟合了。接下来是 betaboosting 。与衰减测试集不同,我们可以看到它在收敛时还会继续缓慢地减少误差。最终在迭代 300 轮左右,它遇到了对应于恒定 0.01 学习率的错误率。所以看起来我们在这里得到了两全其美:我们很快收敛到接近最佳的测试准确度,然后我们可以抵抗过度拟合。但是,它真的表现最好吗?其实并不是
在最后的 100 次迭代中,0.01 略胜一筹。但是情况并非总是如此,我们将在下一篇文章中看到一些 使用5折CV 结果,其中优化的 BetaBooster 实际上在现实世界数据上的表现要优于优化的传统XGBoost
总结
使用 Beta 密度函数的梯度提升,它的学习率似乎为我们提供了更快的收敛和对过度拟合的健壮性。这样做的代价是要调整更多参数。此外,XGBoost 和 LightGBM都提供了回调函数可以动态的调整学习率。
最后如果要总结BetaBoosting它提供了更好的功能吗?
我们的回答是……
不敢保证,并且在这方面应该做更多的研究。
betaBoost的代码:https://github.com/tblume1992/BetaBoost
引用
- Friedman, J. H. “Stochastic Gradient Boosting.” (March 1999)
- Hastie, T., Tibshirani, R., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction. 2nd ed. New York: Springer.
- https://en.wikipedia.org/wiki/Beta_distribution
作者:Tyler Blume