动态系统建模-状态空间方程
状态空间方程是现代控制理论的基础, 它以矩阵的形式表达系统状态变量、 输入及输出之间的关系。 它可以描述和处理多输入多输出(MultipleInput Multiple Output, MIMO) 的系统。
状态空间方程
单输入单输出(SingleInput Single Output,SISO) 系统
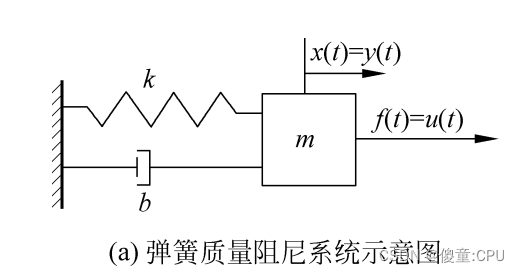
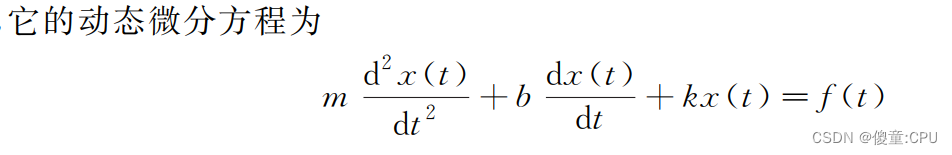
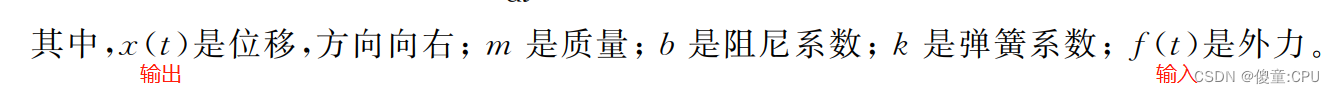
拉普拉斯变换后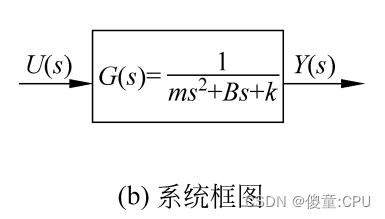
状态空间方程是一个集合, 它包含了系统的输入、 输出及状态变量, 并把它们用一系列的一阶微分方程表达出来。
对于本例中的二阶系统, 为了将其写成状态空间方程, 需要选取合适的状态变量(State Variables) , 才能使二阶系统转化为一系列的一阶系统。
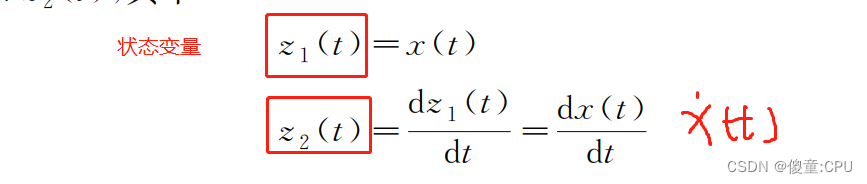
求状态变量的倒数。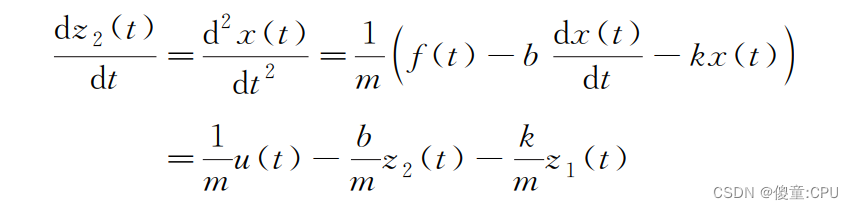
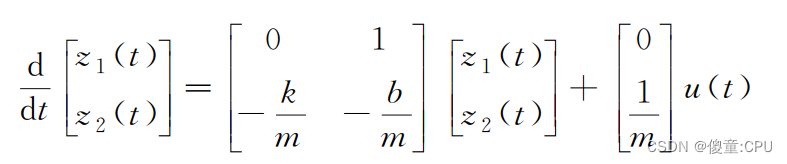
具体的推导过程
这说明, 当使用状态空间方程来描述系统时, 有n 个状态变量、m 个输出和p 个输入。它可以表达多状态、 多输出、 多输入的系统。 其中, 矩阵A 是n ×n 矩阵, 表示系统状态变量之间的关系, 称为状态矩阵或者系统矩阵。 矩阵B 是n ×p 矩阵, 表示输入对状态变量的影响, 称为输入矩阵或者控制矩阵。 矩阵C 是m ×n 矩阵, 表示系统的输出与系统状态变量之间的关系, 称为输出矩阵。 矩阵D 是m ×p 矩阵, 表示系统的输入直接作用在系统输出的部分, 称为直接传递矩阵。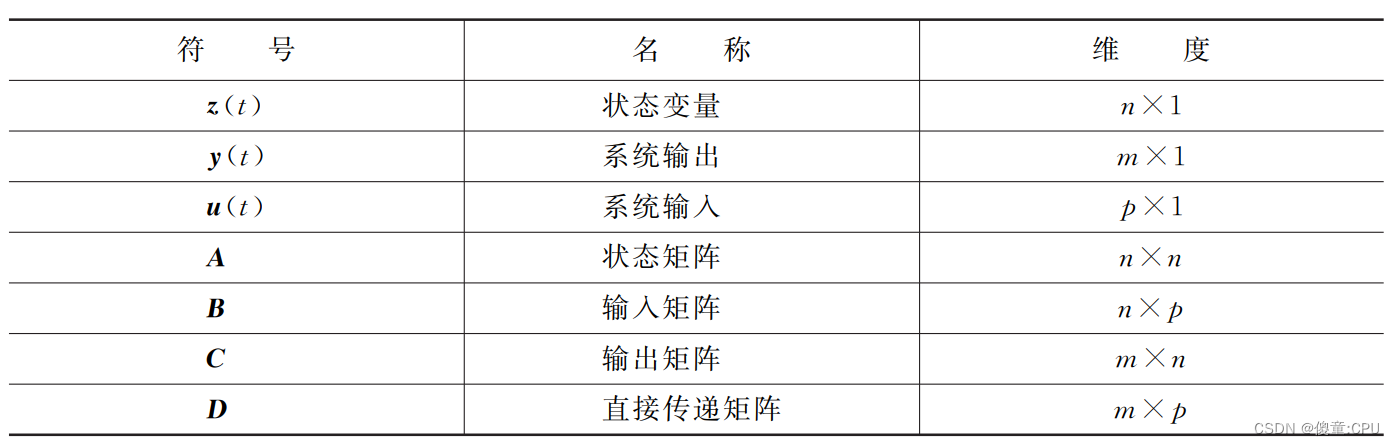
多输入多输出(MultipleInputs Multiple Outputs, MIMO) 系统
若要建立上述系统的状态空间方程, 首先要掌握它的动态微分方程。 这个系统可以考虑成两个闭合回路, 在每一个闭合回路里面使用基尔霍夫电压定律。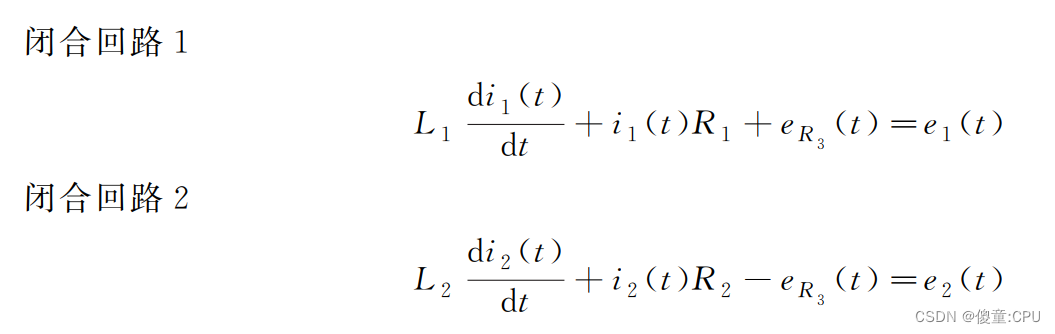
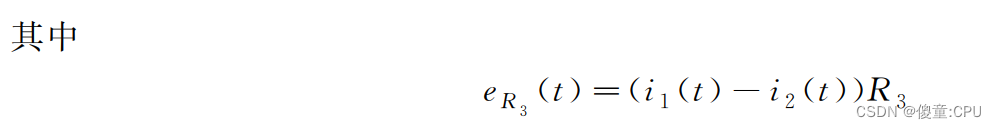
整理得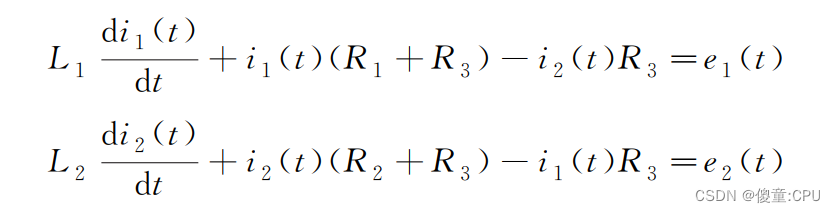
要消去谁的二阶导（或者存在一阶导的关系式），就令谁为状态变量。
求状态变量的倒数。
写成矩阵的形式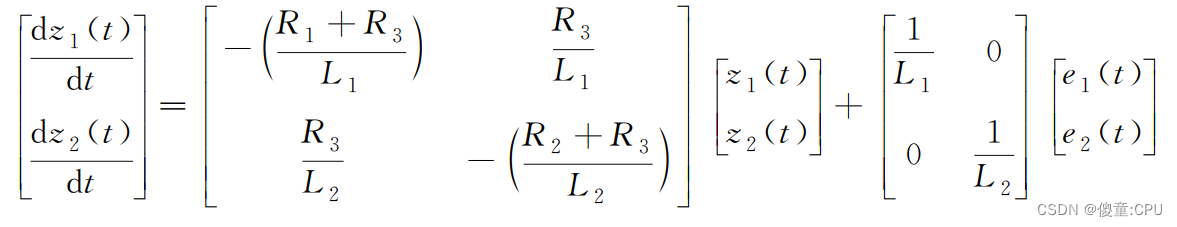
系统的状态空间方程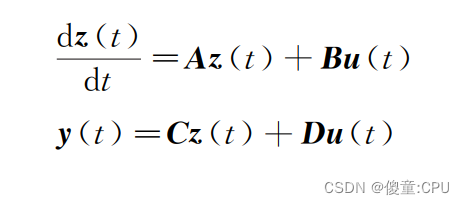
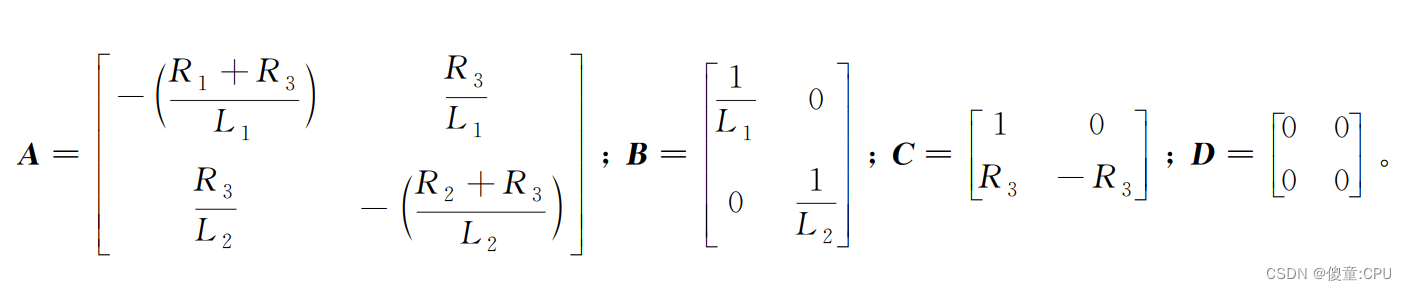
具体的推导过程。
状态方程与传递函数的关系
本文转载自: https://blog.csdn.net/qq_45159887/article/details/127082870
版权归原作者 傻童:CPU 所有， 如有侵权，请联系我们删除。
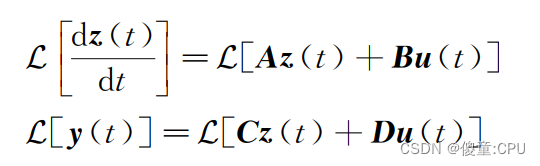
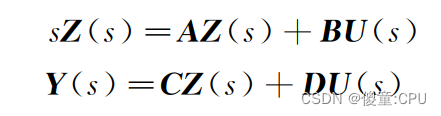
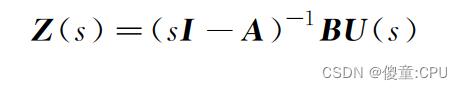
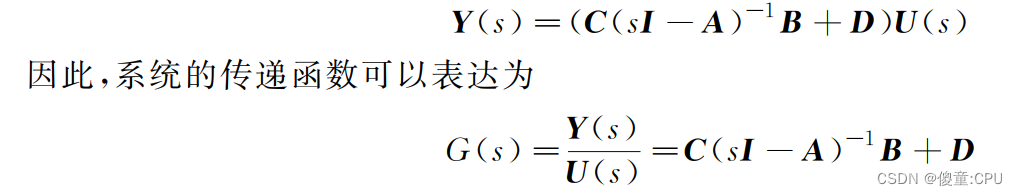
版权归原作者 傻童:CPU 所有， 如有侵权，请联系我们删除。