机器学习中的数学——距离定义（二）：曼哈顿距离（Manhattan Distance）

分类目录：《机器学习中的数学》总目录
相关文章：
· 距离定义：基础知识
· 距离定义（一）：欧几里得距离（Euclidean Distance）
· 距离定义（二）：曼哈顿距离（Manhattan Distance）
· 距离定义（三）：闵可夫斯基距离（Minkowski Distance）
· 距离定义（四）：切比雪夫距离（Chebyshev Distance）
· 距离定义（五）：标准化的欧几里得距离（Standardized Euclidean Distance）
· 距离定义（六）：马氏距离（Mahalanobis Distance）
· 距离定义（七）：兰氏距离（Lance and Williams Distance）/堪培拉距离（Canberra Distance）
· 距离定义（八）：余弦距离（Cosine Distance）
· 距离定义（九）：测地距离（Geodesic Distance）
· 距离定义（十）： 布雷柯蒂斯距离（Bray Curtis Distance）
· 距离定义（十一）：汉明距离（Hamming Distance）
· 距离定义（十二）：编辑距离（Edit Distance，Levenshtein Distance）
· 距离定义（十三）：杰卡德距离（Jaccard Distance）和杰卡德相似系数（Jaccard Similarity Coefficient）
· 距离定义（十四）：Ochiia系数（Ochiia Coefficient）
· 距离定义（十五）：Dice系数（Dice Coefficient）
· 距离定义（十六）：豪斯多夫距离（Hausdorff Distance）
· 距离定义（十七）：皮尔逊相关系数（Pearson Correlation）
· 距离定义（十八）：卡方距离（Chi-square Measure）
· 距离定义（十九）：交叉熵（Cross Entropy）
· 距离定义（二十）：相对熵（Relative Entropy）/KL散度（Kullback-Leibler Divergence）
· 距离定义（二十一）：JS散度（Jensen–Shannon Divergence）
· 距离定义（二十二）：海林格距离（Hellinger Distance）
· 距离定义（二十三）：α-散度（α-Divergence）
· 距离定义（二十四）：F-散度（F-Divergence）
· 距离定义（二十五）：布雷格曼散度（Bregman Divergence）
· 距离定义（二十六）：Wasserstein距离（Wasserstei Distance）/EM距离（Earth-Mover Distance）
· 距离定义（二十七）：巴氏距离（Bhattacharyya Distance）
· 距离定义（二十八）：最大均值差异（Maximum Mean Discrepancy, MMD）
· 距离定义（二十九）：点间互信息（Pointwise Mutual Information, PMI）

曼哈顿距离是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

下图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。

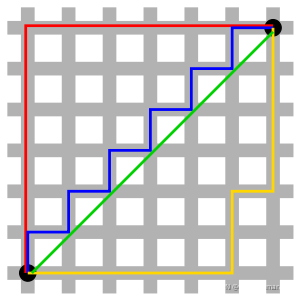
曼哈顿距离在2维平面是两点在纵轴上的距离加上在横轴上的距离，即：

     d
    
    
     (
    
    
     x
    
    
     ,
    
    
     y
    
    
     )
    
    
     =
    
    
     ∣
    
    
     
      x
     
     
      1
     
    
    
     −
    
    
     
      y
     
     
      1
     
    
    
     ∣
    
    
     +
    
    
     ∣
    
    
     
      x
     
     
      2
     
    
    
     −
    
    
     
      y
     
     
      2
     
    
    
     ∣
    
   
   
    d(x, y)=|x_1-y_1|+|x_2-y_2|
   
  
 d(x,y)=∣x1​−y1​∣+∣x2​−y2​∣

对于一个具有正南正北、正东正西方向规则布局的城镇街道（如：曼哈顿），从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。曼哈顿距离不是距离不变量，当坐标轴变动时，点间的距离就会不同。曼哈顿距离示意图在早期的计算机图形学中，屏幕是由像素构成，是整数，点的坐标也一般是整数，原因是浮点运算很昂贵，很慢而且有误差，如果直接使用AB的欧氏距离（欧几里德距离：在二维和三维空间中的欧氏距离的就是两点之间的距离），则必须要进行浮点运算，如果使用AC和CB，则只要计算加减法即可，这就大大提高了运算速度，而且不管累计运算多少次，都不会有误差。

    n
   
  
  
   n
  
 
n维空间中的欧几里得距离：

 
  
   
    
     d
    
    
     (
    
    
     x
    
    
     ,
    
    
     y
    
    
     )
    
    
     =
    
    
     
      ∑
     
     
      
       i
      
      
       =
      
      
       1
      
     
     
      n
     
    
    
     ∣
    
    
     
      x
     
     
      i
     
    
    
     −
    
    
     
      y
     
     
      i
     
    
    
     ∣
    
   
   
    d(x, y)=\sum_{i=1}^n|x_i-y_i|
   
  
 d(x,y)=i=1∑n​∣xi​−yi​∣

下面我们来看一下曼哈顿距离的Python实现：

defManhattanDistance(x, y):import numpy as np
    x = np.array(x)
    y = np.array(y)return np.sum(np.abs(x-y))