智能优化算法:北方苍鹰优化算法
文章目录
1.北方苍鹰优化算法简介
北方苍鹰优化算法(Northern Goshawk Optimization,NGO)是2022年由MOHAMMAD DEHGHANI等人提出的,该算法模拟了北方苍鹰在捕猎过程中的行为,具体包括猎物识别与攻击、追逐及逃生等行为。
2.北方苍鹰优化算法基本原理
2.1灵感来源和北方苍鹰的行为
北方苍鹰是鹰科的一个中大型猛禽,它首次被现在的学名,即苍鹰加以描述是林奈于1978年在他的自然系统中完成的。北方苍鹰是鹰属的一员,它捕猎各种猎物,包括小型和大型的鸟类以及其他鸟类,小型哺乳动物如老鼠、兔子、松鼠,甚至于狐狸和浣熊等动物。北方苍鹰是鹰属中唯一分布在欧亚大陆和北美的成员。雄性比雌性稍大一些。雄性的体长为46-61厘米,两翼之间的距离为89-105厘米,重约780克。然而,雌性物种长58-69厘米,体重1220克,两个翅膀之间的距离估计为108-127厘米。北方苍鹰的捕猎策略包括两个阶段:在第一阶段,在识别出猎物后,它以高速向猎物移动攻击;在第二阶段,在追逐猎取猎物。
2.2算法的数学模型
在北方苍鹰优化算法中,北方苍鹰捕猎过程分为两个阶段:猎物识别与攻击(勘探阶段),追逐及逃生(开发阶段)。
2.2.1 初始化
在北方苍鹰优化算法中,北方苍鹰种群可以用以下种群矩阵表示:
X
=
[
X
1
⋮
X
i
⋮
X
N
]
N
×
m
=
[
x
1
,
1
⋯
x
1
,
j
⋯
x
1
,
m
⋮
⋱
⋮
⋮
x
i
,
1
⋯
x
i
,
j
⋯
x
i
,
m
⋮
⋮
⋱
⋮
x
N
,
1
⋯
x
N
,
j
⋯
x
N
,
m
]
N
×
m
(1)
X=\left[\begin{array}{c} X_{1} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N} \end{array}\right]_{N \times m}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & \ddots & \vdots & & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & & \vdots & \ddots & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m} \tag{1}
X=X1⋮Xi⋮XNN×m=x1,1⋮xi,1⋮xN,1⋯⋱⋯⋯x1,j⋮xi,j⋮xN,j⋯⋯⋱⋯x1,m⋮xi,m⋮xN,mN×m(1)
式中:
X
X
X为北方苍鹰的种群矩阵;
X
i
X_i
Xi为第*i*个北方苍鹰的位置;为
x
i
,
j
x_{i,j}
xi,j第*i*个北方苍鹰的第*j*维的位置;N为北方苍鹰的种群数量;m为求解问题的维度。
在北方苍鹰优化算法中,求解问题的目标函数可以用来计算北方苍鹰的目标函数值;北方苍鹰种群的目标函数值可以用目标函数值向量表示:
F
=
[
F
1
⋮
F
i
⋮
F
N
]
N
×
1
=
[
F
(
X
1
)
⋮
F
(
X
i
)
⋮
F
(
X
N
)
]
N
×
1
(2)
F=\left[\begin{array}{c} F_{1} \\ \vdots \\ F_{i} \\ \vdots \\ F_{N} \end{array}\right]_{N \times 1}=\left[\begin{array}{c} F\left(X_{1}\right) \\ \vdots \\ F\left(X_{i}\right) \\ \vdots \\ F\left(X_{N}\right) \end{array}\right]_{N \times 1} \tag{2}
F=F1⋮Fi⋮FNN×1=F(X1)⋮F(Xi)⋮F(XN)N×1(2)
式中:
F
F
F为北 方苍鹰种群的目标函数向量;
F
i
F_i
Fi为第*i*个北方苍鹰的目标函数值。
2.2.2 第一阶段:猎物识别(勘探阶段)
北方苍鹰在捕猎的第一阶段,随机选择一个猎物,然后迅速攻击它。由于在搜索空间中对猎物的选择是随机的,因此这一阶段增加了NGO算法的勘探能力。这个阶段对搜索空间进行全局搜索,目的是确定最优区域。在这一阶段,北方苍鹰进行猎物选择和攻击的行为,用公式(3)~(5)描述:
P
i
=
X
k
,
i
=
1
,
2
,
…
,
N
,
k
=
1
,
2
,
…
,
i
−
1
,
i
+
1
,
…
,
N
(3)
{P_i} = {X_k},i = 1,2, \ldots ,N,k = 1,2, \ldots ,i - 1,i + 1, \ldots ,N \tag{3}
Pi=Xk,i=1,2,…,N,k=1,2,…,i−1,i+1,…,N(3)
x
i
,
j
n
e
w
,
P
1
=
{
x
i
,
j
+
r
(
p
i
,
j
−
I
x
i
,
j
)
,
F
P
i
<
F
i
x
i
,
j
+
r
(
x
i
,
j
−
p
i
,
j
)
,
F
P
i
≥
F
i
.
(4)
x_{i,j}^{new,P1} = {\begin{cases}{}{{x_{i,j}} + r\left( {{p_{i,j}} - I{x_{i,j}}} \right),}&{{F_{{P_i}}} < {F_i}}\\{{x_{i,j}} + r\left( {{x_{i,j}} - {p_{i,j}}} \right),}&{{F_{{P_i}}} \ge {F_i}}\end{cases}} . \tag{4}
xi,jnew,P1={xi,j+r(pi,j−Ixi,j),xi,j+r(xi,j−pi,j),FPi<FiFPi≥Fi.(4)
X
i
=
{
X
i
n
e
w
,
P
1
,
F
i
n
e
w
,
P
1
<
F
i
X
i
,
F
i
n
e
w
,
P
1
≥
F
i
(5)
{X_i} = {\begin{cases}{} {X_i^{new,P1},}&{F_i^{new,P1} < {F_i}}\\ {{X_i},}&{F_i^{new,P1} \ge {F_i}} \end{cases}} \tag{5}
Xi={Xinew,P1,Xi,Finew,P1<FiFinew,P1≥Fi(5)
式中:
P
i
P_i
Pi为第*i*个北方苍鹰的猎物的位置;
F
P
i
F_{Pi}
FPi为第*i*个北方苍鹰的猎物的位置的目标函数值;*k*是[1,*N*]范围内的随机整数;
X
i
n
e
w
,
P
1
X_i^{new,P1}
Xinew,P1为第*i*个北方苍鹰的新位置;
x
i
,
j
n
e
w
,
P
1
x_{i,j}^{new,P1}
xi,jnew,P1为第*i*个北方苍鹰的第*j*维的新位置;
F
i
n
e
w
,
P
1
F_i^{new,P1}
Finew,P1为基于第1阶段更新后第*i*个北方苍鹰的目标函数值;*r*是[0,1]范围内的随机数;
I
I
I为1或2的随机整数。
2.2.3 第二阶段:追逐及逃生(开发阶段)
在北方苍鹰攻击猎物后,猎物会试图逃跑。因此,在追逐猎物的收尾过程中,北方的苍鹰需要继续追逐猎物。由于北方苍鹰的追击速度很高,它们几乎可以在任何情况下追逐猎物,并最终捕获猎物。这种行为的模拟提高了算法对搜索空间的局部搜索能力。假设这种狩猎活动接近于一个半径为R的攻击位置。在第二阶段中,用公式(6)~(8)描述:
x
i
,
j
n
e
w
,
P
2
=
x
i
,
j
+
R
(
2
r
−
1
)
x
i
,
j
(6)
x_{i,j}^{new,P2} = {x_{i,j}} + R(2r - 1){x_{i,j}} \tag{6}
xi,jnew,P2=xi,j+R(2r−1)xi,j(6)
R
=
0.02
(
1
−
t
T
)
(7)
R = 0.02\left( {1 - \frac{t}{T}} \right) \tag{7}
R=0.02(1−Tt)(7)
X
i
=
{
X
i
n
e
w
,
P
2
,
F
i
n
e
w
,
P
2
<
F
i
X
i
,
F
i
n
e
w
,
P
2
≥
F
i
.
(8)
{X_i} = \begin{cases}{} {X_i^{new,P2},}&{F_i^{new,P2} < {F_i}}\\ {{X_i},}&{F_i^{new,P2} \ge {F_i}} \end{cases}. \tag{8}
Xi={Xinew,P2,Xi,Finew,P2<FiFinew,P2≥Fi.(8)
式中:t为当前迭代次数;T为最大迭代次数;
X
i
n
e
w
,
P
2
X_i^{new,P2}
Xinew,P2为第*i*个北方苍鹰的新位置;
x
i
,
j
n
e
w
,
P
2
x_{i,j}^{new,P2}
xi,jnew,P2为第*i*个北方苍鹰的第*j*维的新位置;
x
i
,
j
P
2
x_{i,j}^{P_2}
xi,jP2为基于第2阶段更新后第*i*个鹈鹕的第*j*维的位置;
F
i
n
e
w
,
P
2
F_i^{new,P2}
Finew,P2为基于第2阶段更新后第*i*个北方苍鹰的目标函数值。
算法伪代码如下:

3.实验结果
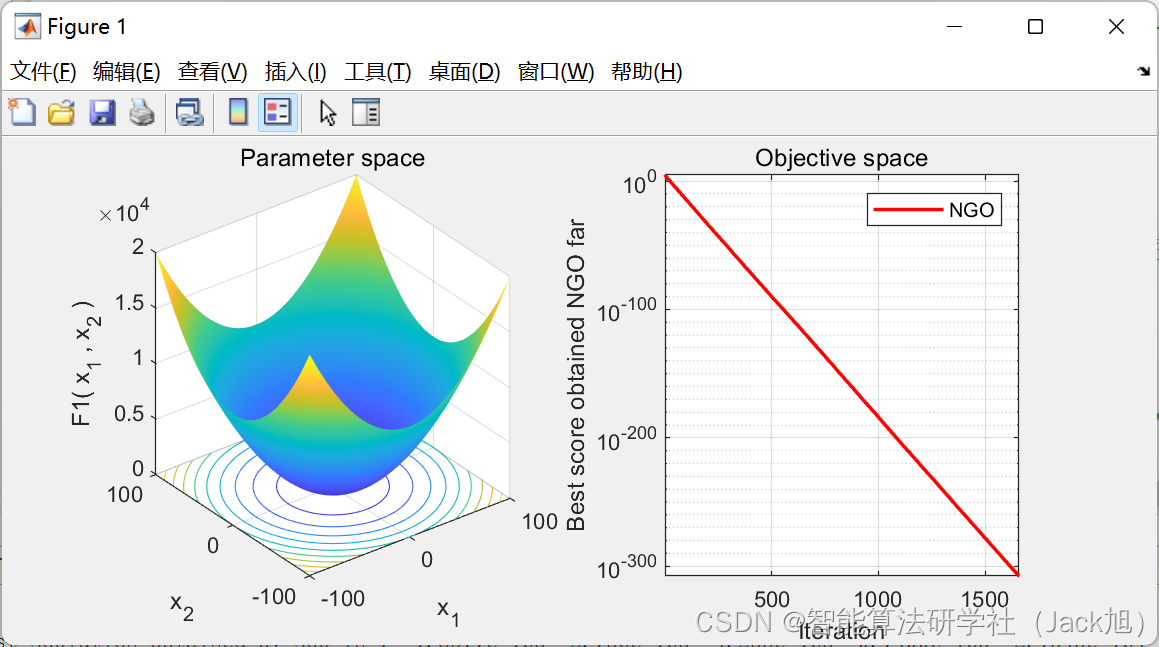
4.参考文献
[1] Hank P , Hamburg. PeliCAN: A New CAN Controller Supporting Diagnosis and System Optimization.
5.Matlab代码
版权归原作者 智能算法研学社(Jack旭) 所有, 如有侵权,请联系我们删除。