
什么是极限学习机?
极限学习机(ELM, Extreme Learning Machines)是一种前馈神经网络,最早由新加坡南洋理工大学黄广斌教授于2006年提出。其发表的文章中对于极限学习机的描述如下:
该算法具有良好的泛化性能以及极快的学习能力
极限学习机和标准神经网络的区别
ELM 不需要基于梯度的反向传播来调整权重,而是通过 Moore-Penrose generalized inverse来设置权值。
标准的单隐藏层神经网络结构如下:
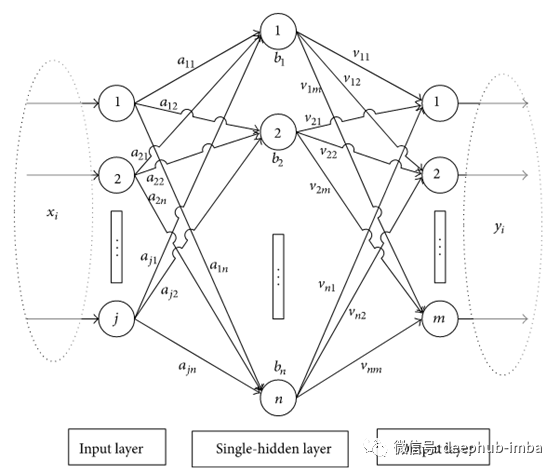
单隐藏层神经网络
其计算过程如下:
- 输入值乘以权重值
- 加上偏置值
- 进行激活函数计算
- 对每一层重复步骤1~3
- 计算输出值
- 误差反向传播
- 重复步骤1~6
而 ELM 则对其进行了如下改进:去除步骤4;用一次矩阵逆运算替代步骤6;去除步骤7。
极限学习机计算过程
具体地,ELM 计算过程如下:

式中:
L 是隐藏单元的数量;
N 是训练样本的数量;
beta 是第 i 个隐藏层和输出之间的权重向量;
w 是输入和输出之间的权重向量;
g 是激活函数;
b 是偏置向量;
x 是输入向量。
极限学习机的计算过程与标准反向传播神经网络十分类似,但是隐藏层与输出之间的权重矩阵是伪逆矩阵。将上式可以简写为:


式中:
m 是输出的数量;
H 是隐藏层输出矩阵;
T 是训练集目标矩阵;
ELM 主要相关理论
定理一:

定理二:

定理三:
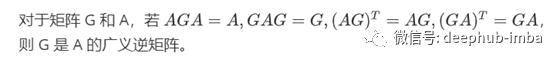
了解了上述定理后,现在我们要做的是定义我们的代价函数。如果输入权重和隐层层偏差可以随机选择,那么SLFN是一个线性系统。
由于我们考虑的 ELM 是一个线性系统,那么可以设计优化函数:
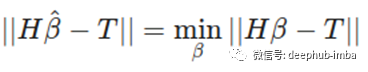
由于 H 是可逆的,所以计算如下:

ELM 算法
ELM 算法主要过程有:
- w_i,b_i,i=1,L 随机初始化
- 计算隐藏层输出 H
- 计算输出权重矩阵

- 利用 beta 在新的数据集上进行预测 T
Python 应用案例见https://github.com/burnpiro/elm-pure
其中,基础的 ELM 算法就能够在 MNIST 数据集达到 91%以上的准确率,并且在 intel i7 7820X CPU 平台上通过 3s 就能够计算完成。
性能对比
首次提出 ELM 的论文中,于2006年通过 Pentium 4 1.9GHz CPU 用 ELM 方法对不同的数据集进行了计算,结果如下:


很明显梯度下降比矩阵反转需要更长的训练时间。此结果表中最重要的信息是准确性和节点数。在前两个数据集中,可以看到作者使用了不同大小的BP来获得与ELM相同的结果。在第一种情况下,BP网络的大小是原来的5倍,在第二种情况下,BP网络的大小是原来的2倍。也说明了 ELM 方法在逼近数据集时有很高的精确性。
本文也对两个具有代表性的数据集(CIFAR-10, MNIST)进行了分析,结果如下:
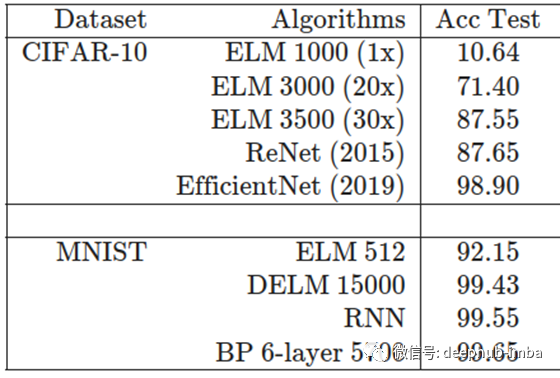
总结
ELM 算法虽然没有传统神经网络的准确度高,但是可以被用于需要即时计算的场景中。
DeepHub
微信号 : deephub-imba
每日大数据和人工智能的重磅干货
大厂职位内推信息
长按识别二维码关注 ->
好看就点在看!********** **********