大家好,我是微学AI,今天给大家介绍一下人工智能(pytorch)搭建模型8-利用pytorch搭建一个BiLSTM+CRF模型,实现简单的命名实体识别,BiLSTM+CRF 模型是一种常用的序列标注算法,可用于词性标注、分词、命名实体识别等任务。本文利用pytorch搭建一个BiLSTM+CRF模型,并给出数据样例,通过一个简单的命名实体识别(NER)任务来演示模型的训练和预测过程。文章将分为以下几个部分:
1. BiLSTM+CRF模型的介绍
2. BiLSTM+CRF模型的数学原理
3. 数据准备
4. 模型搭建
5. 训练与评估
6. 预测
7. 总结
1. BiLSTM+CRF模型的介绍
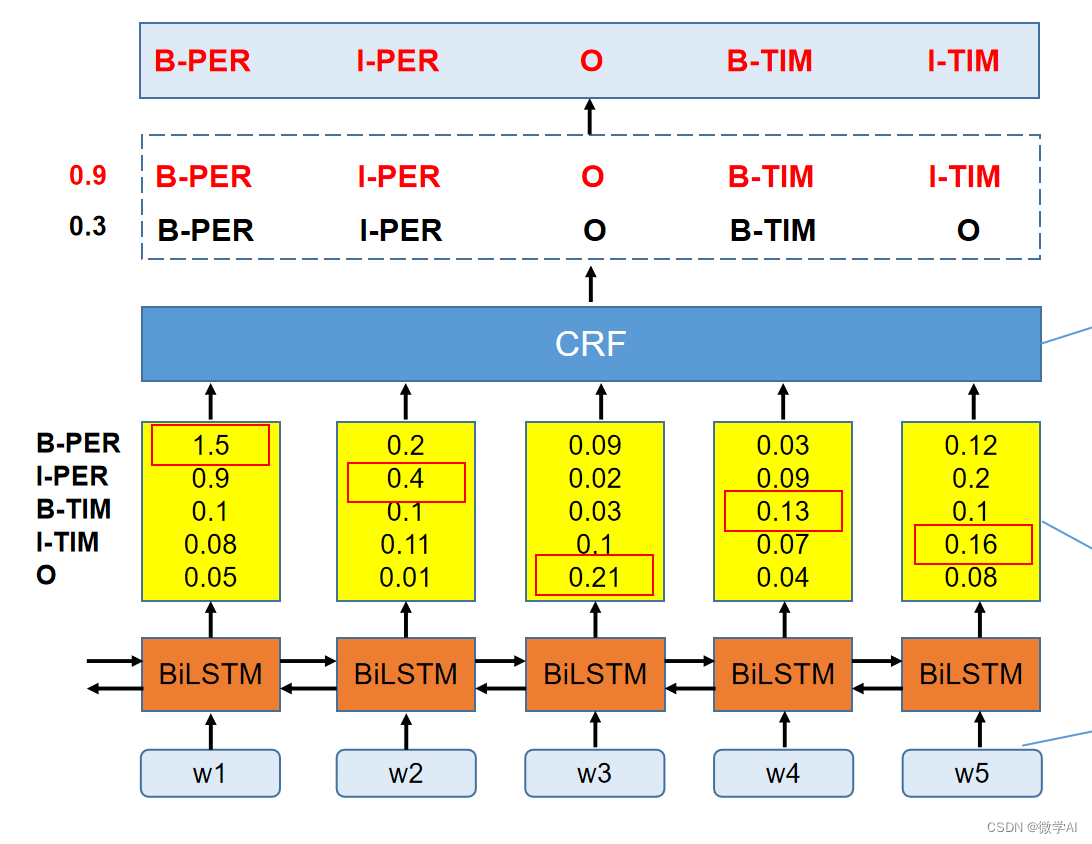
BiLSTM+CRF模型结合了双向长短时记忆网络(BiLSTM)和条件随机场(CRF)两种技术。BiLSTM用于捕捉序列中的上下文信息,而CRF用于解决标签之间的依赖关系。实际上,BiLSTM用于为每个输入序列生成一个特征向量,然后将这些特征向量输入到CRF层,以便为序列中的每个元素分配一个标签。BiLSTM 和 CRF 结合在一起,使模型即可以像 CRF 一样考虑序列前后之间的关联性,又可以拥有 LSTM 的特征抽取及拟合能力。
2.BiLSTM+CRF模型的数学原理
假设我们有一个序列
x
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
\boldsymbol{x} = (x_1, x_2, ..., x_n)
x=(x1,x2,...,xn),其中
x
i
x_i
xi 是第
i
i
i 个位置的输入特征。我们要对每个位置进行标注,即为每个位置
i
i
i 预测一个标签
y
i
y_i
yi。标签集合为
Y
=
y
1
,
y
2
,
.
.
.
,
y
n
\mathcal{Y}={y_1, y_2, ..., y_n}
Y=y1,y2,...,yn,其中
y
i
∈
L
y_i \in \mathcal{L}
yi∈L,
L
\mathcal{L}
L 表示标签的类别集合。
BiLSTM用于从输入序列中提取特征,它由两个方向的LSTM组成,分别从前向后和从后向前处理输入序列。在时间步
t
t
t,BiLSTM的输出为
h
t
∈
R
2
d
h_t \in \mathbb{R}^{2d}
ht∈R2d,其中
d
d
d 是LSTM的隐藏状态维度。具体来说,前向LSTM从左至右处理输入序列
x
\boldsymbol{x}
x,输出隐状态序列
h
→
=
(
h
1
→
,
h
2
→
,
.
.
.
,
h
n
→
)
\overrightarrow{h}=(\overrightarrow{h_1},\overrightarrow{h_2},...,\overrightarrow{h_n})
h=(h1,h2,...,hn),其中
h
t
→
\overrightarrow{h_t}
ht 表示在时间步
t
t
t 时前向LSTM的隐藏状态;后向LSTM从右至左处理输入序列
x
\boldsymbol{x}
x,输出隐状态序列
h
←
=
(
h
1
←
,
h
2
←
,
.
.
.
,
h
n
←
)
\overleftarrow{h}=(\overleftarrow{h_1},\overleftarrow{h_2},...,\overleftarrow{h_n})
h=(h1,h2,...,hn),其中
h
t
←
\overleftarrow{h_t}
ht 表示在时间步
t
t
t 时后向LSTM的隐藏状态。则每个位置
i
i
i 的特征表示为
h
i
=
[
h
i
→
;
h
i
←
]
h_i=[\overrightarrow{h_i};\overleftarrow{h_i}]
hi=[hi;hi],其中
[
⋅
;
⋅
]
[\cdot;\cdot]
[⋅;⋅] 表示向量拼接操作。
CRF用于建模标签之间的关系,并进行全局优化。CRF模型定义了一个由
Y
\mathcal{Y}
Y 构成的联合分布
P
(
y
∣
x
)
P(\boldsymbol{y}|\boldsymbol{x})
P(y∣x),其中
y
=
(
y
1
,
y
2
,
.
.
.
,
y
n
)
\boldsymbol{y} = (y_1, y_2, ..., y_n)
y=(y1,y2,...,yn) 表示标签序列。具体来说,CRF模型将标签序列的概率分解为多个位置的条件概率的乘积,即
P
(
y
∣
x
)
=
∏
i
=
1
n
ψ
i
(
y
i
∣
x
)
∏
i
=
1
n
−
1
ψ
i
,
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
P(\boldsymbol{y}|\boldsymbol{x})=\prod_{i=1}^{n}\psi_i(y_i|\boldsymbol{x}) \prod_{i=1}^{n-1}\psi_{i,i+1}(y_i,y_{i+1}|\boldsymbol{x})
P(y∣x)=i=1∏nψi(yi∣x)i=1∏n−1ψi,i+1(yi,yi+1∣x)
其中
ψ
i
(
y
i
∣
x
)
\psi_i(y_i|\boldsymbol{x})
ψi(yi∣x) 表示在位置
i
i
i 时预测标签为
y
i
y_i
yi 的条件概率,
ψ
i
,
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
\psi_{i,i+1}(y_i,y_{i+1}|\boldsymbol{x})
ψi,i+1(yi,yi+1∣x) 表示预测标签为
y
i
y_i
yi 和
y
i
+
1
y_{i+1}
yi+1 的联合概率。这些条件概率和联合概率可以用神经网络来建模,其中输入为位置
i
i
i 的特征表示
h
i
h_i
hi。
CRF模型的全局优化问题可以通过对数似然函数最大化来实现,即
max
y
log
P
(
y
∣
x
)
=
∑
i
=
1
n
log
ψ
i
(
y
i
∣
x
)
∑
i
=
1
n
−
1
log
ψ
i
,
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
\max_{\boldsymbol{y}}\log P(\boldsymbol{y}|\boldsymbol{x}) = \sum_{i=1}^{n}\log\psi_i(y_i|\boldsymbol{x}) \sum_{i=1}^{n-1}\log\psi_{i,i+1}(y_i,y_{i+1}|\boldsymbol{x})
ymaxlogP(y∣x)=i=1∑nlogψi(yi∣x)i=1∑n−1logψi,i+1(yi,yi+1∣x)
其中
y
\boldsymbol{y}
y 是所有可能的标签序列。可以使用动态规划算法(如维特比算法)来求解全局最优标签序列。
综上所述,BiLSTM+CRF模型的数学原理可以表示为:
P
(
y
∣
x
)
=
∏
i
=
1
n
ψ
i
(
y
i
∣
x
)
∏
i
=
1
n
−
1
ψ
i
,
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
P(\boldsymbol{y}|\boldsymbol{x}) = \prod_{i=1}^{n}\psi_i(y_i|\boldsymbol{x}) \prod_{i=1}^{n-1}\psi_{i,i+1}(y_i,y_{i+1}|\boldsymbol{x})
P(y∣x)=i=1∏nψi(yi∣x)i=1∏n−1ψi,i+1(yi,yi+1∣x)
其中
ψ
i
(
y
i
∣
x
)
=
exp
(
W
o
T
h
i
+
b
o
T
y
i
)
∑
y
i
′
∈
L
exp
(
W
o
T
h
i
+
b
o
T
y
i
′
)
\psi_i(y_i|\boldsymbol{x}) = \frac{\exp(\boldsymbol{W}_o^{T}\boldsymbol{h}_i + \boldsymbol{b}_o^{T}\boldsymbol{y}i)}{\sum{y_i'\in\mathcal{L}}\exp(\boldsymbol{W}_o^{T}\boldsymbol{h}_i + \boldsymbol{b}_o^{T}\boldsymbol{y}_i')}
ψi(yi∣x)=∑yi′∈Lexp(WoThi+boTyi′)exp(WoThi+boTyi)
ψ
i
,
i
+
1
(
y
i
,
y
i
+
1
∣
x
)
=
exp
(
W
t
T
y
i
,
i
+
1
)
∑
y
i
′
∈
L
∑
y
i
+
1
′
∈
L
exp
(
W
t
T
y
i
′
,
i
+
1
′
)
\psi_{i,i+1}(y_i,y_{i+1}|\boldsymbol{x}) = \frac{\exp(\boldsymbol{W}t^{T}\boldsymbol{y}{i,i+1})}{\sum_{y_i'\in\mathcal{L}}\sum_{y_{i+1}'\in\mathcal{L}}\exp(\boldsymbol{W}t^{T}\boldsymbol{y}{i',i+1}')}
ψi,i+1(yi,yi+1∣x)=∑yi′∈L∑yi+1′∈Lexp(WtTyi′,i+1′)exp(WtTyi,i+1)
其中
W
o
\boldsymbol{W}_o
Wo 和
b
o
\boldsymbol{b}_o
bo 是输出层的参数,
W
t
\boldsymbol{W}_t
Wt 是转移矩阵,
h
i
\boldsymbol{h}_i
hi 是位置
i
i
i 的特征表示,
y
i
\boldsymbol{y}i
yi 是位置
i
i
i 的标签表示,
y
i
,
i
+
1
\boldsymbol{y}{i,i+1}
yi,i+1 是位置
i
i
i 和
i
+
1
i+1
i+1 的标签联合表示。
3. 数据准备
下面我将使用一个简单的命名实体识别(NER)任务来演示模型的训练和预测过程。数据集包含了一些句子,每个句子中的单词都被标记为“B-PER”(人名开始)、“I-PER”(人名中间)、“B-LOC”(地名开始)、“I-LOC”(地名中间)或“O”(其他)。
数据样例:
John B-PER
lives O
in O
New B-LOC
York I-LOC
. O
4. 模型搭建
首先,我们需要安装PyTorch库:
pip install torch
接下来,我们将使用PyTorch搭建BiLSTM+CRF模型。完整的模型代码如下:
import torch
import torch.nn as nn
import torch.optim as optim
from TorchCRF import CRF
classBiLSTM_CRF(nn.Module):def__init__(self, vocab_size, tag_to_ix, embedding_dim, hidden_dim):super(BiLSTM_CRF, self).__init__()
self.embedding_dim = embedding_dim
self.hidden_dim = hidden_dim
self.vocab_size = vocab_size
self.tag_to_ix = tag_to_ix
self.tagset_size =len(tag_to_ix)
self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim //2,
num_layers=1, bidirectional=True)
self.hidden2tag = nn.Linear(hidden_dim, self.tagset_size)
self.crf = CRF(self.tagset_size)defforward(self, sentence):
embeds = self.word_embeds(sentence).view(len(sentence),1,-1)
lstm_out, _ = self.lstm(embeds)
lstm_out = lstm_out.view(len(sentence), self.hidden_dim)
lstm_feats = self.hidden2tag(lstm_out)return lstm_feats
defloss(self, sentence, tags):
feats = self.forward(sentence)return-self.crf(torch.unsqueeze(feats,0), tags)defpredict(self, sentence):
feats = self.forward(sentence)return self.crf.decode(torch.unsqueeze(feats,0))
5. 训练与评估
接下来,我们将使用训练数据对模型进行训练,并在每个epoch后打印损失值和准确率。
deftrain(model, optimizer, data):for epoch inrange(10):
total_loss =0
total_correct =0
total_count =0for sentence, tags in data:
model.zero_grad()
loss = model.loss(sentence, tags)
loss.backward()
optimizer.step()
total_loss += loss.item()
prediction = model.predict(sentence)
total_correct +=sum([1for p, t inzip(prediction, tags)if p == t])
total_count +=len(tags)print(f"Epoch {epoch +1}: Loss = {total_loss /len(data)}, Accuracy = {total_correct / total_count}")
6. 预测
最后,我们将使用训练好的模型对新的句子进行预测。
defpredict(model, sentence):
prediction = model.predict(sentence)return[p for p in prediction]
7. 总结
用训练好的模型对新的句子进行预测。
defpredict(model, sentence):
prediction = model.predict(sentence)return[p for p in prediction]
7. 总结
本文介绍了如何使用PyTorch搭建一个BiLSTM+CRF模型,并通过一个简单的命名实体识别(NER)任务来演示模型的训练和预测过程。希望这篇文章能帮助你理解BiLSTM+CRF模型的原理,并为你的实际项目提供参考作用哦。
更新精彩的模型搭建与应用请持续关注哦!
版权归原作者 微学AI 所有, 如有侵权,请联系我们删除。