分割常用损失函数

1.交叉熵

交叉熵损失公式：

其中表示真实标签，表表示预测结果。

优点：交叉熵Loss可以用在大多数语义分割场景中。

缺点：对于只分割前景和背景的时候，当前景像素的数量远远小于背景像素的数量时，即y=0的数量远远大于y=1的数量，损失函数中y=0的成分就会占据主导，使得模型严重偏向背景，导致效果不好。（该缺点对二分类不友好。eg：医学图像分割）

2.加权交叉熵

加权交叉熵损失公式：

3.BCELoss（Binary Cross Entropy）

公式：

特点：基本等价于二分类情况下的交叉熵，通产接sigmoid激活函数的输出。

4.Focal Loss

源自目标检测方向，是对标准交叉熵的一种改进，主要解决难易样本数量不平衡的问题。当正负样本数量不平衡时，可以通过在交叉熵中引入参数进行调节。

应用场景：易分样本多，难分样本少

CE公式：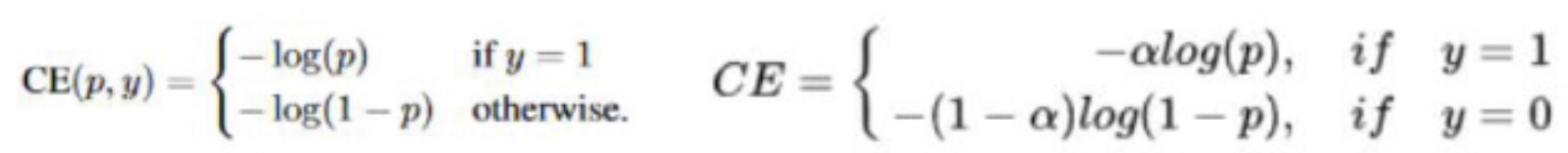

虽然上述公式平衡了正负样本的数量，但实际上，目标检测中的大量的候选目标都是易分样本。这些样本的损失很低，但是由于数量极不平衡，易分样本的数量相对来讲太多，最终主导了总的损失。目前Focal Loss在分割方向主要适用于二分类问题。

因此，Focal Loss认为易分样本对模型的提升效果非常小，模型应该主要关注那些难分样本。

FL公式：

参数P：当P→0时，调制因子（1-P）接近1，损失不被影响；当P→1时，（1-P）接近0，从而减少易分样本对总loss的贡献。

参数γ：当γ=0时，Focal Loss就是传统的交叉熵。当γ增加时，调制系数也会增加。当γ为定值时，比如等于2，easy example（P=0.9）的loss要比标准的交叉熵小100+倍，当P=0.968时，要小1000+倍。但是对于hard example（P＜0.5），loss最多小了4倍。这样的话hard example的权重相对提升了很多，从而增加了那些误分的重要性。实验表明，γ=2，α=0.75时效果最好。

α：控制正负样本不平衡

γ：控制难易样本不平衡

5.Dice Loss

Dice系数：是用来度量集合相似度的函数，通常用于计算两个样本之间的像素相似度

公式：

(分母上的2为了平衡分子的2)

TP：真实为1，预测为1；FP：真实为0，预测为1

FN：真实为1，预测为0；TN：真实为0，预测为0

如下图所示

Dice Loss适用于样本极度不均衡的情况，一般情况下使用Dice Loss会对反向传播有不利的影响，是的训练不稳定。

Dice Loss公式：

6.IoU Loss

IoU Loss公式：

7.Jaccard 系数

Jaccard系数：定义为A与B交集的大小与A与B并集的大小的比值。

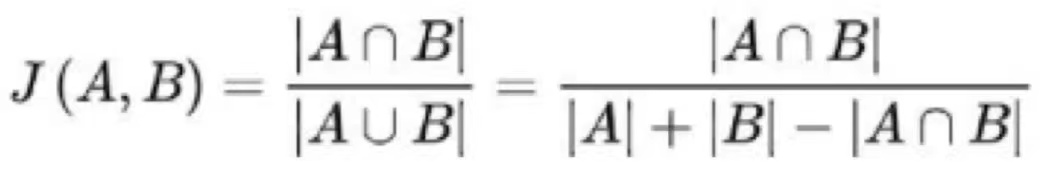
8.Tversky系数

Tversky系数：是Dice系数和Jaccard系数的广义系数

当α和β均为0.5时，这个公式就是Dice系数，当α和β均为1时，这个公式就是Jaccard系数。通过调整α和β这两个超参数可以控制这两者之间的权衡，进而影响召回率等指标。

9.Lovasz-Softmax Loss

Lovasz-Softmax Loss：对Jaccard进行扩展，表现更好

10.BCE Loss + Dice Loss

BCE Loss + Dice Loss：将BCE Loss和Dice Loss进行组合，在数据较为均衡的情况下有所改善，但是再数据极度不均衡的情况下交叉熵会在迭代几个Epoch之后远远小于Dice Loss，这个组合Loss会退化为Dice Loss

11.Focal Loss + Dice Loss

Focal Loss + Dice Loss：论文提出了使用Focal Loss和Dice Loss来处理小器官的分割问题。关注难分样本。