在时间序列预测中,脏乱数据的存在会影响最终的预测结果。这是肯定的,尤其是在这个领域,因为时间依赖性在处理时间序列时起着至关重要的作用。

噪音或异常值必须按照特别的解决方案小心处理。在这种情况下,tsmoothie包可以帮助我们节省大量时间来准备用于分析的时间序列。Tsmoothie是一个用于时间序列平滑和离群值检测的python库,它可以以向量化的方式处理多个序列。它很有用,因为它可以提供我们需要的预处理步骤,如去噪或离群值去除,保留原始数据中的时间模式。
在这篇文章中,我们使用这些小工具来改进预测任务。更准确地说,我们试图预测太阳能电池板的日发电量。最后,我们期望能从去噪过程中获益,并产生比未进行预处理的情况更好的预测。
数据
Kaggle上有一个真实的数据集。这些数据存储了安装在私人住宅屋顶上的太阳能电池板每天的发电量。数据记录自2011年,以时间序列的形式呈现3个不同的来源:
- 房子每天的煤气消耗量。
- 房屋的日常耗电量。当值为负值时,表示太阳能超过当地的电力消耗。
- 功率表在直流到交流转换器上的日值。这是当前累积的太阳能。我们不需要累积值,相反,我们需要绝对的日值,因此,我们做了一个简单的区分。这是我们要预测的目标。
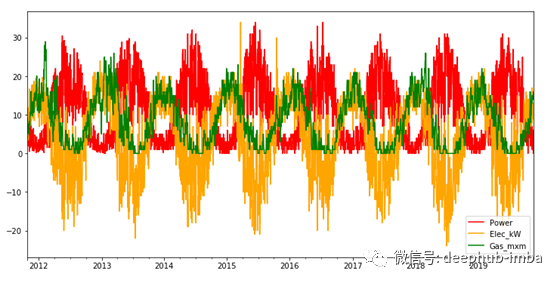
正如我们可以从原始系列的情节中注意到的,有很多噪音存在。这是正常的数据登记的传感器。如果我们的数据源受到外部气象条件的影响,或者传感器质量不佳,位置不理想,情况会更糟。
幸运的是,我们有知识和工具来实现我们的预测任务的良好结果。
时间序列平滑
我们工作流程中的第一步是时间序列预处理。我们的战略非常直观和有效。我们取目标时间序列(发电量),并用一种奇妙的工具使其平滑:卡尔曼滤波器,这是每个数据科学家都必须知道的。
一般来说,在时间序列任务中,使用卡尔曼滤波的最大优点是可以使用状态空间形式来表示未观察到的组件模型。以状态空间形式表示时间序列模型的范围是可用性的一套通用算法(包括卡尔曼滤波),用于计算高斯似然,可以在数值上最大化,得到模型参数的最大似然估计。著名的软件使用这种表示来匹配像ARIMA这样的模型并非偶然。在我们的特殊情况下,我们使用卡尔曼滤波器和状态空间表示来构建一个未观察组件模型。
到目前为止所解释的一切听起来可能很棘手,但我想向您保证……Tsmoothie可以轻松地构建未观察到的组件模型,以非常简单和有效的方式操作定制的Kalman平滑。在这个阶段,我们可以释放我们的想象力,从水平、趋势、季节性、长季节性中发现哪些成分有助于创建我们正在观察的时间序列。365天的水平和漫长的季节对我们来说很好。我们只需为每个组件假设添加一个“置信度”,就完成了。

卡尔曼平滑的可视化展示
结果平滑的时间序列保持相同的时间模式存在于原始数据,但具有一致和合理的降噪。
专业提示:如果我们的系列中包含nan,这不是一个问题,卡尔曼平滑会工作得非常好,它是一个非常强大的工具,以填补我们的数据空白……这是卡尔曼平滑的美丽。
时间序列预测
第二步是建立一个神经网络结构来预测未来几天的发电量。首先对原始数据拟合模型,然后对平滑后的序列进行拟合。平滑数据仅作为目标变量使用,所有输入序列保持原始格式。使用平滑标签的目的是为了帮助模型更好地捕捉真实模式和去除噪声。
我们选择一个LSTM自动编码器来预测接下来的5个日发电量值。训练程序使用keras-hypetune进行。该框架以非常直观的方式提供了神经网络结构的超参数优化。我们对一些参数组合进行网格搜索。
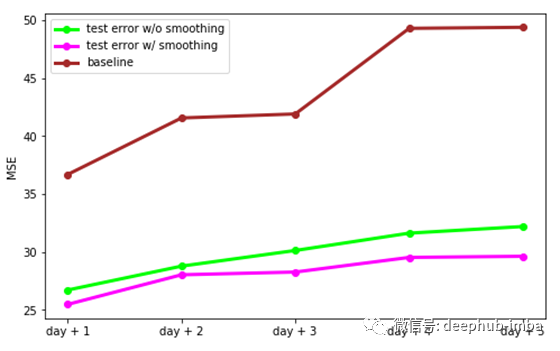
我们可以想象,预测误差与时间范围有关。对第二天的预测比对未来五天的预测更准确。重要的一点是,平滑过程提供了很大的好处,在预测精度的所有时间跨度。
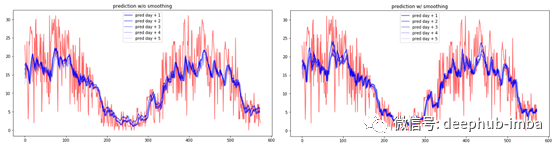
总结
在这篇文章中,我们利用了预测场景中的时间序列平滑。应用卡尔曼滤波平滑使得原始数据和减少噪声的存在。这种选择在预测精度方面被证明是有利的。我还想指出卡尔曼滤波在这个应用程序中的威力,以及它在构建未观察组件模型时是一个很好的工具的能力。
本文代码:https://github.com/cerlymarco/MEDIUM_NoteBook
作者:Marco Cerliani
deephub翻译组