**🐦🐦🐦 **
每一个统计学问题,我们都需要对其先做一些基本假设。在时间序列分析中,我们考虑了很多合理且可以简化问题的假设,而其中最重要的假设就是平稳。本文结合两个数据集的例子来浅谈什么是时间序列的平稳性,为什么要检验时间序列的平稳性,并介绍了三种由浅入深的检验方法。
什么是时间序列平稳性
通常我们所说的预测(forecast)是利用事物特征变量的历史和现状来推测未来可能出现的状况。我们假设时间序列的基本特性必须能从过去维持到我们推测的时期,否则,基于历史和现状来预测未来将变得不可靠。时间序列的平稳性,简单理解就是时间序列的基本特性维持不变,换句话说,所谓平稳性就是要求由样本时间序列所得到的曲线在未来的一段时期内仍能沿着现有的形态持续下去。
为什么要检验时间序列平稳性
很多变量之所以难以估计,是因为这些变量经常发生突变,不是平稳的时间序列。时间序列的平稳性是经典时间序列分析的基本假设前提,只有基于平稳的时间序列进行的预测才是有效的。
经典的时间序列分析预测,和经典的分类回归统计预测模型,要求我们的观测点(observations)的基本统计值是有一致性的,也就是要求输入的时间序列是平稳的;对于非平稳时间序列(比如有季节性),一种方法是采用季节期间和非季节期间分开训练预测,然而通常效果并不好,所以对于非平稳时间序列的预测问题,最好使用机器学习模型来解决。
总之,对于经典的时间序列分析,和经典的分类回归统计预测模型来说,检验时间序列的平稳性是非常必要的。
检验时间序列平稳性的三种方法
方法1. 通过绘图直观判断
我们用两个数据集来做演示,分别是某家医院每天出生的女婴数量,和某航空公司1949-1961年的国际航班旅客数量。
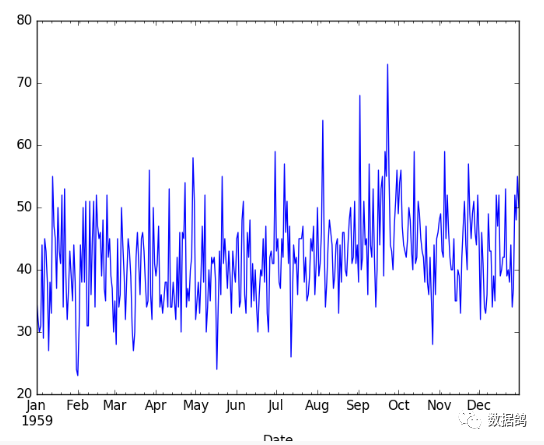
读入女婴出生数量数据集,绘制折线图和直方图:
import pandas as pdfrom matplotlib import pyplotbirth_series = pd.read_csv('../data/daily-total-female-births.csv', header=0, index_col=0)birth_series.plot()pyplot.show()
birth_series.hist()pyplot.show()
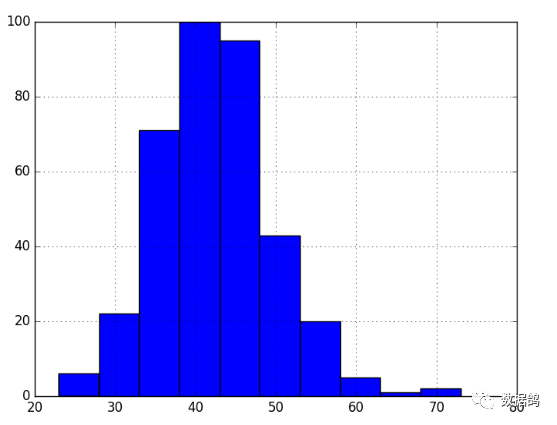
可以看出,女婴出生数量数据集的观测点不存在随时间变化的趋势性或者季节性,从直方图可以看出其分布是类似于正态分布,因此可以判断为是平稳时间序列。
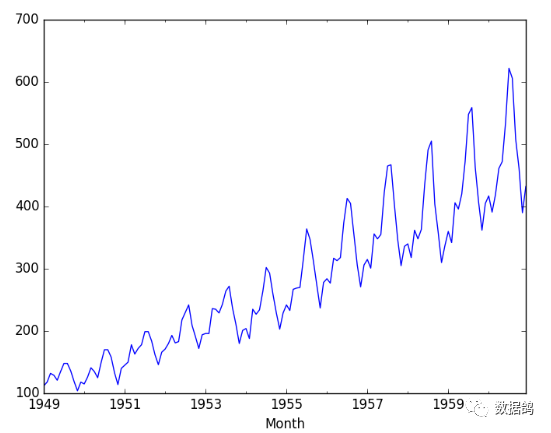
再看另外一个例子,读入国际航班旅客数据集,绘制折线图和直方图:
airline_series = pd.read_csv('../data/airline-passengers.csv', header=0, index_col=0)airline_series.plot()pyplot.show()
airline_series.hist()pyplot.show()
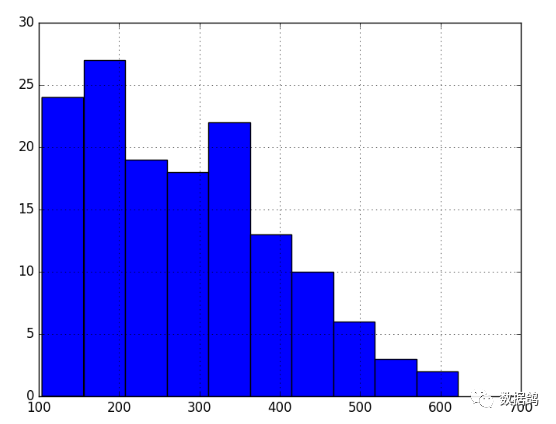
可以看出,国际旅客数量是有季节性的,而且总体来说是呈现逐年上升趋势,从直方图上看分布明显不是正态分布,因此可以判断为非平稳时间序列。
方法2. 通过基本统计值判断
平稳时间序列的基本统计值,或称摘要统计值(summary statistics)在不同时期是一致的,比如均值(mean)和方差(variance)。
下面我们把时间序列一切为二,看下前后两期的摘要统计值的对比,先来看女婴出生数序列:
X = birth_series.valuessplit = round(len(X) / 2)X1, X2 = X[0:split], X[split:]mean1, mean2 = X1.mean(), X2.mean()var1, var2 = X1.var(), X2.var()print('mean1=%f, mean2=%f' % (mean1, mean2))print('variance1=%f, variance2=%f' % (var1, var2))
输出:
mean1=39.763736, mean2=44.185792
variance1=49.213410, variance2=48.708651
OK,可以看到前后两期的均值和方差基本是一致的,女婴出生数时间序列可以判断为平稳时间序列。
再来看下国际航空旅客序列:
X = airline_series.valuessplit = round(len(X) / 2)X1, X2 = X[0:split], X[split:]mean1, mean2 = X1.mean(), X2.mean()var1, var2 = X1.var(), X2.var()print('mean1=%f, mean2=%f' % (mean1, mean2))print('variance1=%f, variance2=%f' % (var1, var2))
输出:
mean1=182.902778, mean2=377.694444
variance1=2244.087770, variance2=7367.962191
前期和后期统计值差了很多,后期的均值和方差是前期的几倍,因此国际航班旅客数时间序列可以判断为是非平稳时间序列。
**方法3. 通过假设检验判断 **
图形观察方式很直观,但也很主观,不同的人对相同的图形,可能得出不同的结论。基本统计值比图形判断严谨一些,但是同样,不同时期的摘要统计值的对比还是人为判断,而且像例子里面只是从中间时间点一刀切来对比了统计值,略显粗略。因此需要一个更加客观的统计方法来检验时间序列的平稳性,即单位根检验,常见的单位根检验方法有DF检验、ADF检验和PP检验,下面主要介绍如何使用Python进行ADF单位根检验。
单位根检验背后的动机就是看一个时间序列的趋势性有多强:
- 原(H0) 假设:存在单位根,时间序列是非平稳的,存在和时间相关的趋势性,p值 > 0.05;
- 备择(H1) 假设:原假设被推翻,时间序列是平稳的,不存在时间相关趋势性或者季节性, p值 <= 0.05。
下面我们来检验女婴出生数时间序列:
from statsmodels.tsa.stattools import adfullerX = birth_series.valuesX.shape = (len(X),)result = adfuller(X)print('ADF Statistic: %f' % result[0])print('p-value: %f' % result[1])print('Critical Values:')for key, value in result[4].items(): print('\t%s: %.3f' % (key, value))
输出为:
ADF Statistic: -4.808291
p-value: 0.000052
Critical Values:
1%: -3.449
5%: -2.870
10%: -2.571
可以看到结果是-4,负数的绝对值越大,我们越倾向推翻原假设,也就是我们的时间序列是平稳的。从统计上看,我们的-4有1%的可能性是小于- 3.449。
再来检验国际航班旅客数时间序列:
from statsmodels.tsa.stattools import adfullerX = airline_series.valuesX.shape = (len(X),)result = adfuller(X)print('ADF Statistic: %f' % result[0])print('p-value: %f' % result[1])print('Critical Values:')for key, value in result[4].items(): print('\t%s: %.3f' % (key, value))
输出:
ADF Statistic: 0.815369
p-value: 0.991880
Critical Values:
1%: -3.482
5%: -2.884
10%: -2.579
检验值是正的,倾向接受原假设,时间序列是非平稳的。
总结
- 平稳性检验对于时间序列分析来说是非常必要的。
- 可以通过绘图直观判断平稳性,也可以通过摘要统计值来判断。
- 更严谨的判断方法是假设检验,本文介绍了如何使用Python进行ADF单位根检验。
DeepHub
微信号 : deephub-imba
每日大数据和人工智能的重磅干货
大厂职位内推信息
长按识别二维码关注 ->
好看就点在看!********** **********