前言
在主成分和因子分析中,我们对降维算法做了总结。这里我们就对另外一种经典的降维方法线性判别分析(Linear Discriminant Analysis, 以下简称LDA)做一个总结。LDA在模式识别领域(比如人脸识别,舰艇识别等图形图像识别领域)中有非常广泛的应用,因此我们有必要了解下它的算法原理。
在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),他是一种处理文档的主题模型。我们本文只讨论线性判别分析,因此后面所有的LDA均指线性判别分析。
在做具体解释之前,请允许我放上我之前的一些链接:
主成分分析 —— matlab :传送门
主成分分析 —— python :传送门
因子分析 —— matlab :传送门
因子分析 —— python :传送门
正题
1.LDA的思想
线性判别分析((Linear Discriminant Analysis ,简称 LDA)是一种经典的线性学习方法,在二分类问题上因为最早由 [Fisher,1936] 提出,亦称 ”Fisher 判别分析“。并且LDA也是一种监督学习的降维技术,也就是说它的数据集的每个样本都有类别输出。这点与主成分和因子分析不同,因为它们是不考虑样本类别的无监督降维技术。
LDA 的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同样样例的投影尽可能接近、异样样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。其实可以用一句话概括:就是“投影后类内方差最小,类间方差最大”。
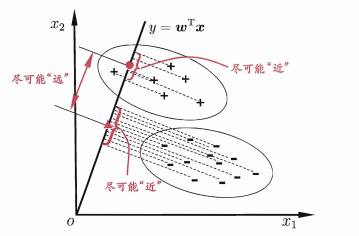
图为 LDA的二维示意图。”+“,”-“分别代表正侧和反侧,椭圆表示数据簇的外轮廓,虚线表示投影,红色实心圆和实心三角形分别表示两类样本投影后的中心点。
2. 瑞利商(Rayleigh quotient)与广义瑞利商(genralized Rayleigh quotient)
我们先来看一下瑞丽商的定义。
瑞丽商是指这样的函数R(A,x):
其中x为非零向量,而A为 n*n 的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵,即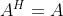 . 如果我们的矩阵A是实矩阵,则满足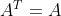的矩阵即为Hermitan矩阵。
瑞利商R(A,x)有一个非常重要的性质,即它的最大值等于矩阵A最大的特征值,而最小值等于矩阵A的最小的特征值,也就是满足
至于证明过程就不在这里介绍了。当向量x是标准正交基时,即满足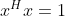时,瑞利商退化为: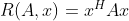,这个形式在谱聚类和PCA中都有出现。
以上就是瑞丽商的内容。
下面我们再来介绍一下广义的瑞丽商,
广义的瑞丽商是指这样的函数 R(A,B,x) :
其中x为非零向量,而A,B为n×n的Hermitan矩阵。B为正定矩阵。它的最大值和最小值是什么呢?其实我们只要通过将其通过标准化就可以转化为瑞利商的格式。我们令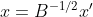,则分母转化为:
而分子转化为:
此时我们的R(A,B,x)转化为R(A,B,x′):
利用前面的瑞利商的性质,我们可以很快的知道,R(A,B,x′)的最大值为矩阵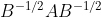的最大特征值,或者说矩阵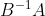的最大特征值,而最小值为矩阵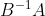的最小特征值。
3. 二类LDA原理
我们先介绍一下稍微简单,容易理解的二分类LDA入手,详细了解一下LDA的原理
首先给定数据集 D={(x1,y1),(x2,y2),...,((xm,ym))} ,其中任意样本xi为n维向量,yi∈{0,1}。另外我们定义Nj(j=0,1)为第j类样本的个数,Xj(j=0,1)为第j类样本的集合,而μj(j=0,1)为第j类样本的均值向量,定义Σj(j=0,1)为第j类样本的协方差矩阵(严格说是缺少分母部分的协方差矩阵)。
其中:
μj的表达式为:
Σj的表达式为:
我们将数据投影到一条直线上即可。我们假设我们的投影直线是向量w,则对任意一个样本本xi,它在直线w的投影为,对于我们的两个类别的中心点μ0,μ1在在直线ww的投影为
和
。
由于LDA需要让不同类别的数据的类别中心之间的距离尽可能的大,也就是我们要最大化 ,同时我们希望同一种类别数据的投影点尽可能的接近,也就是要同类样本投影点的协方差
和
尽可能的小,即最小化
。综上所述,我们的优化目标为:
在这里,大家是否有很多问好???
就是 w , 在哪,怎么算,下面就是我们求解的过程,在本小节最后就是哦!!!
我们一般定义类内散度矩阵Sw为:
同时定义类间散度矩阵Sb为:
全局散度矩阵:
这样我们的优化目标重写为:
仔细一看上式,这不就是我们的广义瑞利商嘛!这就简单了,利用我们第二节讲到的广义瑞利商的性质,我们知道我们的J(w')最大值为矩阵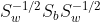的最大特征值,而对应w'为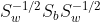 的最大特征值对应的特征向量! 而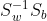的特征值和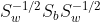的特征值相同,的特征向量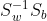的特征向量w和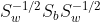的特征向量w′满足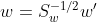的关系!
在这里我们就求到了 w 了哦 !!!
注意到对于二类的时候,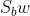的方向恒平行于μ0−μ1,不妨令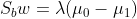,将其带入: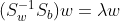,可以得到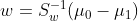, 也就是说我们只要求出原始二类样本的均值和方差就可以确定最佳的投影方向w了。
4.多类LDA原理
前面我们介绍了二分类的LDA,接下来我们再来看看多类别的LDA。
假设我们的数据集,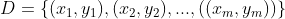,其中任意样本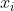 为n维向量,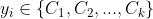 。我们定义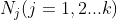为j类样本的个数,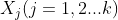为j类样本的集合,而 为第j类样本的均值向量,定义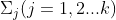 为第j类样本的协方差矩阵。从在二类LDA里面定义的公式可以很容易的类推到多类LDA。
由于我们是多类向低维投影,则此时投影到的低维空间就不是一条直线,而是一个超平面了。假设我们投影到的低维空间的维度为d,对应的基向量为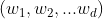,基向量组成的矩阵为W,它是一个n*d的矩阵。
此时我们的优化目标应该可以变成为:
其中,,
为所有样本的均值向量。
但是在这里会有一个问题?
就是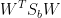 和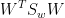都是矩阵,不是标量,无法作为一个标量函数来优化!也就是说,我们无法直接用二类LDA的优化方法,怎么办呢?
一般来说,我们可以用其他的一些替代优化目标来实现。
比如,常见的一个LDA多类优化目标函数定义为:
其中,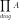 为 A的主对角线元素的乘积,W为n×d的矩阵。
J(W)的优化过程可以转化为:
此时,我再来观察一下上式,会发现最右边的式子,就是我们上面所讲的广义瑞丽商!!!最大值是矩阵的最大特征值,最大的d个值的乘积就是矩阵
的最大的d个特征值的乘积,此时对应的矩阵W为这最大的d个特征值对应的特征向量张成的矩阵。
由于W是一个利用了样本的类别得到的投影矩阵,因此它的降维到的维度d最大值为k-1。为什么最大维度不是类别数k呢?
因为Sb中每个μj−μ的秩为1,因此协方差矩阵相加后最大的秩为k(矩阵的秩小于等于各个相加矩阵的秩的和),但是由于如果我们知道前k-1个μj后,最后一个μk可以由前k-1个μj线性表示,因此Sb的秩最大为k-1,即特征向量最多有k-1个。
5.LDA分类
那么在最佳的分类空间如何对样本进行分类?
1)对二分类问题。由于只有两个类别,在经过上面的求解后,最后所有样本将会映射到一维空间中,设两个不同样本映射后的中心点分别为 ,
;我们将两个类别的中心点之间中心点作为分类点。
最后,我们将
的x分为一类,其他的分为另一类。
2)对多分类问题。通过LDA方法最终将原始数据映射到c-1个维度上,现在我们需要在这c-1个维度上将样本集分成c类。这个怎么分呢?本人暂时也不知道,能想到的只是将问题转化为二分类问题。实际上,对于多类的情况主要考虑用来降维。
对于此类问题,我们主要将它转化为二分类来处理,我们使用一对其余的方法。简单来说就是先将所有c类样本分成1和2c,然后再将2c分为2和3~c,以此类推,直到完全分开。
6.LDA算法流程
输入:数据集 ,其中任意样本xixi为n维向量,
,降维到的维度d。
输出:降维后的样本集D′
计算类内散度矩阵Sw
计算类间散度矩阵Sb
计算矩阵
4)计算的最大的d个特征值和对应的d个特征向量(w1,w2,...wd)得到投影矩阵w
对样本集中的每一个样本特征xi,转化为新的样本
得到输出样本集
二类LDA matlab举例:
1.读取数据集
data = xlsread('文件路径')
2.分离数据集
比如取数据集的前20行,2和3列
data1=data(1:20,2:3)
比如把上面数据集的第一列定义为x,第二列定义为y;然后分类x0,x1
x = data1(:,1)
y = data1(:,2)
x0 = x(find(y==0))
x1 = x(find(y==1))
诸如此类等等,请视情况自行决定,因我手头没有相关例题,只能介绍到这里了
3.求解w
%求均值
u0 = mean(x0);
u1 = mean(x1);
%求协方差
E0 = (x0-u0)'*(x0-u0);
E1 = (x1-u1)'*(x1-u1);
Sw = E0+E1;
Sb = (u0-u1)*(u0-u1)';
w = (Sw)^(-1)*(u0-u1)
4.输出降维后的数据集
predict_y = w'* x
5.分类
u = mean(w'* x)
for i = x
h = w' * i ;
lei = 1*(h<u)
end
好了,这次更改就到这里结束了,后续会增加实例的!
版权归原作者 洋洋菜鸟 所有, 如有侵权,请联系我们删除。