1. 作业内容描述
1.1 背景
- 数据集大小150
- 该数据有4个属性,分别如下 - Sepal.Length:花萼长度(cm)- Sepal.Width:花萼宽度单位(cm)- Petal.Length:花瓣长度(cm)- Petal.Width:花瓣宽度(cm)- category:类别(Iris Setosa\Iris Versicolour\Iris Virginica)
1.2 要求
在不调用机器学习库的情况下,使用贝叶斯分类来预测一个花所属的种类。
2. 作业已完成部分和未完成部分
该作业已经全部完成,没有未完成的部分。全部代码我已经放在GitHub上和colab上了,可以点击下面的链接进行跳转。
 GitHub For BayesianColab For Bayesian
GitHub For BayesianColab For Bayesian
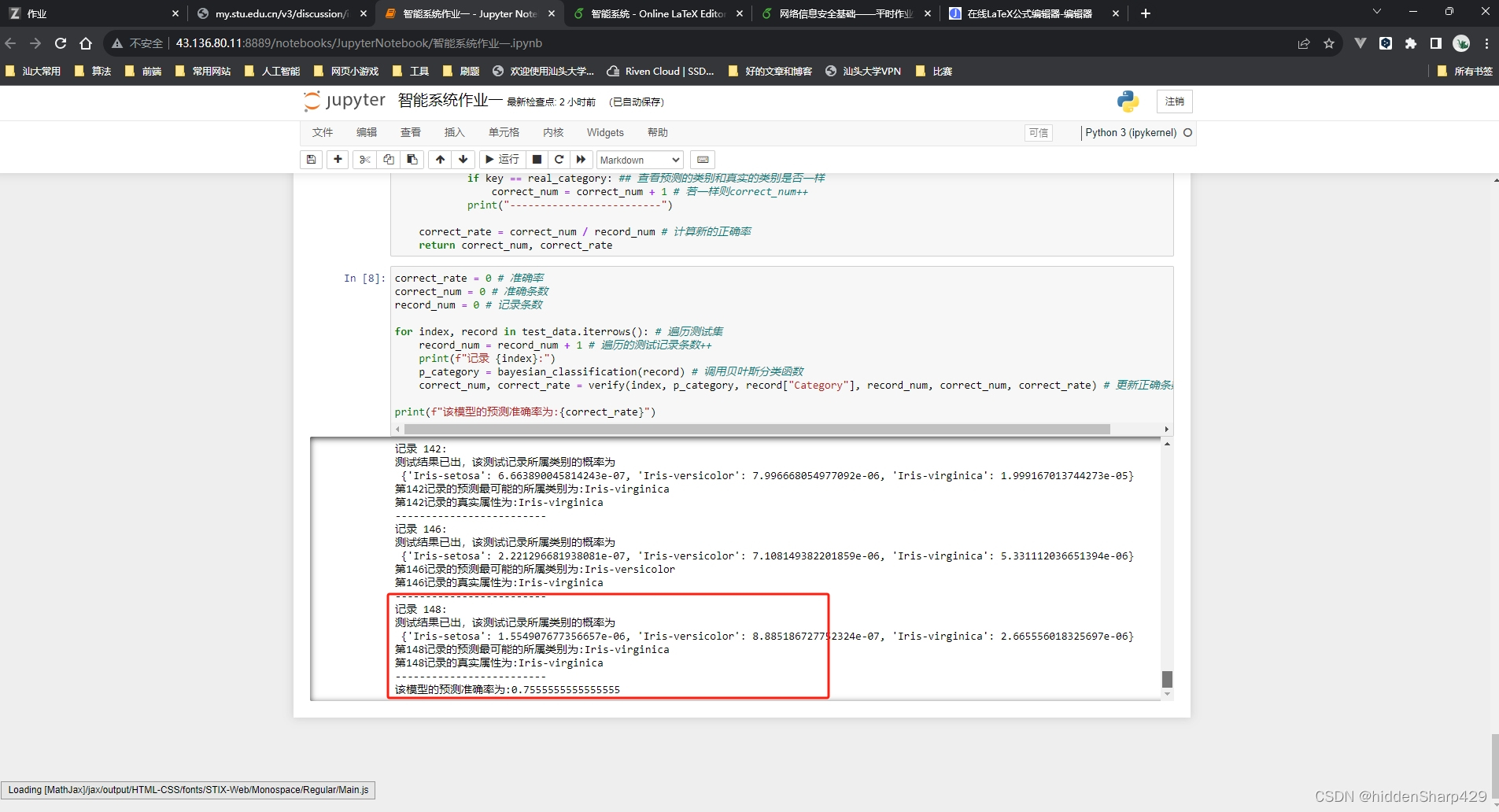
3. 作业运行结果截图
最后得出使用贝叶斯分类的模型预测的准确率为
75
%
→
90
%
75\% \to 90\%
75%→90%
4. 核心代码和步骤
4.1 第一步将数据集读入
4.1.1 原始的数据集 data.txt 部分截图:

稍微进行改动一下(添加了属性列并将格式转换为.csv)
4.1.2 修改后的数据集 data.csv 部分截图
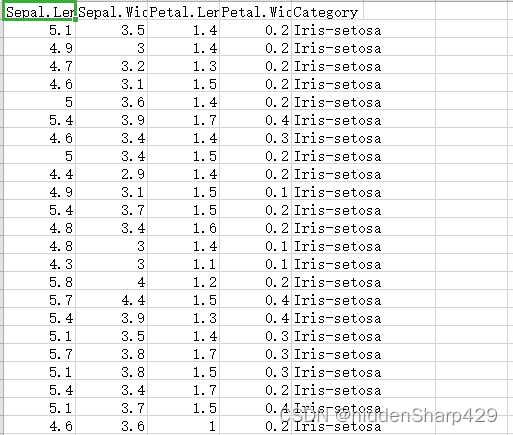
4.1.3 将 data.csv 读入并且将其存入标识符 df 中,定义数据集的筛选条件 expr_1;expr_2;expr_3
- expr_1: 用于赛选 Category 属性列为 iris-setosa 的类 sql 语句
- expr_2: 用于赛选 Category 属性列为 Iris-versicolor 的类 sql 语句
- expr_3: 用于赛选 Category 属性列为 Iris-virginica 的类 sql 语句 用上面定义的筛选条件筛选出数据集中三个类别的数据,并分别存入对应的标识符中。
- Iris_setosa_dataframe:所属类别为 Iris-setosa 的全部数据
- Iris_versicolor_dataframe:所属类别为 Iris-versicolor 的全部数据
- Iris_virginica_dataframe:所属类别为 Iris-virginica 的全部数据
4.1.4 代码部分
In[1]:
import pandas as pd
df = pd.read_csv("data.csv")# 读取全部列表数据
expr_1 ="Category == 'Iris-setosa'"# 用于赛选Category属性列为iris-setosa的类sql语句
expr_2 ="Category == 'Iris-versicolor'"# 用于赛选Category属性列为Iris-versicolor的类sql语句
expr_3 ="Category == 'Iris-virginica'"# 用于赛选Category属性列为Iris-virginica的类sql语句
Iris_setosa_dataframe = df.query(expr_1)
Iris_versicolor_dataframe = df.query(expr_2)
Iris_virginica_dataframe = df.query(expr_3)print("Iris_setosa_dataframe is:\n",Iris_setosa_dataframe)print("Iris_versicolor_dataframe is\n",Iris_versicolor_dataframe)print("Iris_virginica_dataframe is\n",Iris_virginica_dataframe)
out[1]:
Iris_setosa_dataframe is:
Sepal.Length Sepal.Width Petal.Length Petal.Width Category
0 5.1 3.5 1.4 0.2 Iris-setosa
1 4.9 3.0 1.4 0.2 Iris-setosa
2 4.7 3.2 1.3 0.2 Iris-setosa
3 4.6 3.1 1.5 0.2 Iris-setosa
4 5.0 3.6 1.4 0.2 Iris-setosa
5 5.4 3.9 1.7 0.4 Iris-setosa
6 4.6 3.4 1.4 0.3 Iris-setosa
7 5.0 3.4 1.5 0.2 Iris-setosa
8 4.4 2.9 1.4 0.2 Iris-setosa
9 4.9 3.1 1.5 0.1 Iris-setosa
10 5.4 3.7 1.5 0.2 Iris-setosa
11 4.8 3.4 1.6 0.2 Iris-setosa
12 4.8 3.0 1.4 0.1 Iris-setosa
13 4.3 3.0 1.1 0.1 Iris-setosa
14 5.8 4.0 1.2 0.2 Iris-setosa
15 5.7 4.4 1.5 0.4 Iris-setosa
16 5.4 3.9 1.3 0.4 Iris-setosa
17 5.1 3.5 1.4 0.3 Iris-setosa
18 5.7 3.8 1.7 0.3 Iris-setosa
19 5.1 3.8 1.5 0.3 Iris-setosa
20 5.4 3.4 1.7 0.2 Iris-setosa
21 5.1 3.7 1.5 0.4 Iris-setosa
22 4.6 3.6 1.0 0.2 Iris-setosa
23 5.1 3.3 1.7 0.5 Iris-setosa
24 4.8 3.4 1.9 0.2 Iris-setosa
25 5.0 3.0 1.6 0.2 Iris-setosa
26 5.0 3.4 1.6 0.4 Iris-setosa
27 5.2 3.5 1.5 0.2 Iris-setosa
28 5.2 3.4 1.4 0.2 Iris-setosa
29 4.7 3.2 1.6 0.2 Iris-setosa
30 4.8 3.1 1.6 0.2 Iris-setosa
31 5.4 3.4 1.5 0.4 Iris-setosa
32 5.2 4.1 1.5 0.1 Iris-setosa
33 5.5 4.2 1.4 0.2 Iris-setosa
34 4.9 3.1 1.5 0.1 Iris-setosa
35 5.0 3.2 1.2 0.2 Iris-setosa
36 5.5 3.5 1.3 0.2 Iris-setosa
37 4.9 3.1 1.5 0.1 Iris-setosa
38 4.4 3.0 1.3 0.2 Iris-setosa
39 5.1 3.4 1.5 0.2 Iris-setosa
40 5.0 3.5 1.3 0.3 Iris-setosa
41 4.5 2.3 1.3 0.3 Iris-setosa
42 4.4 3.2 1.3 0.2 Iris-setosa
43 5.0 3.5 1.6 0.6 Iris-setosa
44 5.1 3.8 1.9 0.4 Iris-setosa
45 4.8 3.0 1.4 0.3 Iris-setosa
46 5.1 3.8 1.6 0.2 Iris-setosa
47 4.6 3.2 1.4 0.2 Iris-setosa
48 5.3 3.7 1.5 0.2 Iris-setosa
49 5.0 3.3 1.4 0.2 Iris-setosa
Iris_versicolor_dataframe is
Sepal.Length Sepal.Width Petal.Length Petal.Width Category
50 7.0 3.2 4.7 1.4 Iris-versicolor
51 6.4 3.2 4.5 1.5 Iris-versicolor
52 6.9 3.1 4.9 1.5 Iris-versicolor
53 5.5 2.3 4.0 1.3 Iris-versicolor
54 6.5 2.8 4.6 1.5 Iris-versicolor
55 5.7 2.8 4.5 1.3 Iris-versicolor
56 6.3 3.3 4.7 1.6 Iris-versicolor
57 4.9 2.4 3.3 1.0 Iris-versicolor
58 6.6 2.9 4.6 1.3 Iris-versicolor
59 5.2 2.7 3.9 1.4 Iris-versicolor
60 5.0 2.0 3.5 1.0 Iris-versicolor
61 5.9 3.0 4.2 1.5 Iris-versicolor
62 6.0 2.2 4.0 1.0 Iris-versicolor
63 6.1 2.9 4.7 1.4 Iris-versicolor
64 5.6 2.9 3.6 1.3 Iris-versicolor
65 6.7 3.1 4.4 1.4 Iris-versicolor
66 5.6 3.0 4.5 1.5 Iris-versicolor
67 5.8 2.7 4.1 1.0 Iris-versicolor
68 6.2 2.2 4.5 1.5 Iris-versicolor
69 5.6 2.5 3.9 1.1 Iris-versicolor
70 5.9 3.2 4.8 1.8 Iris-versicolor
71 6.1 2.8 4.0 1.3 Iris-versicolor
72 6.3 2.5 4.9 1.5 Iris-versicolor
73 6.1 2.8 4.7 1.2 Iris-versicolor
74 6.4 2.9 4.3 1.3 Iris-versicolor
75 6.6 3.0 4.4 1.4 Iris-versicolor
76 6.8 2.8 4.8 1.4 Iris-versicolor
77 6.7 3.0 5.0 1.7 Iris-versicolor
78 6.0 2.9 4.5 1.5 Iris-versicolor
79 5.7 2.6 3.5 1.0 Iris-versicolor
80 5.5 2.4 3.8 1.1 Iris-versicolor
81 5.5 2.4 3.7 1.0 Iris-versicolor
82 5.8 2.7 3.9 1.2 Iris-versicolor
83 6.0 2.7 5.1 1.6 Iris-versicolor
84 5.4 3.0 4.5 1.5 Iris-versicolor
85 6.0 3.4 4.5 1.6 Iris-versicolor
86 6.7 3.1 4.7 1.5 Iris-versicolor
87 6.3 2.3 4.4 1.3 Iris-versicolor
88 5.6 3.0 4.1 1.3 Iris-versicolor
89 5.5 2.5 4.0 1.3 Iris-versicolor
90 5.5 2.6 4.4 1.2 Iris-versicolor
91 6.1 3.0 4.6 1.4 Iris-versicolor
92 5.8 2.6 4.0 1.2 Iris-versicolor
93 5.0 2.3 3.3 1.0 Iris-versicolor
94 5.6 2.7 4.2 1.3 Iris-versicolor
95 5.7 3.0 4.2 1.2 Iris-versicolor
96 5.7 2.9 4.2 1.3 Iris-versicolor
97 6.2 2.9 4.3 1.3 Iris-versicolor
98 5.1 2.5 3.0 1.1 Iris-versicolor
99 5.7 2.8 4.1 1.3 Iris-versicolor
Iris_virginica_dataframe is
Sepal.Length Sepal.Width Petal.Length Petal.Width Category
100 6.3 3.3 6.0 2.5 Iris-virginica
101 5.8 2.7 5.1 1.9 Iris-virginica
102 7.1 3.0 5.9 2.1 Iris-virginica
103 6.3 2.9 5.6 1.8 Iris-virginica
104 6.5 3.0 5.8 2.2 Iris-virginica
105 7.6 3.0 6.6 2.1 Iris-virginica
106 4.9 2.5 4.5 1.7 Iris-virginica
107 7.3 2.9 6.3 1.8 Iris-virginica
108 6.7 2.5 5.8 1.8 Iris-virginica
109 7.2 3.6 6.1 2.5 Iris-virginica
110 6.5 3.2 5.1 2.0 Iris-virginica
111 6.4 2.7 5.3 1.9 Iris-virginica
112 6.8 3.0 5.5 2.1 Iris-virginica
113 5.7 2.5 5.0 2.0 Iris-virginica
114 5.8 2.8 5.1 2.4 Iris-virginica
115 6.4 3.2 5.3 2.3 Iris-virginica
116 6.5 3.0 5.5 1.8 Iris-virginica
117 7.7 3.8 6.7 2.2 Iris-virginica
118 7.7 2.6 6.9 2.3 Iris-virginica
119 6.0 2.2 5.0 1.5 Iris-virginica
120 6.9 3.2 5.7 2.3 Iris-virginica
121 5.6 2.8 4.9 2.0 Iris-virginica
122 7.7 2.8 6.7 2.0 Iris-virginica
123 6.3 2.7 4.9 1.8 Iris-virginica
124 6.7 3.3 5.7 2.1 Iris-virginica
125 7.2 3.2 6.0 1.8 Iris-virginica
126 6.2 2.8 4.8 1.8 Iris-virginica
127 6.1 3.0 4.9 1.8 Iris-virginica
128 6.4 2.8 5.6 2.1 Iris-virginica
129 7.2 3.0 5.8 1.6 Iris-virginica
130 7.4 2.8 6.1 1.9 Iris-virginica
131 7.9 3.8 6.4 2.0 Iris-virginica
132 6.4 2.8 5.6 2.2 Iris-virginica
133 6.3 2.8 5.1 1.5 Iris-virginica
134 6.1 2.6 5.6 1.4 Iris-virginica
135 7.7 3.0 6.1 2.3 Iris-virginica
136 6.3 3.4 5.6 2.4 Iris-virginica
137 6.4 3.1 5.5 1.8 Iris-virginica
138 6.0 3.0 4.8 1.8 Iris-virginica
139 6.9 3.1 5.4 2.1 Iris-virginica
140 6.7 3.1 5.6 2.4 Iris-virginica
141 6.9 3.1 5.1 2.3 Iris-virginica
142 5.8 2.7 5.1 1.9 Iris-virginica
143 6.8 3.2 5.9 2.3 Iris-virginica
144 6.7 3.3 5.7 2.5 Iris-virginica
145 6.7 3.0 5.2 2.3 Iris-virginica
146 6.3 2.5 5.0 1.9 Iris-virginica
147 6.5 3.0 5.2 2.0 Iris-virginica
148 6.2 3.4 5.4 2.3 Iris-virginica
149 5.9 3.0 5.1 1.8 Iris-virginica
4.2 第二步数据集按照测试集和训练集分类
人为规定训练集占比 0.7,数据集为 0.3 下面将定义一个名为 get_train_and_test_dataframe 的函数,并返回训练集和测试集的 DataFrame。
In[2]:
total_record, attribute_rows = df.shape # 获取总记录条数和其属性列
train_data_rate =0.7# 训练集占数据集的比例,即70%
test_data_rate =1- train_data_rate # 测试集与训练集为互补集defget_train_and_test_dataframe(df1, df2, df3, train_data_rate):
train_df = pd.DataFrame()# 创建一个空的dataframe
test_df = pd.DataFrame()# 创建一个空的dataframe
df_array =[df1, df2, df3]# 将各个df子集存入一个列表用于变量for i inrange(3):
item_df_record_num, _ = df_array[i].shape # 获取每个df子集的记录总条数
item_df_train_record_num =int(item_df_record_num* train_data_rate)# 计算每个df子集的训练数据总记录条数# 随机从df子集中抽取数量为 itemDf_trainRecordNum 的记录作为训练集
train_records = df_array[i].sample(item_df_train_record_num)# 子集中除去被选出为测试集的其余记录作为测试集
test_records = df_array[i][~df_array[i].index.isin(train_records.index)]# 将每个子集中的训练集添加到trainDf中
train_df = pd.concat([train_df, train_records])# 将每个子集中的测试集添加到testDf中
test_df = pd.concat([test_df, test_records])return train_df, test_df
In[3]:
train_data, test_data = get_train_and_test_dataframe(Iris_setosa_dataframe, Iris_versicolor_dataframe, Iris_virginica_dataframe, train_data_rate)print(train_data)print(test_data)
out[3]:
Sepal.Length Sepal.Width Petal.Length Petal.Width Category
31 5.4 3.4 1.5 0.4 Iris-setosa
12 4.8 3.0 1.4 0.1 Iris-setosa
6 4.6 3.4 1.4 0.3 Iris-setosa
25 5.0 3.0 1.6 0.2 Iris-setosa
13 4.3 3.0 1.1 0.1 Iris-setosa
.. … … … … …
132 6.4 2.8 5.6 2.2 Iris-virginica
138 6.0 3.0 4.8 1.8 Iris-virginica
141 6.9 3.1 5.1 2.3 Iris-virginica
120 6.9 3.2 5.7 2.3 Iris-virginica
143 6.8 3.2 5.9 2.3 Iris-virginica
[105 rows x 5 columns]
Sepal.Length Sepal.Width Petal.Length Petal.Width Category
1 4.9 3.0 1.4 0.2 Iris-setosa
8 4.4 2.9 1.4 0.2 Iris-setosa
14 5.8 4.0 1.2 0.2 Iris-setosa
15 5.7 4.4 1.5 0.4 Iris-setosa
17 5.1 3.5 1.4 0.3 Iris-setosa
20 5.4 3.4 1.7 0.2 Iris-setosa
24 4.8 3.4 1.9 0.2 Iris-setosa
29 4.7 3.2 1.6 0.2 Iris-setosa
34 4.9 3.1 1.5 0.1 Iris-setosa
35 5.0 3.2 1.2 0.2 Iris-setosa
37 4.9 3.1 1.5 0.1 Iris-setosa
38 4.4 3.0 1.3 0.2 Iris-setosa
42 4.4 3.2 1.3 0.2 Iris-setosa
43 5.0 3.5 1.6 0.6 Iris-setosa
45 4.8 3.0 1.4 0.3 Iris-setosa
50 7.0 3.2 4.7 1.4 Iris-versicolor
57 4.9 2.4 3.3 1.0 Iris-versicolor
58 6.6 2.9 4.6 1.3 Iris-versicolor
59 5.2 2.7 3.9 1.4 Iris-versicolor
61 5.9 3.0 4.2 1.5 Iris-versicolor
65 6.7 3.1 4.4 1.4 Iris-versicolor
68 6.2 2.2 4.5 1.5 Iris-versicolor
70 5.9 3.2 4.8 1.8 Iris-versicolor
75 6.6 3.0 4.4 1.4 Iris-versicolor
77 6.7 3.0 5.0 1.7 Iris-versicolor
80 5.5 2.4 3.8 1.1 Iris-versicolor
83 6.0 2.7 5.1 1.6 Iris-versicolor
86 6.7 3.1 4.7 1.5 Iris-versicolor
87 6.3 2.3 4.4 1.3 Iris-versicolor
90 5.5 2.6 4.4 1.2 Iris-versicolor
100 6.3 3.3 6.0 2.5 Iris-virginica
102 7.1 3.0 5.9 2.1 Iris-virginica
105 7.6 3.0 6.6 2.1 Iris-virginica
106 4.9 2.5 4.5 1.7 Iris-virginica
112 6.8 3.0 5.5 2.1 Iris-virginica
116 6.5 3.0 5.5 1.8 Iris-virginica
121 5.6 2.8 4.9 2.0 Iris-virginica
127 6.1 3.0 4.9 1.8 Iris-virginica
129 7.2 3.0 5.8 1.6 Iris-virginica
133 6.3 2.8 5.1 1.5 Iris-virginica
135 7.7 3.0 6.1 2.3 Iris-virginica
136 6.3 3.4 5.6 2.4 Iris-virginica
142 5.8 2.7 5.1 1.9 Iris-virginica
146 6.3 2.5 5.0 1.9 Iris-virginica
148 6.2 3.4 5.4 2.3 Iris-virginica
4.3 第三步定义简单的概率估算方法
4.3.1 简介
类似 KNN,但是这个更为简单并且是一维的,它基于给定的数据集
X
X
X,对于一个新的数据点
x
0
x_0
x0,通过计算其与数据集中已有数据点的距离,然后根据最近邻的距离来估算其属于数据集的
概率。
4.3.2 作用
求贝叶斯分类公式中的
P
(
E
1
∣
H
i
)
P(E_1|H_i)
P(E1∣Hi),也就是当为前提
H
i
H_i
Hi 的情况下,
E
=
E
i
E= E_i
E=Ei 的概率。
在该题目中的含义为求当类别为
C
i
C_i
Ci 的前提下,某一个属性列
A
1
A_1
A1 的值为
a
1
a_1
a1的概率,也就是
P
(
A
=
a
i
∣
C
i
)
P(A=a_i|C_i)
P(A=ai∣Ci)
4.3.3 接口说明
需要传入下面几个参数:
X X X: 训练集的数据集x 0 x_0 x0: 测试集中的一个属性列的值- plot_graph: 是否需要生成图片
- epsilon: 控制误差的系数
4.3.4 返回参数说明
- plot_graph 默认为 False,若在调用时不设置为 True 则不返回图片
- 返回 probability 为 x 0 x_0 x0 属于 X X X 的概率
4.3.5 代码部分
In[4]:
"""
下面这个是一个简单的概率估算方法,它基于给定的数据集 X,
对于一个新的数据点 x0,通过计算其与数据集中已有数据点的距离,
然后根据最近邻的距离来估算其属于数据集的概率。
具体来说,函数 estimate_probability 中的
calculate_probability 函数计算了数据点 x0 与数据集中每个点的距离,
并找到最近距离 min_distance。然后,计算落在与最近距离接近的范围内的点的个数,
并通过除以总数据点数来估算概率。
"""import numpy as np
import matplotlib.pyplot as plt
defestimate_probability(X, x0, plot_graph=False, epsilon=1e-3):# 计算两点之间的距离defdistance(x1, x2):returnabs(x1 - x2)# 估算x0属于数据集的概率defcalculate_probability(X, x0, epsilon):
distances =[distance(x, x0)for x in X]
min_distance = np.min(distances)
count =sum(1for d in distances ifabs(d - min_distance)< epsilon)
probability = count /len(X)return probability
# 计算单个x0值的概率
probability = calculate_probability(X, x0, epsilon)# 是否需要显示图片if plot_graph:
x_values = np.linspace(min(X),max(X),100)
probabilities =[calculate_probability(X, point, epsilon)for point in x_values]
plt.plot(x_values, probabilities)
plt.xlabel("X = x0")# 设置x标签
plt.ylabel("Probability of belonging to the data set")# 设置y标签
plt.title("The probability that a new data point belongs to the data set")# 设置标题
plt.grid(True)
plt.axvline(x=x0, color='red', linestyle='--', label=f"x0 = {x0}")
plt.legend()
plt.show()return probability
4.4 第四步定义贝叶斯公式
4.4.1 背景
- 设所属类别为 C i C_i Ci,共有三种类别 Iris-setosa、Iris-versicolor、Iris-virginica,分别为 C 1 C_1 C1、 C 2 C_2 C2、 C 3 C_3 C3。
- 此外还有四个属性 A i A_i Ai,共有四个属性 Sepal.Length、Sepal.Width、Petal.Length、Petal.Width,分别为 A 1 A_1 A1、 A 2 A_2 A2、 A 3 A_3 A3、 A 4 A_4 A4。
4.4.2 公式原型(假设论据间条件独立)
P
(
C
i
∣
A
1
=
a
1
,
A
2
=
a
2
,
A
3
=
a
3
,
A
4
=
a
4
)
=
P
(
A
1
=
a
1
∣
C
i
)
∗
P
(
A
2
=
a
2
∣
C
i
)
∗
P
(
A
3
=
a
3
∣
C
i
)
∗
P
(
A
4
=
a
4
∣
C
i
)
∗
P
(
C
i
)
∑
i
=
1
3
P
(
A
1
=
a
1
∣
C
i
)
∗
P
(
A
2
=
a
2
∣
C
i
)
∗
P
(
A
3
=
a
3
∣
C
i
)
∗
P
(
A
4
=
a
4
∣
C
i
)
∗
P
(
C
i
)
P(C_i|A_1=a_1,A_2=a_2,A_3=a_3,A_4=a_4) = \frac {P(A_1=a_1|C_i) * P(A_2=a_2|C_i) * P(A_3=a_3|C_i) * P(A_4=a_4|C_i) * P(C_i) } {\sum_{i = 1}^{3} P(A_1=a_1|C_i) * P(A_2=a_2|C_i) * P(A_3=a_3|C_i) * P(A_4=a_4|C_i) * P(C_i)}
P(Ci∣A1=a1,A2=a2,A3=a3,A4=a4)=∑i=13P(A1=a1∣Ci)∗P(A2=a2∣Ci)∗P(A3=a3∣Ci)∗P(A4=a4∣Ci)∗P(Ci)P(A1=a1∣Ci)∗P(A2=a2∣Ci)∗P(A3=a3∣Ci)∗P(A4=a4∣Ci)∗P(Ci)
4.4.3 化简公式
- 因为预测一个测试记录所属类别需要按照 C i = C 1 , C 2 , C 3 C_i = C_1, C_2, C_3 Ci=C1,C2,C3代入上述公式,并且比较其大小,概率较大的为最可能的类别。
- 由观察可知分母都相同,因此只需要比较分子即可,也就是比较 P ( A 1 = a 1 ∣ C i ) × P ( A 2 = a 2 ∣ C i ) × P ( A 3 = a 3 ∣ C i ) × P ( A 4 = a 4 ∣ C i ) × P ( C i ) P(A_1=a_1|C_i) ×P(A_2=a_2|C_i) × P(A_3=a_3|C_i) × P(A_4=a_4|C_i) × P(C_i) P(A1=a1∣Ci)×P(A2=a2∣Ci)×P(A3=a3∣Ci)×P(A4=a4∣Ci)×P(Ci)。
- 每一个 P ( A i = a i ∣ C i ) P(A_i = a_i | C_i) P(Ai=ai∣Ci)只需要调用上面
estimate_probability函数即可
4.4.4 传入参数说明
传入record是指每条测试记录,类型为pandas.Series
4.4.5 返回参数说明
return p_category
是指返回该测试记录所属类别概率的一个字典,key为类型名称,value为对应类型的概率。
4.4.6 代码部分
In[5]:
# 贝叶斯分类defbayesian_classification(record):
attribute_index =0# 当前所在属性列的第几个
total_attributes =len(record)# 一共有多少个属性列
category =["Iris-setosa","Iris-versicolor","Iris-virginica"]# 每次调用贝叶斯分类时都初始化所属类别的概率
p_category ={"Iris-setosa":1.0,# 该记录属于setosa的概率,1即为100%"Iris-versicolor":1.0,# 该记录属于versicolor的概率"Iris-virginica":1.0# 该记录属于virginica的概率}for category_item in category:# 对每个种类进行判别属于改种类的概论
attribute_index =0# 每次进行类型循环时就重置属性列的索引,重新从1开始# 通过categoryItem来进行训练集的筛选if category_item =="Iris-setosa":
train_data_item = train_data.query(expr_1)elif category_item =="Iris-versicolor":
train_data_item = train_data.query(expr_2)else:# category_item == "Iris-virginica":
train_data_item = train_data.query(expr_3)for attribute_row, value in record.items():# 遍历测试集里面的每个记录
attribute_index = attribute_index +1if attribute_index == total_attributes:
p_category[category_item]= p_category[category_item]/3# P(Ci)的值,因为每个种类的数量都一样所以是1/3else:# 某个种类中某个属性的训练集
train_attribute_set = np.array(train_data_item[attribute_row])# 测试集中某个属性的值
test_attribute = value
# 调用简单概率估算函数并获取概率
probability = estimate_probability(train_attribute_set, test_attribute, plot_graph=False)
p_category[category_item]= p_category[category_item]* probability
return p_category
4.5 第五步定义验证和打印函数
4.5.1 简介
verify
函数是每次循环测试记录时需要调用的,可以用来打印结果和验证是否预测正确。
4.5.2 入口参数说明
- index:测试记录在数据集中的索引
- p_catagory:该测试记录经过贝叶斯分类后返回的结果(属于各类别的概率)
- real_category:该测试记录真实所属类别
- record_num:已经遍历测试记录的数量
- correct_num:已经遍历测试记录并且预测结果为正确的数量
- correct_rate:该模型的正确率
4.5.3 返回参数说明
- correct_num:同上
- correct_rate:同上
4.5.4 代码部分
In[6]:
defverify(index, p_catagory, real_category, record_num, correct_num, correct_rate):print("测试结果已出,该测试记录所属类别的概率为\n",p_category)# 打印该记录所对应类别的概率
max_probability =max(p_category.values())# 获取最大的概率值for key, key_value in p_category.items():# 寻找概率最大的类别if key_value == max_probability:## 找到概率最大的类别print(f"第{index}记录的预测最可能的所属类别为:{key}")print(f"第{index}记录的真实属性为:{real_category}")if key == real_category:## 查看预测的类别和真实的类别是否一样
correct_num = correct_num +1# 若一样则correct_num++print("-------------------------")
correct_rate = correct_num / record_num # 计算新的正确率return correct_num, correct_rate
4.6 第六步开始对测试集中的记录进行贝叶斯分类
In[7]:
correct_rate =0# 准确率
correct_num =0# 准确条数
record_num =0# 记录条数for index, record in test_data.iterrows():# 遍历测试集
record_num = record_num +1# 遍历的测试记录条数++print(f"记录 {index}:")
p_category = bayesian_classification(record)# 调用贝叶斯分类函数
correct_num, correct_rate = verify(index, p_category, record["Category"], record_num, correct_num, correct_rate)# 更新正确条数和正确率print(f"该模型的预测准确率为:{correct_rate}")
out[7]:
记录 1:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 0.0001012911286963765, 'Iris-versicolor':
1.3327780091628485e-05, 'Iris-virginica': 2.221296681938081e-06}
第 1 记录的预测最可能的所属类别为:Iris-setosa
第 1 记录的真实属性为:Iris-setosa
-------------------------
记录 8:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 0.000202582257392753, 'Iris-versicolor':
1.5993336109954184e-05, 'Iris-virginica': 8.885186727752324e-07}
第 8 记录的预测最可能的所属类别为:Iris-setosa
第 8 记录的真实属性为:Iris-setosa
-------------------------
记录 14:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 7.596834652228237e-05, 'Iris-versicolor':
3.998334027488546e-06, 'Iris-virginica': 1.7770373455504648e-06}
第 14 记录的预测最可能的所属类别为:Iris-setosa
第 14 记录的真实属性为:Iris-setosa
-------------------------
记录 15:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 1.4660558100791335e-05, 'Iris-versicolor':
6.663890045814243e-06, 'Iris-virginica': 8.885186727752324e-07}
第 15 记录的预测最可能的所属类别为:Iris-setosa
第 15 记录的真实属性为:Iris-setosa
-------------------------
记录 17:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 0.0002487852283770651, 'Iris-versicolor':
1.3327780091628486e-06, 'Iris-virginica': 4.442593363876162e-07}
第 17 记录的预测最可能的所属类别为:Iris-setosa
第 17 记录的真实属性为:Iris-setosa
-------------------------
记录 20:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 0.0003545189504373177, 'Iris-versicolor':
1.3327780091628486e-06, 'Iris-virginica': 8.885186727752324e-07}
第 20 记录的预测最可能的所属类别为:Iris-setosa
第 20 记录的真实属性为:Iris-setosa
-------------------------
记录 24:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 8.862973760932943e-05, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 8.885186727752324e-07}
第 24 记录的预测最可能的所属类别为:Iris-setosa
第 24 记录的真实属性为:Iris-setosa
-------------------------
记录 29:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 4.220463695682353e-05, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 2.221296681938081e-06}
第 29 记录的预测最可能的所属类别为:Iris-setosa
第 29 记录的真实属性为:Iris-setosa
-------------------------
记录 34:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.932111620158267e-05, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 1.7770373455504648e-06}
第 34 记录的预测最可能的所属类别为:Iris-setosa
第 34 记录的真实属性为:Iris-setosa
-------------------------
记录 35:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 0.0003038733860891295, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 2.221296681938081e-06}
第 35 记录的预测最可能的所属类别为:Iris-setosa
第 35 记录的真实属性为:Iris-setosa
-------------------------
记录 37:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.932111620158267e-05, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 1.7770373455504648e-06}
第 37 记录的预测最可能的所属类别为:Iris-setosa
第 37 记录的真实属性为:Iris-setosa
-------------------------
记录 38:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 0.0001266139108704706, 'Iris-versicolor':
1.3327780091628485e-05, 'Iris-virginica': 2.221296681938081e-06}
第 38 记录的预测最可能的所属类别为:Iris-setosa
第 38 记录的真实属性为:Iris-setosa
-------------------------
记录 42:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 8.440927391364707e-05, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 2.221296681938081e-06}
第 42 记录的预测最可能的所属类别为:Iris-setosa
第 42 记录的真实属性为:Iris-setosa
-------------------------
记录 43:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.665556018325697e-05, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 4.442593363876162e-07}
第 43 记录的预测最可能的所属类别为:Iris-setosa
第 43 记录的真实属性为:Iris-setosa
-------------------------
记录 45:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 7.996668054977093e-05, 'Iris-versicolor':
1.3327780091628485e-05, 'Iris-virginica': 2.221296681938081e-06}
第 45 记录的预测最可能的所属类别为:Iris-setosa
第 45 记录的真实属性为:Iris-setosa
-------------------------
记录 50:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 4.442593363876162e-07, 'Iris-versicolor':
1.999167013744273e-06, 'Iris-virginica': 6.663890045814243e-06}
第 50 记录的预测最可能的所属类别为:Iris-virginica
第 50 记录的真实属性为:Iris-versicolor
-------------------------
记录 57:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.221296681938081e-07, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 8.885186727752324e-07}
第 57 记录的预测最可能的所属类别为:Iris-versicolor
第 57 记录的真实属性为:Iris-versicolor
-------------------------
记录 58:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
2.932111620158267e-05, 'Iris-virginica': 7.108149382201859e-06}
第 58 记录的预测最可能的所属类别为:Iris-versicolor
第 58 记录的真实属性为:Iris-versicolor
-------------------------
记录 59:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 1.999167013744273e-06, 'Iris-versicolor':
3.998334027488546e-06, 'Iris-virginica': 1.3327780091628486e-06}
第 59 记录的预测最可能的所属类别为:Iris-versicolor
第 59 记录的真实属性为:Iris-versicolor
-------------------------
记录 61:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
0.00013994169096209912, 'Iris-virginica': 2.221296681938081e-06}
第 61 记录的预测最可能的所属类别为:Iris-versicolor
第 61 记录的真实属性为:Iris-versicolor
-------------------------
记录 65:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
5.331112036651394e-06, 'Iris-virginica': 8.885186727752324e-06}
第 65 记录的预测最可能的所属类别为:Iris-virginica
第 65 记录的真实属性为:Iris-versicolor
-------------------------
记录 68:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.221296681938081e-07, 'Iris-versicolor':
9.329446064139942e-06, 'Iris-virginica': 4.442593363876162e-07}
第 68 记录的预测最可能的所属类别为:Iris-versicolor
第 68 记录的真实属性为:Iris-versicolor
-------------------------
记录 70:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 4.442593363876162e-07, 'Iris-versicolor':
2.665556018325697e-06, 'Iris-virginica': 1.9991670137442725e-05}
第 70 记录的预测最可能的所属类别为:Iris-virginica
第 70 记录的真实属性为:Iris-versicolor
-------------------------
记录 75:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
2.665556018325697e-05, 'Iris-virginica': 1.7770373455504647e-05}
第 75 记录的预测最可能的所属类别为:Iris-versicolor
第 75 记录的真实属性为:Iris-versicolor
-------------------------
记录 77:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.442593363876162e-06, 'Iris-virginica': 9.995835068721362e-05}
第 77 记录的预测最可能的所属类别为:Iris-virginica
第 77 记录的真实属性为:Iris-versicolor
-------------------------
记录 80:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 4.442593363876162e-07, 'Iris-versicolor':
3.998334027488546e-06, 'Iris-virginica': 8.885186727752324e-07}
第 80 记录的预测最可能的所属类别为:Iris-versicolor
第 80 记录的真实属性为:Iris-versicolor
-------------------------
记录 83:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
7.996668054977092e-06, 'Iris-virginica': 6.663890045814243e-06}
第 83 记录的预测最可能的所属类别为:Iris-versicolor
第 83 记录的真实属性为:Iris-versicolor
-------------------------
记录 86:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.664723032069971e-06, 'Iris-virginica': 8.885186727752324e-06}
第 86 记录的预测最可能的所属类别为:Iris-virginica
第 86 记录的真实属性为:Iris-versicolor
-------------------------
记录 87:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.221296681938081e-07, 'Iris-versicolor':
7.818964320422046e-05, 'Iris-virginica': 8.885186727752324e-07}
第 87 记录的预测最可能的所属类别为:Iris-versicolor
第 87 记录的真实属性为:Iris-versicolor
-------------------------
记录 90:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 4.442593363876162e-07, 'Iris-versicolor':
4.2648896293211154e-05, 'Iris-virginica': 8.885186727752324e-07}
第 90 记录的预测最可能的所属类别为:Iris-versicolor
第 90 记录的真实属性为:Iris-versicolor
-------------------------
记录 100:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 4.442593363876162e-07, 'Iris-versicolor':
1.7770373455504648e-06, 'Iris-virginica': 1.7770373455504648e-06}
第 100 记录的预测最可能的所属类别为:Iris-versicolor
第 100 记录的真实属性为:Iris-virginica
-------------------------
第 100 记录的预测最可能的所属类别为:Iris-virginica
第 100 记录的真实属性为:Iris-virginica
-------------------------
记录 102:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.442593363876162e-06, 'Iris-virginica': 6.663890045814243e-06}
第 102 记录的预测最可能的所属类别为:Iris-virginica
第 102 记录的真实属性为:Iris-virginica
-------------------------
记录 105:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.442593363876162e-06, 'Iris-virginica': 1.999167013744273e-05}
第 105 记录的预测最可能的所属类别为:Iris-virginica
第 105 记录的真实属性为:Iris-virginica
-------------------------
记录 106:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.221296681938081e-07, 'Iris-versicolor':
2.1324448146605577e-05, 'Iris-virginica': 7.996668054977092e-06}
第 106 记录的预测最可能的所属类别为:Iris-versicolor
第 106 记录的真实属性为:Iris-virginica
-------------------------
记录 112:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.442593363876162e-06, 'Iris-virginica': 3.3319450229071213e-06}
第 112 记录的预测最可能的所属类别为:Iris-versicolor
第 112 记录的真实属性为:Iris-virginica
-------------------------
记录 116:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.442593363876162e-06, 'Iris-virginica': 2.998750520616409e-05}
第 116 记录的预测最可能的所属类别为:Iris-virginica
第 116 记录的真实属性为:Iris-virginica
-------------------------
记录 121:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 1.999167013744273e-06, 'Iris-versicolor':
2.665556018325697e-05, 'Iris-virginica': 6.663890045814244e-06}
第 121 记录的预测最可能的所属类别为:Iris-versicolor
第 121 记录的真实属性为:Iris-virginica
-------------------------
记录 127:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
1.7770373455504647e-05, 'Iris-virginica': 9.995835068721363e-06}
第 127 记录的预测最可能的所属类别为:Iris-versicolor
第 127 记录的真实属性为:Iris-virginica
-------------------------
记录 129:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.442593363876162e-06, 'Iris-virginica': 4.442593363876162e-06}
第 129 记录的预测最可能的所属类别为:Iris-versicolor
第 129 记录的真实属性为:Iris-virginica
-------------------------
第 129 记录的预测最可能的所属类别为:Iris-virginica
第 129 记录的真实属性为:Iris-virginica
-------------------------
记录 133:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
3.731778425655977e-05, 'Iris-virginica': 1.3327780091628485e-05}
第 133 记录的预测最可能的所属类别为:Iris-versicolor
第 133 记录的真实属性为:Iris-virginica
-------------------------
记录 135:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
4.442593363876162e-06, 'Iris-virginica': 3.998334027488546e-05}
第 135 记录的预测最可能的所属类别为:Iris-virginica
第 135 记录的真实属性为:Iris-virginica
-------------------------
记录 136:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 1.554907677356657e-06, 'Iris-versicolor':
1.7770373455504648e-06, 'Iris-virginica': 8.885186727752324e-06}
第 136 记录的预测最可能的所属类别为:Iris-virginica
第 136 记录的真实属性为:Iris-virginica
-------------------------
记录 142:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 6.663890045814243e-07, 'Iris-versicolor':
7.996668054977092e-06, 'Iris-virginica': 1.999167013744273e-05}
第 142 记录的预测最可能的所属类别为:Iris-virginica
第 142 记录的真实属性为:Iris-virginica
-------------------------
记录 146:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 2.221296681938081e-07, 'Iris-versicolor':
7.108149382201859e-06, 'Iris-virginica': 5.331112036651394e-06}
第 146 记录的预测最可能的所属类别为:Iris-versicolor
第 146 记录的真实属性为:Iris-virginica
-------------------------
记录 148:
测试结果已出,该测试记录所属类别的概率为
{'Iris-setosa': 1.554907677356657e-06, 'Iris-versicolor':
8.885186727752324e-07, 'Iris-virginica': 2.665556018325697e-06}
第 148 记录的预测最可能的所属类别为:Iris-virginica
第 148 记录的真实属性为:Iris-virginica
-------------------------
该模型的预测准确率为:0.7555555555555555
4.7 测试index 为 2 的记录进行贝叶斯分类的过程
测试记录在数据集的 index 为 2,下面将会从三个类别出发,来判断该记录经过贝叶斯分类推断后所属哪个类别。
4.7.1 预测属于 Iris-setosa
- 该测试记录特征 Sepal.Length 的值属于 Iris-setosa 的概率图
- 该测试记录特征 Sepal.Width 的值属于 Iris-setosa 的概率图
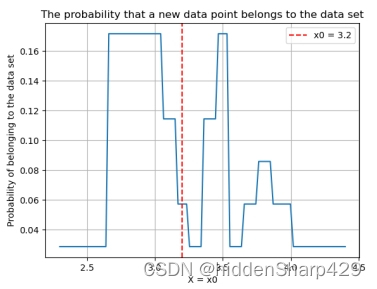
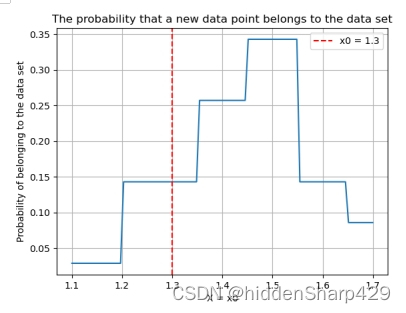
- 该测试记录特征 Petal.Length 的值属于 Iris-setosa 的概率图
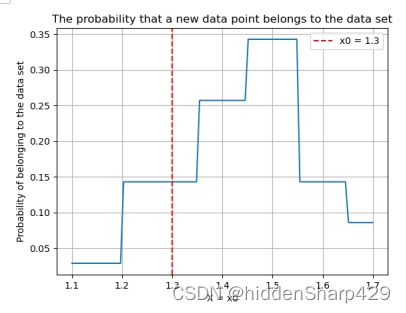
- 该测试记录特征 Petal.Width 的值属于 Iris-setosa 的概率图
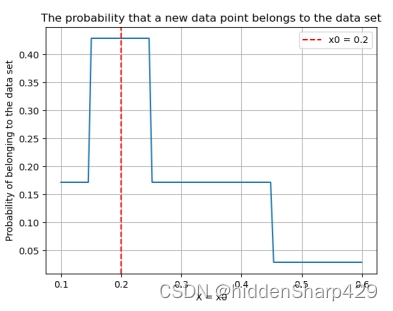
4.7.2 预测属于 Iris-versicolor
- 该测试记录特征 Sepal.Length 的值属于 Iris-versicolor 的概率图
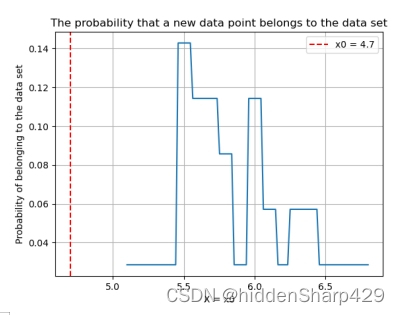
- 该测试记录特征 Sepal.Width 的值属于 Iris-versicolor 的概率图
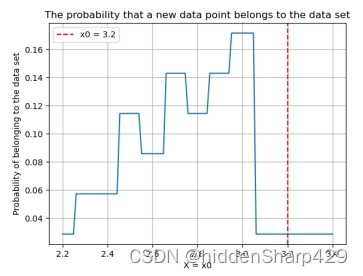
- 该测试记录特征 Petal.Length 的值属于 Iris-versicolor 的概率图
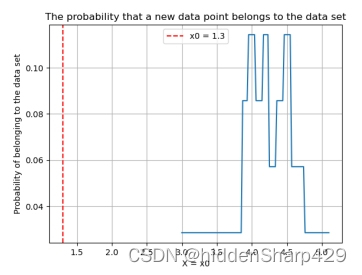
- 该测试记录特征 Petal.Width 的值属于 Iris-versicolor 的概率图
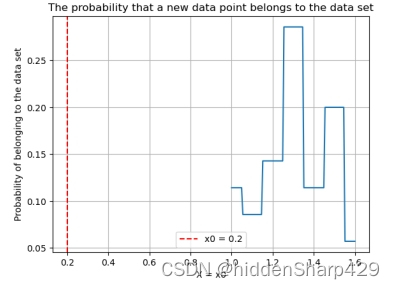
4.7.3 预测属于 Iris-virginica
- 该测试记录特征 Sepal.Length 的值属于 Iris-virginica 的概率图
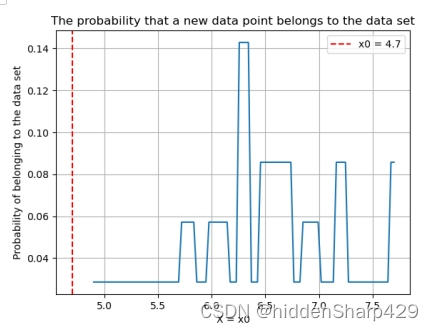
- 该测试记录特征 Sepal.Width 的值属于 Iris-virginica 的概率图
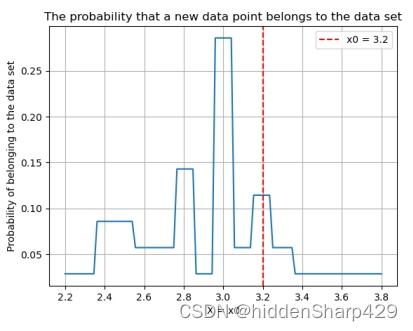
- 该测试记录特征 Petal.Length 的值属于 Iris-virginica 的概率图
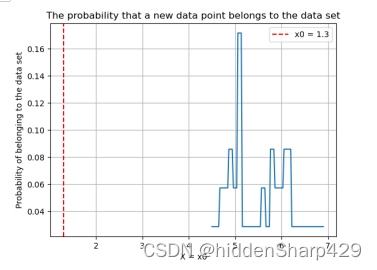
- 该测试记录特征 Petal.Width 的值属于 Iris-virginica 的概率图
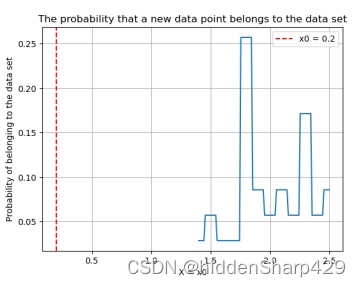
4.7.4 最后打印的结果
测试结果已出,该测试记录所属类别的概率为
’Iris-setosa’: 3.331945022907121e-05, ’Iris-versicolor’: 8.885186727752324e-07, ’Iris-virginica’:
8.885186727752324e-07
第 2 记录的预测最可能的所属类别为:Iris-setosa
第 2 记录的真实属性为:Iris-setosa
5. 结束语
如果有疑问欢迎大家留言讨论,你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗?我们之间的交流是我最大的动力!
版权归原作者 hiddenSharp429 所有, 如有侵权,请联系我们删除。