SI，SIS，SIR，SEIRD模型
因为个人工作需要系统地整理SI，SIR以及SEIR模型，故对三个模型进行原理介绍以及对比。文中关于SI，SIS，SIR的所有的截图都来自西工大肖华勇老师在慕课上的分享，原视频戳 这里。SEIRD模型则来自发表在SCI上的paper，想看原文戳这里。
SI model
作为比较古早的传染病模型（不对指数模型进行介绍），SI model在假设人口总数不变（不发生迁移，出生及死亡）的情况下，将人群分为易感人群S（suspectible）和病人I（Infective），在时刻
t
t
t下，这两类人群的占比分别为
s
(
t
)
s(t)
s(t)和
i
(
t
)
i(t)
i(t)，并假设病人每天有效接触的平均人数为
λ
\lambda
λ。当I类人群与S类人群进行接触，S被感染，转为I类人群。
So，每个病人每天可以感染的人数为
λ
⋅
s
(
t
)
\lambda \cdot s(t)
λ⋅s(t)，共有
N
⋅
i
(
t
)
N \cdot i(t)
N⋅i(t)个病人，故每天总感染人数为
λ
⋅
s
(
t
)
N
⋅
i
(
t
)
\lambda \cdot s(t) N \cdot i(t)
λ⋅s(t)N⋅i(t)
由图3可得，SI模型中新增病人数量在
i
=
1
/
2
i=1/2
i=1/2时增速最大，带入公式（6）可得
t
m
t_m
tm为该模型适用于不可治愈传染病。
SIS model
和SI模型不同，SIS模型假设病人治好后变成健康者，健康者可以再次被感染成为病人。相比与SI模型， SIS模型增加条件为：每天被治愈的病人数占病人总数的比例为一个常数
μ
\mu
μ，称
μ
\mu
μ为**日治愈率**，病人治愈后仍可被感染。
1
μ
\frac{1}{\mu}
μ1为平均感染期。如
μ
=
0.2
\mu = 0.2
μ=0.2时，该疾病的日治愈率为
20
%
20 \%
20%，平均感染期为5天。
得其增速曲线和函数曲线分别为
σ
>
1
\sigma>1
σ>1代表每天传染的人数大于治愈的人数，
σ
≤
1
\sigma \leq 1
σ≤1则相反。SIS的模型曲线表明，当每天传染的人数大于治愈人数时（
σ
>
1
\sigma>1
σ>1），不论初始状态下病人的人数是否大于
1
−
1
σ
1-\frac{1}{\sigma}
1−σ1，最终感染的人数都趋于定值；当
σ
≤
1
\sigma \leq 1
σ≤1时，所有人都会被治愈。显而易见，
σ
\sigma
σ在其中起关键作用。
SIR model
SIR考虑三种人群状态：S 类人群，易感人群；I 类人群，感染者；R 类人群，康复者，指的是感染者成功治愈，有免疫力的健康者。
由该图可得，SIR模型中病人最终全被治愈/移除，健康的易感者保持大于
5
%
5\%
5%的比例。该图由matlab绘制，具体参数如下：
其中病人初始占比为0.1，易感者为0.9。
在这里要说明的是，大部分论文在使用SIR模型时，传染率和治愈率是呈1.5倍的关系，即传染率比治愈率等于1.5，而治愈率由图中的拓扑结构决定，与肖老师在PPT中所展示的图有所不同。所以大部分论文在使用SIR模型时，得出的结论是图中感染者的数量最终会达到一个稳定状态（如下图所示），即趋于定值。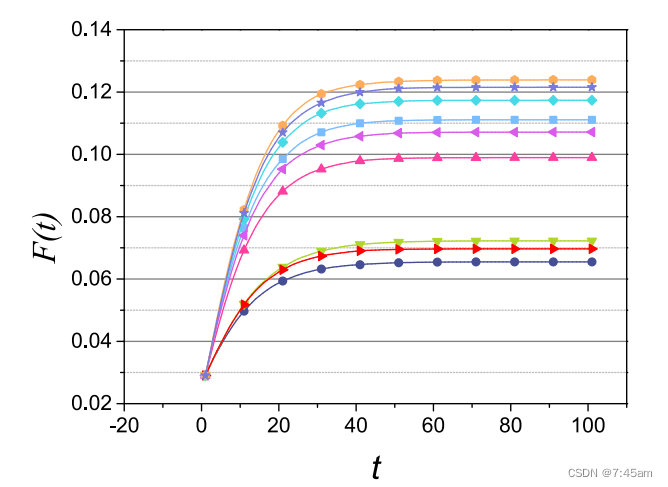
SEIRD model
受新冠疫情的启发，相对于SIR模型，该模型多了潜伏期（E），死亡（D）。
参数
γ
\gamma
γ反映了估计的病程时间,
γ
∈
[
1
18
,
1
5
]
\gamma \in [\frac{1}{18},\frac{1}{5}]
γ∈[181,51]。
参数
σ
\sigma
σ反映了该疾病的估计潜伏期,
σ
∈
[
1
5
,
1
3
]
\sigma\in[\frac{1}{5},\frac{1}{3}]
σ∈[51,31].
参数
β
\beta
β反映了感染者与他人互动的速率。它通常被写成
β
=
R
0
γ
\beta =R_0 \gamma
β=R0γ，其中
R
0
R_0
R0称为基本复制数，表示疾病的传染速度。Liu等人（2020）回顾了关于covid-19r0估计的文献，得出结论，文献中的平均和中位数估计约为3，但 在最新的文献中，有人认为5.7更合理。
参数
α
\alpha
α为infection fatality rate（IFR）死亡率，一般情况下
α
\alpha
α是变化的，在本文中作者认为
α
\alpha
α为定值。
参数
λ
\lambda
λ为真实报道中感染新冠病毒的人数占比，为定值。
模型初始化阶段为
D
(
0
)
=
0
,
R
(
0
)
=
0
,
C
(
0
)
=
0
,
S
(
0
)
=
N
−
E
(
0
)
−
I
(
0
)
−
R
(
0
)
−
D
(
0
)
=
N
−
E
(
0
)
−
I
(
0
)
D(0)=0,R(0)=0,C(0)=0,S(0)=N-E(0)-I(0)-R(0)-D(0)=N-E(0)-I(0)
D(0)=0,R(0)=0,C(0)=0,S(0)=N−E(0)−I(0)−R(0)−D(0)=N−E(0)−I(0)。
本文转载自: https://blog.csdn.net/qq_37730871/article/details/126532308
版权归原作者 7:45am 所有， 如有侵权，请联系我们删除。
版权归原作者 7:45am 所有， 如有侵权，请联系我们删除。