在本文中,我们将介绍熵、交叉熵和 Kullback-Leibler Divergence [2] 的概念,并了解如何将它们近似为相等。
尽管最初的建议使用 KL 散度,但在构建生成对抗网络 [1] 时,在损失函数中使用交叉熵是一种常见的做法。这常常给该领域的新手造成混乱。当我们有多个概率分布并且我们想比较它们之间的关系时,熵和 KL 散度的概念就会发挥作用。
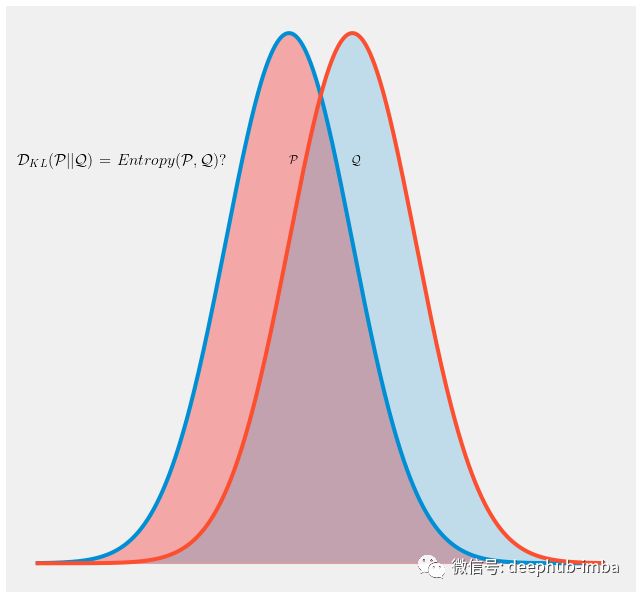
在这里我们将要验证为什么最小化交叉熵而不是使用 KL 散度会得到相同的输出。所以我们首先从正态分布中抽取两个概率分布 p 和 q。如图 1 所示,两种分布都不同,但是它们共享一个事实,即两者都是从正态分布中采样的。
熵
熵是系统不确定性的度量。直观地说它是从系统中消除不确定性所需的信息量。系统各种状态的概率分布 p 的熵可以计算如下:
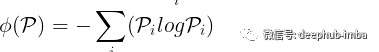
交叉熵
交叉熵是指存在于两个概率分布之间的信息量。在这种情况下,分布 p 和 q 的交叉熵可以表述如下:

KL散度
两个概率分布之间的散度是它们之间存在的距离的度量。概率分布 p 和 q 的KL散度( KL-Divergence )可以通过以下等式测量:
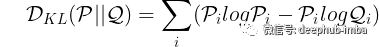
其中方程右侧的第一项是分布 p 的熵,第二项是分布 q 对 p 的期望。在大多数实际应用中,p 是实际数据/测量值,而 q 是假设分布。对于 GAN,p 是真实图像的概率分布,而 q 是生成的假图像的概率分布。
验证
现在让我们验证 KL 散度确实与使用交叉熵分布 p 和 q 相同。我们分别在 python 中计算熵、交叉熵和 KL 散度。
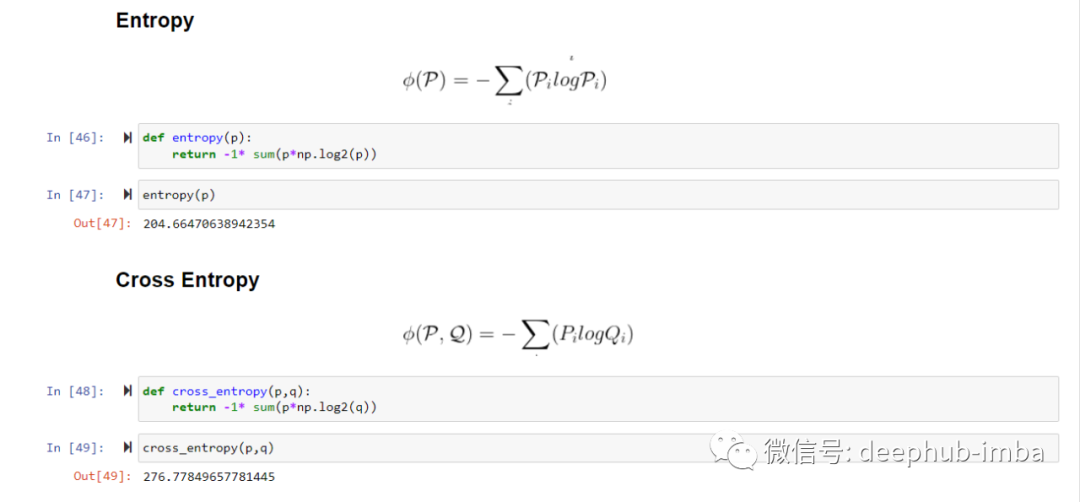
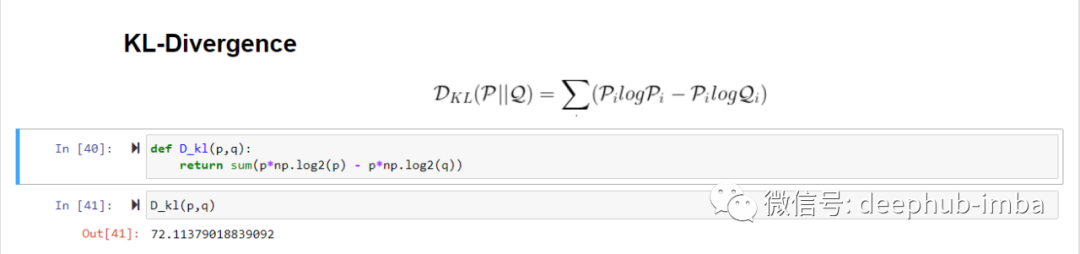

右侧的第二项,即分布 p 的熵可以被认为是一个常数,常数的导数是0,对反向传播不会有影响。因此我们可以得出结论,最小化交叉熵代替 KL 散度会出现相同的输出,因此可以近似相等。
总结
在本文中,我们了解了熵、交叉熵和 kl-散度的概念。然后我们回答了为什么这两个术语在深度学习应用程序中经常互换使用。我们还在 python 中实现并验证了这些概念。完整代码参考这个地址 https://github.com/azad-academy/kl_cross_entropy.git
引用
[1] Goodfellow, I. et al., Generative adversarial nets. In Advances in neural information processing systems. pp. 2672–2680, 2014
[2]https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence
作者:J. Rafid S., PhD