点赞、收藏必读文章--数据分析的多变量分析

数据探索性分析(EDA)——多(双)变量分析

0 引言

上一篇文章震惊！Python单变量分析竟然如此简单？
介绍了数据分析中的单变量分析，但是我们在实际场景中，遇到的数据大多数是具有多特征、多变量的，因此除了对单个变量进行分布、缺失等情况的探索，还需要对变量与变量之间的关系进行探索，因此今天小编就介绍一下多变量分析，而多变量分析本质上还是双变量的分析，所以小编会使用较大篇幅来进行双变量分析的介绍，再简单介绍一下多变量分析。

1 数据准备

本文中，小编在本地读取了一个实验所用的数据集，数据集没有业务含义，只用于方法的讲解。下图展示了数据的前10行，由此查看数据的大致情况：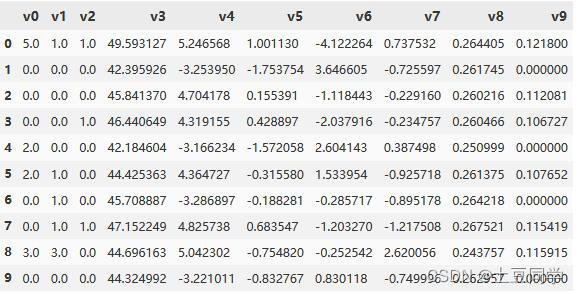

本次数据共有

v0~v9

共10个特征，其中

v0、v1、v2

是类别型变量，

 v3~v9

是连续型变量。

2 双变量分析

双变量分析目的是为了探索变量之间的关系，来更好地发现规律或者进行特征工程的建设。上文我们提到了变量可以分为连续型变量和类别型变量，因此根据变量类型的不同，双变量分析组合也可以分为三种：连续型与连续型、连续型与类别型、类别型与类别型。

2.1 连续型与连续型

连续型与连续型变量的分析主要有两种方法：回归分析和相关分析。其中回归分析主要的方法是散点图和回归曲线，相关分析主要是计算相关性以及绘制相关性热图。

(1) 回归分析

回归分析主要使用散点图+回归曲线进行观察，单独使用回归曲线用的比较少，因为在未知的情况下去观察回归曲线的话，并不一定能得到有效的结果，而散点图的形状可以更加容易直观地看出变量之间的关系是线性还是非线性，也能一定程度上判断出相关程度。所以这里我们用seaborn.regplot()方法绘制散点图来查看数据情况：

seaborn.regplot(x, y, data=None, ci=95, color=None, marker=’o’)

以下是是对几个常用参数的说明：

• x, y: 输入变量。格式为字符串、序列(series)或向量数组(vector array)。如果是字符串，应该与data中的列名相对应。 使用pandas对象时，轴将被Series的名字标记。
• data: 数据集，类型为DataFrame，其中每列为一个变量，每行为一个观测样本。
• color:(可选)用于选择绘图元素的颜色。
• marker:(可选)用于散点图的标记。
• ci:(可选) 位于[0, 100]之间的整数或None，表示回归估计的置信区间的大小。表现在图中为回归线周围的半透明带绘制。

下面就来实战一下，选择

v3、v4

列进行绘图：

sns.regplot(x ="v3", y ="v4", data = data, color='green', marker='*')   
plt.show()

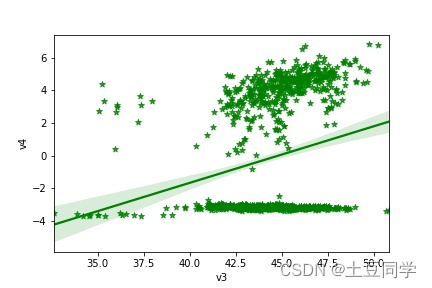
直线附近的阴影区域为回归估计的置信区间，

ci

取值越大，阴影区域越大。图中可以看到

v3、v4

线性关系并不强，散点图分布比较零散，没有呈现线状。

除了

sns.regplot()

方法，还有

sns.jointplot()

方法，用于绘制双变量联合分布图:

seaborn.jointplot(x,y,data=None,kind='scatter')

• x,y：分别记录x轴与y轴的数据名称
• data：数据集，数据类型为DataFrame
• kind：用于设置图形的类型，可选的类型有：scatter、reg、resid、kde、hex，分别表示散点图、回归图、残差图、核密度图和蜂巢图

还是以

v3、v4

列进行绘图：

sns.jointplot(x ="v3", y ="v4", data = data, kind='reg')
plt.show()

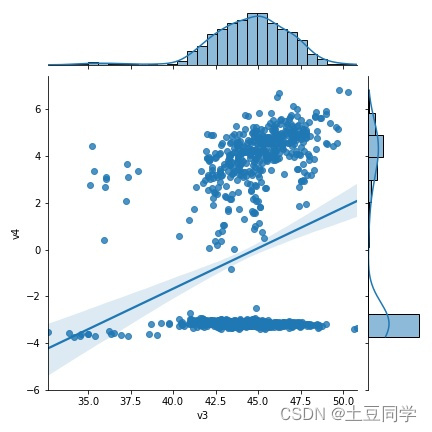
从图中就可以看到，

sns.jointplot()

其实就是在

sns.regplot()

图的上方和左侧再分别加上每个单变量的分布，单变量的分布在上一篇文章中有提到，可以用直方图和核密度图进行展示。

(2) 相关分析

散点图能比较直观地看出变量之间的关系，但是不能准确地量化变量之间的相关性，不能明确地反映变量关系的强弱。因为我们就可以用相关性来弥补散点图的缺陷，对变量之间的关系进行量化分析。

相关性系数

(Correlation)

的取值范围为

[-1, 1]

，当

Corr=1

时，说明两个变量强正线性相关；当

Corr=0

时，说明两个变量不相关；当

Corr=-1

时，说明两个变量强负线性相关。当然，我们在实践的时候，并不会单纯把变量的相关性分为以上三种，而是会把相关性取绝对值，再分别定义为无相关性

(0-0.1)

、弱相关

(0.1-0.3)

、中等相关

(0.3-0.5)

、强相关

(0.5-1)

，其中，除了无相关性，其他三种又可以分为正负两类。

对于相关性的计算，

Python

中有多种方法可以计算，比如

NumPy

包 的

np.corrcoef()

、

Scipy

包的

scipy.stats.pearsonr(x, y) 、scipy.stats.spearmanr(x, y)

，还有就是

pandas

的

x.corr(y)

，由于在平常数据分析用到

pandas

居多，所以小编这里就讲一下

pandas

：

data['v3'].corr(data['v4'])

0.2289827482589131

可以看到

v3、v4

列的相关性为

0.229

，为弱相关。但是实际数据处理过程中，因为有多个特征，所以我们一般不会两个两个特征去分别计算相关性，我们可以直接以矩阵的形式计算出每一个特征与其他所有特征的相关性并以热图进行可视化，具体计算方法在后文会介绍。

2.2 连续型与类别型

分析连续型与类别型变量的关系的思想：观察对于类别型变量的不同类别，连续型变量的分布情况。这个思想可以通过小提琴图

(Violin Plot)

实现。小提琴图是箱型图与核密度估计图的结合，它显示了一个（或多个）分类变量多个属性上的定量数据的分布，从而可以比较这些分布。与箱形图不同，其中所有绘图单元都与实际数据点对应，小提琴图描述了基础数据分布的核密度估计。

seaborn.violinplot(x=None, y=None, hue=None, data=None)

• x, y, hue：数据或向量数据中的变量名称
• data：DataFrame、数组、数组列表

这里对参数的介绍比较简单，想进一步了解的读者可以移步官网。

前文提到了

v0、v1、v2

是类别型变量，所以小编就绘制

v0

和

v3

变量之间的小提琴图：

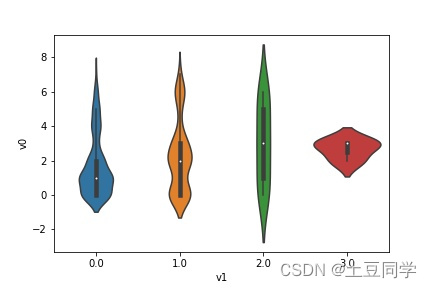
sns.violinplot(x ="v0", y ="v3", data = data)
plt.show()

可以看到，变量

v0

共有

0.0~7.0

八个类别，每个类别分别对应的

v3

变量的分布都不相同，由此可以对比在不同类别的情况下，连续变量

v0

的分布情况。

2.3 类别型与类别型

类别型变量之间也存在多种分析方法，如卡方检验、小提琴图、双向表、堆叠柱状图。本文中小编会介绍小提琴图以及卡方检验。

首先，绘制

v0

和

v1

变量之间的小提琴图：

卡方检验用于属于假设检验的一种，即比较理论频次与实际频次的吻合程度，这样可以分析变量的拟合程度，如拟合优度检验。由于我们的数据中没有对应的理论数据去检验相应的类别型变量，便不进行代码演示了。但是需要了解一下卡方检验的计算方法，可以用

scipy

包的

stats

模块中的

chisquare()

函数，又或者

sklearn

中的

chi2

方法。

3 多变量分析

有人可能疑问了，为啥把双变量单独列出来，双变量难道不属于多变量吗？其实双变量是属于多变量的，但是由于双变量分析的重要性，小编将双变量分析单独列出来讲解，多次的双变量分析就可以组成多变量分析，所以多变量分析实际上就是将多次的双变量分析工作集成在了一起。双变量分析用于你想了解两个变量的关系，此时其实你已经确实你需要分析哪两个变量了，而多变量分析可以用于你不知道哪些变量需要分析、哪些变量之间有相关性，则你就可以直接用一个多变量分析来观察哪些变量有相关性从而进行进一步的分析。

3.1 多连续型

在上面提到了可以用散点图观察变量之间是否存在线性关系，而

seaborn

中同样有方法

seaborn.pairplot()

可以以矩阵的形式呈现变量与其他所有变量之间的散点图，由于散点图比较适用于连续型变量之间，因此我们先把连续型变量选出来：

numeric_features =['v3','v4','v5','v6','v7','v8','v9']
data_numeric = data[numeric_features]

再用

seaborn.pairplot()

方法进行散点图矩阵可视化：

seaborn.pairplot(data,kind='scatter', diag_kind='auto')

• data：数据框架，其中每列是变量，每行是观察量。
• kind：(可选){‘scatter’, ‘reg’}。一种非等同关系的图类型。
• diag_kind：(可选){‘auto’, ‘hist’, ‘kde’}, 对角线子图的一种图形。

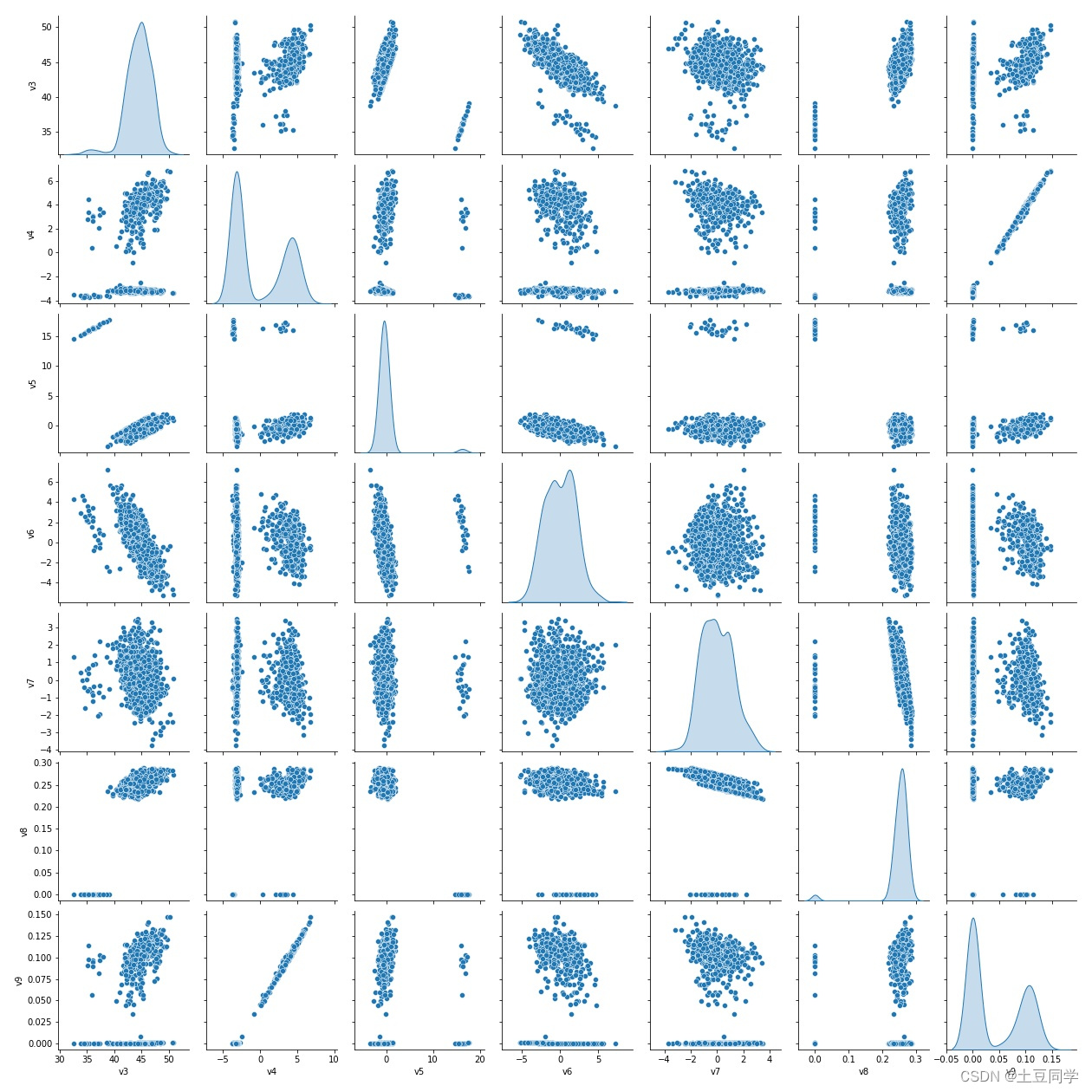
可以看到，整个矩阵中对角线呈现的是单个变量的核密度曲线，这个由

diag_kind

控制；其他的图都是某变量与其他变量的散点图，由

kind

控制。

pairplot()

图可以直接观察所有连续变量是否存在线性关系。

再计算连续型变量相关性并用热度图进行可视化：

correlation = data_numeric.corr()print(correlation)

          v3        v4        v5        v6        v7        v8        v9
v3  1.0000000.228983-0.385337-0.714666-0.2330400.6926920.230217
v4  0.2289831.0000000.0813980.007328-0.0177090.0473540.999474
v5 -0.3853370.0813981.000000-0.052123-0.046994-0.9099770.104331
v6 -0.7146660.007328-0.0521231.000000-0.020796-0.2003860.006363
v7 -0.233040-0.017709-0.046994-0.0207961.000000-0.230853-0.029284
v8  0.6926920.047354-0.909977-0.200386-0.2308531.0000000.031585
v9  0.2302170.9994740.1043310.006363-0.0292840.0315851.000000

然后再进行可视化，使用的方法为

seaborn.heatmap()

：

seaborn.heatmap(data, vmin=None, vmax=None, square=False)

• data：矩形数据集。可以强制转换为 ndarray 格式数据的 2 维数据集。如果提供了DataFrame 数据，索引/列信息将用于标记列和行。
• vmin, vmax：浮点型数据，可选参数。用于锚定色彩映射的值，否则它们是从数据和其他关键字参数推断出来的。
• square：布尔值，可选参数。如果为 True，则将坐标轴方向设置为“equal”，以使每个单元格为方形。

plt.figure(figsize =(7,7))
sns.heatmap(correlation,square =True)

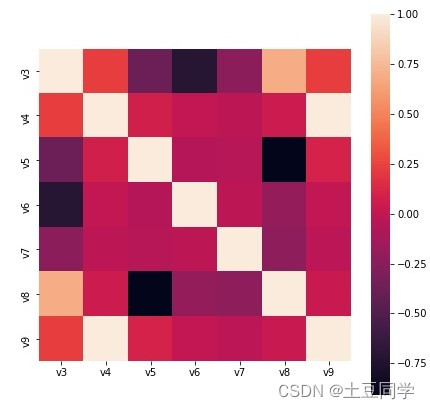
3.2 多类别型

多个类别型变量的观察不像连续型变量那样灵活，一般可以通过小提琴图或或者多柱状图进行可视化。

其中，多柱状图可以通过

seaborn.FacetGrid()

来绘制在同一个网格中，该方法用于绘制条件关系的多图网格，感兴趣的读者可以移步官网进行学习。

defcount_plot(x,**kwargs):
    sns.countplot(x=x)
f = pd.melt(data, value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable",  sharex=False, sharey=False, size=5)  
g = g.map(count_plot,"value")

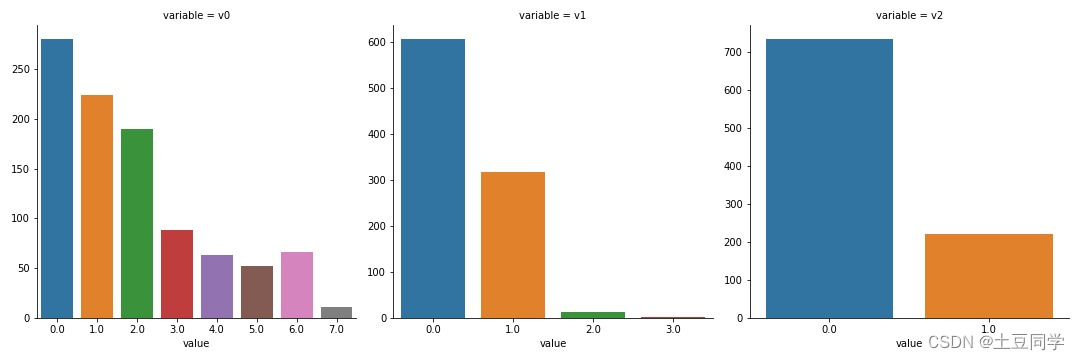
但是多个

count_plot

图只是单纯把几个图集中在一起，不用一个个分别绘制了而已，却无法进一步观察变量之间的关系，所以可以使用上文提到小提琴图进行多变量关系的绘制，具体如下：

plt.figure(figsize=(10,6))
sns.violinplot(x="v0", y="v1", hue="v2",data=data)

从图中可以观察

v2=0

和

v2=1

时，

v0

变化时

v1

的分布变化情况，再来做进一步分析。
如果需要小编使用的实验数据，可以私信小编哦！