0. 前言
2022年没有新写什么博客, 主要精力都在搞论文. 今年开始恢复!
本文的目标是详细分析一个经典的基于landmark(文章后面有时也称之为控制点control point)的图像warping(扭曲/变形)算法: Thin Plate Spine (TPS).
TPS被广泛的应用于各类的任务中, 尤其是生物形态中应用的更多: 人脸, 动物脸等等, TPS是cubic spline的2D泛化形态. 值得注意的是, 图像处理中常用的仿射变换(Affine Transformation), 可以理解成TPS的一个特殊的变种.
- 什么是图像扭曲/变形问题?
[3]给定两张图片中一些相互对应的控制点(landmark, 如图绿色连接线所示),将 图片A(参考图像) 进行特定的形变,使得其控制点可以与 图片B(目标模板) 的landmark重合.
TPS是其中较为经典的方法, 其基础假设是:
如果用一个薄钢板的形变来模拟这种2D形变, 在确保landmarks能够尽可能匹配的情况下,怎么样才能使得钢板的弯曲量(deflection)最小。
- 用法示例 TPS算法在我的实践中, 用法是: 根据图像的landmark(下图左黑色三角), 将2D图像按照映射关系(绿色连接线)到的逻辑变形(warping)到目标模板(下图右).

1. 理论
Thin-Plate-Spline, 本文剩余部分均用其简称TPS来替代. TPS其实是一个数学概念
[1]
:
TPS是1D cubic spline的二维模拟, 它是 双调和方程 (Biharmonic Equation)
[2]
的基本解, 其形式如下:
U
(
r
)
=
r
2
ln
(
r
)
U(r) = r^2 \ln(r)
U(r)=r2ln(r)
1.1
U
(
r
)
U(r)
U(r)形式的由来
那么为什么形式是这样的呢? Bookstein
[10]
在1989年发表的论文 “Principle Warps: Thin-Plate Splines and the Decomposition of Deformation” 中以双调和函数(Biharmonic Equation)的基础解进行展开:
首先,
r
r
r表示的是
x
2
+
y
2
\sqrt{x^2+y^2}
x2+y2(笛卡尔坐标系), 在论文中, Bookstein用的是
U
(
r
)
=
−
r
2
ln
(
r
)
U(r) = -r^2 \ln(r)
U(r)=−r2ln(r), 其目的只是为了可视化方便: **In this pose, it appears to be a slightly dented but otherwise convex surface viewed from above**(即为了看起来中心X点附近的区域是一种 *凹陷(dented)* 的感觉).
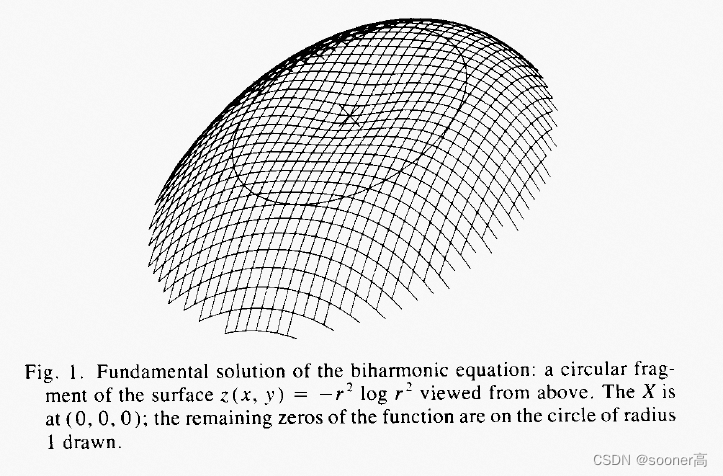
这个函数天然的满足如下方程:
Δ
2
U
=
(
∂
2
∂
x
2
+
∂
2
∂
y
2
)
2
U
∝
δ
(
0
,
0
)
\Delta^2U = (\frac{\partial ^{2}}{\partial x^{2}} + \frac{\partial ^{2}}{\partial y^{2}})^2 U \propto \delta_{(0,0)}
Δ2U=(∂x2∂2+∂y2∂2)2U∝δ(0,0)
公式的左侧和(0,0)的泛函
δ
(
0
,
0
)
\delta_{(0,0)}
δ(0,0)等价(泛函介绍如下),
δ
(
0
,
0
)
\delta_{(0,0)}
δ(0,0)是在除了(0,0)处不等于0外, 任何其它位置都为0的泛函, 其积分为1(我猜, 狄拉克δ函数应该可以理解成这个泛函的一个形态).
所以, 由于双调和函数(Biharmonic Equation)的形式就是
Δ
2
U
=
0
\Delta^2U=0
Δ2U=0, 那么显然,
U
(
r
)
=
(
±
)
r
2
ln
(
r
)
U(r) = (\pm) r^2 \ln(r)
U(r)=(±)r2ln(r)都满足这个条件, 所以它被成为双调和函数的**基础解(fundamental solution)**.
泛函简单来说, 就是定义域为函数集,而值域为实数或者复数的映射, 从知乎
[11]处借鉴来一个泛函的例子:2D平面的两点之间直线距离最短.
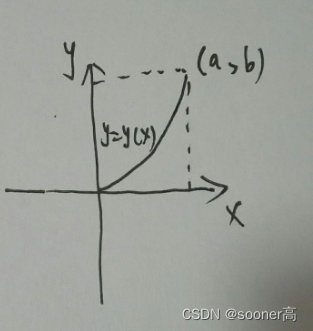
如图所示二维平面空间,从坐标原点(0,0)到点(a,b)的连接曲线是y = y ( x ) y = y(x) y=y(x), 而连接曲线的微元 Δ \Delta Δ或者 d s = 1 + ( d y d x ) 2 d x ds = \sqrt{1+(\frac{dy}{dx})^2dx} ds=1+(dxdy)2dx, 对总的长度, 即为 d s ds ds在 [ 0 , a ] [0, a] [0,a]上的积分: s = ∫ 0 a ( 1 + y ′ 2 ) 1 / 2 d x s = \int_{0}^{a}(1+y^{'2})^{1/2}dx s=∫0a(1+y′2)1/2dx 这里, s s s是**标量(scalar)**, y ′ ( x ) y^{'}(x) y′(x)就是**泛函(functional)**, 通常也记作 s ( y ′ ) s(y^{'}) s(y′). 那么上面的问题就转变成: 找出一条曲线 y ( x ) y(x) y(x),使得泛函 s ( y ′ ) s(y^{'}) s(y′)最小.
好的,
U
U
U的来源和定义清楚了, 那么我们的目标是:
给定一组样本点,以每个样本点为中心的薄板样条(TPS)的加权组合给出了精确地通过这些点的插值函数,同时使所谓的**弯曲能量(bending energy)**最小化.
那么, 什么是所谓的弯曲能量呢?
1.2 弯曲能量: Bending Energy
根据
[1]
, 弯曲能量在这里定义为二阶导数的平方对实数域
R
2
R^2
R2(在我看来, 这里的
R
2
R^2
R2可以**直接理解成2D image的Height and Width, 即高度和宽度**)的积分:
I
[
f
(
x
,
y
)
]
=
∬
(
f
x
x
2
+
2
f
x
y
2
+
f
y
y
2
)
d
x
d
y
I[f(x, y)] = \iint (f_{xx}^2 + 2f_{xy}^2+ f_{yy}^2)dxdy
I[f(x,y)]=∬(fxx2+2fxy2+fyy2)dxdy
优化的目标是要让
I
[
f
(
x
,
y
)
]
I[f(x, y)]
I[f(x,y)]最小化.
好了, 弯曲能量的数学定义到此结束, 很自然的,我们会如下的疑问:
f ( x , y ) f(x, y) f(x,y)是如何定义的?- 对图像这样的2D平面, 其样条的加权组合后的弯曲的方向应该是什么样的, 才能使得弯曲能量最小?
首先我们先分析下弯曲的方向的问题, 并在1.4中进行
f
(
x
,
y
)
f(x, y)
f(x,y)定义的介绍.
1.3 弯曲的方向
首先, 回顾一下TPS的命名, TPS起源于一个物理的类比: the bending of a thin sheet of metal (薄金属片的弯曲).
在物理学上来讲, 弯曲的方向(deflection)是
z
z
z轴, 即垂直于2D图像平面的轴.
为了将这个idea应用于坐标转换的实际问题当中, 我们将TPS理解成是将平板进行拉升 or 降低, 再将拉升/降低后的平面投影到2D图像平面, 即得到根据参考图像和目标模板的landmark对应关系进行warping(形变)后的图像结果.
如下所示, 将平面上设置4个控制点, 其中最后一个不是边缘角点, 在做拉扯的时候, 平面就自然产生了一种局部被拉高或者降低的效果.
显然, 这种warping在一定程度上也是一种坐标转换(coordinate transformation), 如下图所示, 给定参考landmark红色
X
X
X和目标点蓝色
⚪
⚪
⚪. TPS warping将会将这些
X
X
X完美的移动到
⚪
⚪
⚪上.
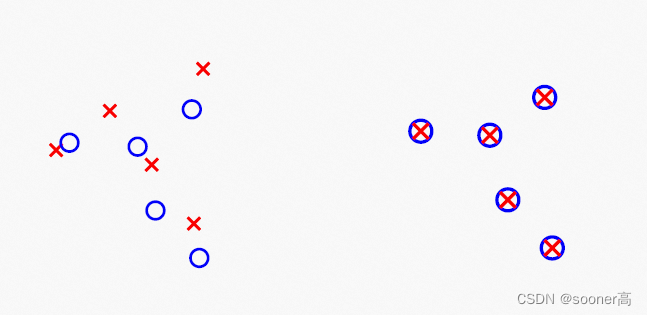
问题来了, 那么这个
X
→
⚪
X \rightarrow ⚪
X→⚪移动的方案是如何实现的呢?
1.4 如何实现2D plane的coordinate transformation (a.k.a warping)?
如下图
[7]
, 2D plane上的坐标变换其实就是2个方向的变化:
X
\mathbf{X}
X 和
Y
\mathbf{Y}
Y方向. 来实现这2个方向的变化, TPS的做法是:
**用2个样条函数分别考虑
X
\mathbf{X}
X和
Y
\mathbf{Y}
Y方向上的位移(displacement)**.
TPS actually use two splines,
one for the displacement in the X direction
and one for the displacement in the Y direction
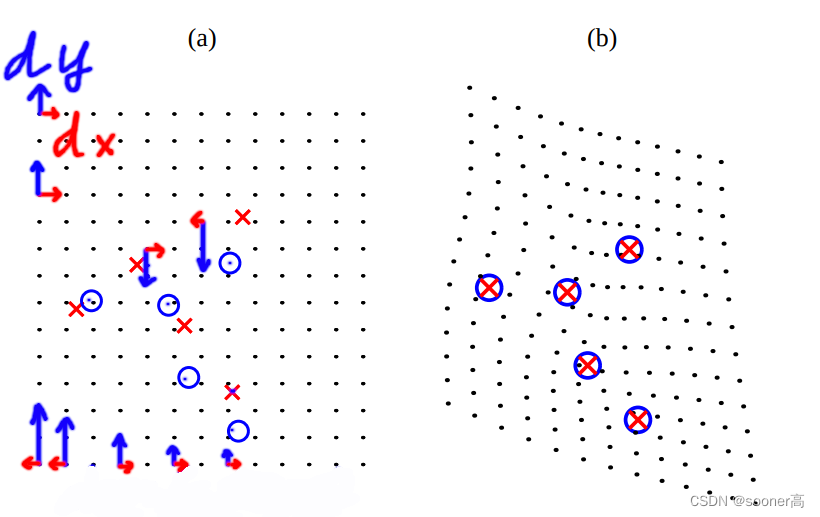
这2个样条函数的定义如下
[7]
(
N
N
N指的是对应的landmark数量, 如上图所示,
N
=
5
N=5
N=5):
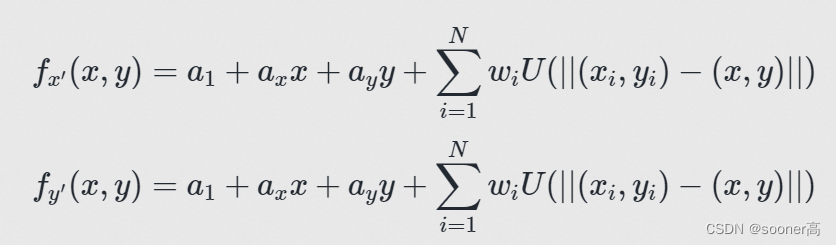
注意, 每个方向(
X
,
Y
\mathbf{X}, \mathbf{Y}
X,Y)的位移(
Δ
X
,
Δ
Y
\mathbf{\Delta X}, \mathbf{\Delta Y}
ΔX,ΔY)可以被视为
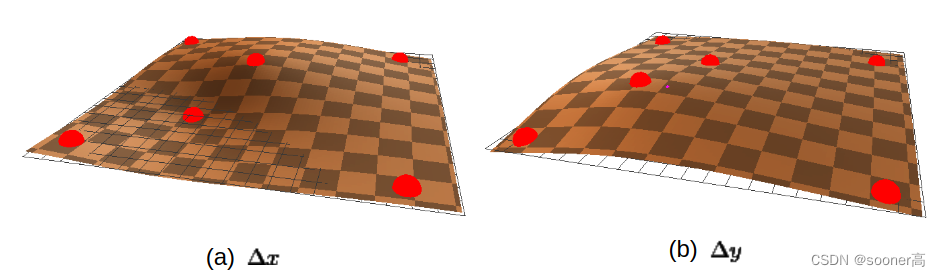
N
N
N个点**高度图(height map)**, 因此样条的就像在3D空间拟合 **散点(scatter point)** 一样, 如下图所示
[7]
.
在样条函数的定义公式中,
- 前3个系数 a 1 , a x , a y a_1, a_x, a_y a1,ax,ay表示线性空间的部分(line part), 用于在线性空间拟合 X X X ( x i , y i x_i, y_i xi,yi)和 ⚪ ⚪ ⚪ ( x i ′ , y i ′ x_i^{'}, y_i^{'} xi′,yi′).
- 紧接着的系数 w i , i ∈ [ 1 , N ] w_i, i \in [1, N] wi,i∈[1,N]表示每个控制点 i i i的kernel weight, 它用于乘以控制点 X X X ( x i , y i x_i, y_i xi,yi)和其最终的 x , y x, y x,y之间的位移(displacement).
- 最后的一项是 U ( ∣ ∣ ( x i , y i ) − ( x , y ) ∣ ∣ ) U(|| (x_i, y_i) - (x, y) ||) U(∣∣(xi,yi)−(x,y)∣∣), 即控制点 X X X ( x i , y i x_i, y_i xi,yi)和其最终的 x , y x, y x,y之间的位移. 需要注意的是, U ( ∣ ∣ ( x i , y i ) − ( x , y ) ∣ ∣ ) U(|| (x_i, y_i) - (x, y) ||) U(∣∣(xi,yi)−(x,y)∣∣)用的是L2范数
[8]. 这里 U U U定义如下: U ( r ) = r 2 ln ( r ) U(r) = r^2 \ln(r) U(r)=r2ln(r) 这里我们需要revisit一下TPS的RBF函数(radial basis function) : U ( r ) = r 2 ln ( r ) U(r) = r^2 \ln(r) U(r)=r2ln(r) , 根据[9]所述, 像RBF这种Gaussian Kernel, 是一种用于衡量相似性的方法(Similarity measurement).
1.5 具体计算方案
对于每个方向(
X
,
Y
\mathbf{X}, \mathbf{Y}
X,Y)的样条函数的系数
a
1
,
a
x
,
a
y
,
w
i
a_1, a_x, a_y, w_i
a1,ax,ay,wi, 可以通过求解如下linear system来获得:
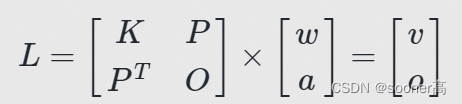
其中,
K
i
j
=
U
(
∣
∣
(
x
i
,
y
i
)
−
(
x
j
,
y
j
)
∣
∣
)
K_{ij} = U(|| (x_i, y_i) - (x_j, y_j) ||)
Kij=U(∣∣(xi,yi)−(xj,yj)∣∣),
P
P
P的第
i
i
i行是齐次表示
(
1
,
x
i
,
y
i
)
(1, x_i, y_i)
(1,xi,yi),
O
O
O是3x3的全0矩阵,
o
o
o是3x1的全0列向量,
w
w
w和
v
v
v是
w
i
w_i
wi和
v
i
v_i
vi组成的列向量.
a
a
a是由
[
a
1
,
a
x
,
a
y
]
[a_1, a_x, a_y]
[a1,ax,ay]组成的列向量.
具体地, 左侧的大矩阵形式如下
[9-10]
:
以N=3(控制点数量为3)为例,
X
\mathbf{X}
X方向的样条函数的线性矩阵表达为:
[
U
11
U
21
U
31
1
x
1
y
1
U
12
U
22
U
32
1
x
2
y
2
U
13
U
23
U
33
1
x
3
y
3
1
1
1
0
0
0
x
1
x
2
x
3
0
0
0
y
1
y
2
y
3
0
0
0
]
×
[
w
1
w
2
w
3
a
1
a
x
a
y
]
=
[
x
1
′
x
2
′
x
3
′
0
0
0
]
\begin{bmatrix} U_{11} & U_{21} & U_{31} & 1 & x_1 & y_1\\ U_{12} & U_{22} & U_{32} & 1 & x_2 & y_2\\ U_{13} & U_{23} & U_{33} & 1 & x_3 & y_3 \\ 1 & 1 & 1 & 0 & 0& 0 \\ x_1 & x_2 & x_3 & 0 & 0& 0 \\ y_1 & y_2 & y_3 & 0 & 0& 0 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ a_1 \\ a_x \\ a_y \end{bmatrix} = \begin{bmatrix} x_1^{'} \\ x_2^{'} \\ x_3^{'} \\ 0 \\ 0 \\ 0 \end{bmatrix}
U11U12U131x1y1U21U22U231x2y2U31U32U331x3y3111000x1x2x3000y1y2y3000×w1w2w3a1axay=x1′x2′x3′000
同样地,
Y
\mathbf{Y}
Y的样条函数的线性矩阵表达为:
[
U
11
U
21
U
31
1
x
1
y
1
U
12
U
22
U
32
1
x
2
y
2
U
13
U
23
U
33
1
x
3
y
3
1
1
1
0
0
0
x
1
x
2
x
3
0
0
0
y
1
y
2
y
3
0
0
0
]
×
[
w
1
w
2
w
3
a
1
a
x
a
y
]
=
[
y
1
′
y
2
′
y
3
′
0
0
0
]
\begin{bmatrix} U_{11} & U_{21} & U_{31} & 1 & x_1 & y_1\\ U_{12} & U_{22} & U_{32} & 1 & x_2 & y_2\\ U_{13} & U_{23} & U_{33} & 1 & x_3 & y_3 \\ 1 & 1 & 1 & 0 & 0& 0 \\ x_1 & x_2 & x_3 & 0 & 0& 0 \\ y_1 & y_2 & y_3 & 0 & 0& 0 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ a_1 \\ a_x \\ a_y \end{bmatrix} = \begin{bmatrix} y_1^{'} \\ y_2^{'} \\ y_3^{'} \\ 0 \\ 0 \\ 0 \end{bmatrix}
U11U12U131x1y1U21U22U231x2y2U31U32U331x3y3111000x1x2x3000y1y2y3000×w1w2w3a1axay=y1′y2′y3′000
显然可见, N+3个函数来求解N+3个未知量, 能得到相应的
[
w
a
]
\begin{bmatrix} w \\ a \end{bmatrix}
[wa].
2. 代码实现
我使用的TPS是cheind/py-thin-plate-spline项目
[6]
, 这里会对代码进行详细拆解, 以达到理解公式和实现的对应关系.
2.1 核心计算逻辑
核心逻辑在函数
warp_image_cv
中:
tps.tps_theta_from_points
,
tps.tps_grid
和
tps.tps_grid_to_remap
,
最基本的示例代码如下:
defshow_warped(img, warped, c_src, c_dst):
fig, axs = plt.subplots(1,2, figsize=(16,8))
axs[0].axis('off')
axs[1].axis('off')
axs[0].imshow(img[...,::-1], origin='upper')
axs[0].scatter(c_src[:,0]*img.shape[1], c_src[:,1]*img.shape[0], marker='^', color='black')
axs[1].imshow(warped[...,::-1], origin='upper')
axs[1].scatter(c_dst[:,0]*warped.shape[1], c_dst[:,1]*warped.shape[0], marker='^', color='black')
plt.show()defwarp_image_cv(img, c_src, c_dst, dshape=None):
dshape = dshape or img.shape
theta = tps.tps_theta_from_points(c_src, c_dst, reduced=True)
grid = tps.tps_grid(theta, c_dst, dshape)
mapx, mapy = tps.tps_grid_to_remap(grid, img.shape)return cv2.remap(img, mapx, mapy, cv2.INTER_CUBIC)
img = cv2.imread('test.jpg')
c_src = np.array([[0.44,0.18],[0.55,0.18],[0.33,0.23],[0.66,0.23],[0.32,0.79],[0.67,0.80],])
c_dst = np.array([[0.693,0.466],[0.808,0.466],[0.572,0.524],[0.923,0.524],[0.545,0.965],[0.954,0.966],])
warped_front = warp_image_cv(img, c_src, c_dst, dshape=(512,512))
show_warped(img, warped1, c_src_front, c_dst_front)

此开源代码有2个版本: numpy和torch. 这里我的分析以numpy版本进行, 以便没有GPU用的朋友进行hands-on的测试.
核心类TPS
classTPS:@staticmethoddeffit(c, lambd=0., reduced=False): n = c.shape[0] U = TPS.u(TPS.d(c, c)) K = U + np.eye(n, dtype=np.float32)*lambd P = np.ones((n,3), dtype=np.float32) P[:,1:]= c[:,:2] v = np.zeros(n+3, dtype=np.float32) v[:n]= c[:,-1] A = np.zeros((n+3, n+3), dtype=np.float32) A[:n,:n]= K A[:n,-3:]= P A[-3:,:n]= P.T theta = np.linalg.solve(A, v)# p has structure w,areturn theta[1:]if reduced else thete ...@staticmethoddefz(x, c, theta): x = np.atleast_2d(x) U = TPS.u(TPS.d(x, c)) w, a = theta[:-3], theta[-3:] reduced = theta.shape[0]== c.shape[0]+2if reduced: w = np.concatenate((-np.sum(w, keepdims=True), w)) b = np.dot(U, w)return a[0]+ a[1]*x[:,0]+ a[2]*x[:,1]+ b
2.2
tps.tps_theta_from_points
此函数的作用是为了求解样条函数的
[
w
a
]
\begin{bmatrix} w \\ a \end{bmatrix}
[wa].
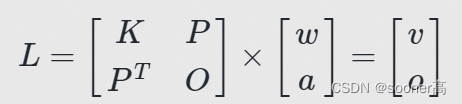
deftps_theta_from_points(c_src, c_dst, reduced=False):
delta = c_src - c_dst
cx = np.column_stack((c_dst, delta[:,0]))
cy = np.column_stack((c_dst, delta[:,1]))
theta_dx = TPS.fit(cx, reduced=reduced)
theta_dy = TPS.fit(cy, reduced=reduced)return np.stack((theta_dx, theta_dy),-1)
- delta 是 在参考图的控制点和目标模板的控制点之间的插值 Δ x i , Δ y i \Delta x_i, \Delta y_i Δxi,Δyi
- cx和cy是在
c_dst的基础上, 分别加了 Δ x i \Delta x_i Δxi和 Δ y i \Delta y_i Δyi的列向量 - theta_dx和theta_dy的reduce参数默认为False/True时. 其结果是1D向量, 长度为9/8 . 其计算过程需要看TPS核心类的
fit函数.
①
TPS.d(cx, cx, reduced=True)
or
TPS.d(cy, cy, reduced=True)
计算L2
@staticmethoddefd(a, b):# a[:, None, :2] 是把a变成[N, 1, 2]的tensor/ndarray# a[None, :, :2] 是把a变成[1, N, 2]的tensor/ndarrayreturn np.sqrt(np.square(a[:,None,:2]- b[None,:,:2]).sum(-1))
其作用是计算样条中的
∣
∣
(
x
i
,
y
i
)
−
(
x
,
y
)
∣
∣
|| (x_i, y_i) - (x, y) ||
∣∣(xi,yi)−(x,y)∣∣ (**L2**), 得出的结果是shape为
N
,
N
N, N
N,N的中间结果.
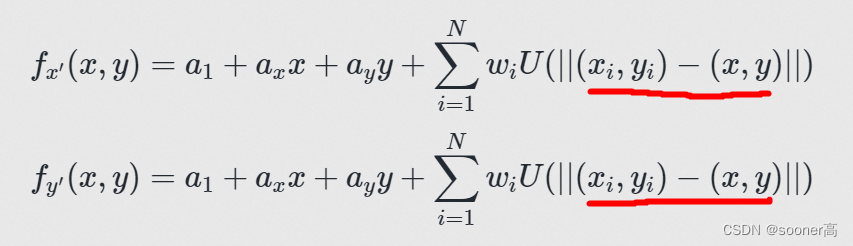
②
TPS.u(...)
**计算
U
(
.
.
.
)
U(...)
U(...)**
和公式完全一样:
U
(
r
)
=
r
2
ln
(
r
)
U(r) = r^2 \ln(r)
U(r)=r2ln(r), 为了防止
r
r
r太小, 加了个epsilon系数
1
e
−
6
1e^{-6}
1e−6. 这一步得到
K
K
K, shape仍然是
N
,
N
N, N
N,N, 和①一样.
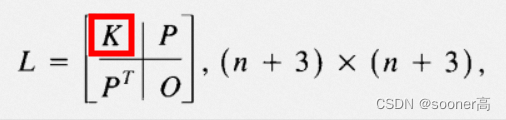
defu(r):return r**2* np.log(r +1e-6)
③ 根据
cx
和
cy
, 简单拼接即可生成
P
.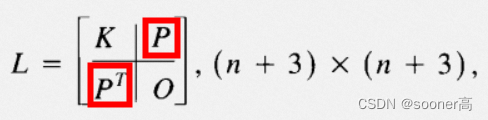
P = np.ones((n,3), dtype=np.float32)
P[:,1:]= c[:,:2]# c就是cx or cy.
④ 根据
Δ
x
i
\Delta x_i
Δxi (
cx
得最后一列向量,
cy
同理), 得到
v
v
v

# c = cx or cy
v = np.zeros(n+3, dtype=np.float32)
v[:n]= c[:,-1]
⑤ 组装矩阵
A
, 即
[10]
论文中的
L
L
L矩阵.
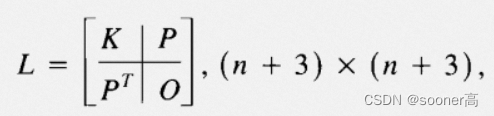
A = np.zeros((n+3, n+3), dtype=np.float32)
A[:n,:n]= K
A[:n,-3:]= P
A[-3:,:n]= P.T
⑥ 现在
L
L
L和
Y
Y
Y已知,
Y
=
[
v
o
]
Y = \begin{bmatrix}v \\ o \end{bmatrix}
Y=[vo], 那么
W
W
W和
a
1
,
a
x
,
a
y
a_1, a_x, a_y
a1,ax,ay的向量可以直接线性求解
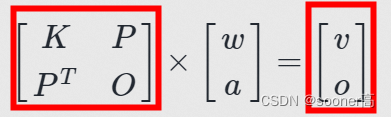
[
w
a
]
\begin{bmatrix}w \\ a \end{bmatrix}
[wa] =
L
−
1
L^{-1}
L−1
Y
Y
Y
classTPS:@staticmethoddeffit(c, lambd=0., reduced=False):# 1. TPS.d
U = TPS.u(TPS.d(c, c))
K = U + np.eye(n, dtype=np.float32)*lambd
P = np.ones((n,3), dtype=np.float32)
P[:,1:]= c[:,:2]
v = np.zeros(n+3, dtype=np.float32)
v[:n]= c[:,-1]
A = np.zeros((n+3, n+3), dtype=np.float32)
A[:n,:n]= K
A[:n,-3:]= P
A[-3:,:n]= P.T
theta = np.linalg.solve(A, v)# p has structure w,areturn theta[1:]if reduced else theta
@staticmethoddefd(a, b):return np.sqrt(np.square(a[:,None,:2]- b[None,:,:2]).sum(-1))@staticmethoddefu(r):return r**2* np.log(r +1e-6)
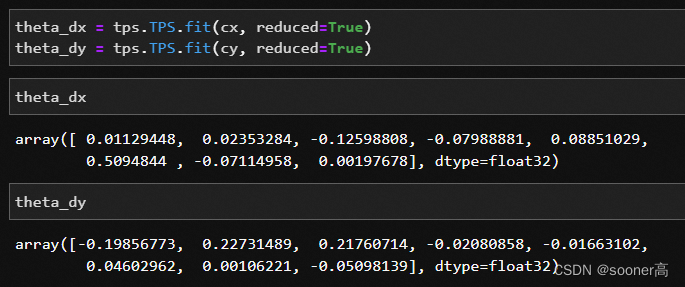
即函数返回的
theta
就是
[
w
a
]
\begin{bmatrix}w \\ a \end{bmatrix}
[wa]. 由于我们是2个方向(X, Y)都要这个
theta
, 因此
theta = tps.tps_theta_from_points(c_src, c_dst)
返回的theta是
(
N
+
3
,
2
)
(N+3, 2)
(N+3,2)的形式.
2.3
tps.tps_grid
此函数是为了求解image plane在x和y方向上的偏移量(offset).
defwarp_image_cv(img, c_src, c_dst, dshape=None):
dshape = dshape or img.shape
# 2.2
theta = tps.tps_theta_from_points(c_src, c_dst, reduced=True)# 2.3
grid = tps.tps_grid(theta, c_dst, dshape)# 2.4
mapx, mapy = tps.tps_grid_to_remap(grid, img.shape)return cv2.remap(img, mapx, mapy, cv2.INTER_CUBIC)
由核心代码部分可以看出, 当求出
theta
, 也就是
[
w
a
]
\begin{bmatrix}w \\ a \end{bmatrix}
[wa]. 我们下面用
tps_grid
函数进行网格的warping操作.
函数如下:
deftps_grid(theta, c_dst, dshape):# 1) uniform_grid(...)
ugrid = uniform_grid(dshape)
reduced = c_dst.shape[0]+2== theta.shape[0]# 2) 求dx和dy.
dx = TPS.z(ugrid.reshape((-1,2)), c_dst, theta[:,0]).reshape(dshape[:2])
dy = TPS.z(ugrid.reshape((-1,2)), c_dst, theta[:,1]).reshape(dshape[:2])
dgrid = np.stack((dx, dy),-1)
grid = dgrid + ugrid
return grid # H'xW'x2 grid[i,j] in range [0..1]
其输入是3个参数:
- theta
reduced=True(N+2, 2) orreduced=False(N+3, 2) - c_dst (N, 2), 是目标模板上的control points or landmarks.
c_dst = np.array([[0.693,0.466],[0.808,0.466],[0.572,0.524],[0.923,0.524],[0.545,0.965],[0.954,0.966],])
- dshape (H, W, 3), 是给定参考图像的分辨率.
输出是1个:
- grid (H, W, 2). 其可视化效果见
2.3.1.
2.3.1
uniform_grid
tps.tps_grid
函数的第一步是ugrid = uniform_grid(dshape), 此函数的定义如下, 作用是创建1个
(
H
,
W
,
2
)
(H, W, 2)
(H,W,2)的grid, 里面的值都是0到1的线性插值
np.linspace(0, 1, W(H))
.
defuniform_grid(shape):'''Uniform grid coordinates.
'''
H,W = shape[:2]
c = np.empty((H, W,2))
c[...,0]= np.linspace(0,1, W, dtype=np.float32)
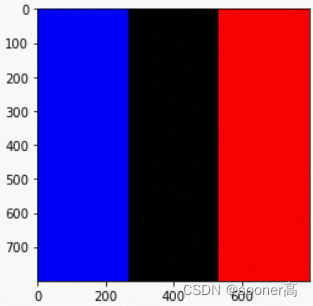
c[...,1]= np.expand_dims(np.linspace(0,1, H, dtype=np.float32),-1)return c
返回的
ugrid
就是一个
(
H
,
W
,
2
)
(H, W, 2)
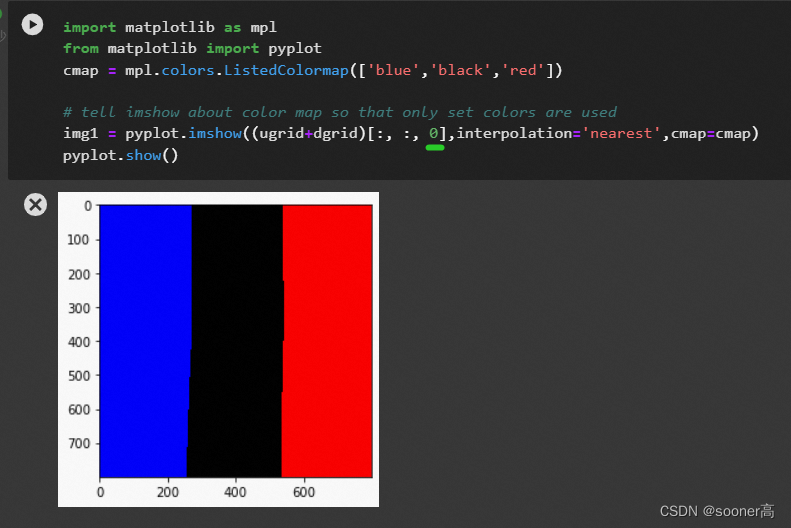
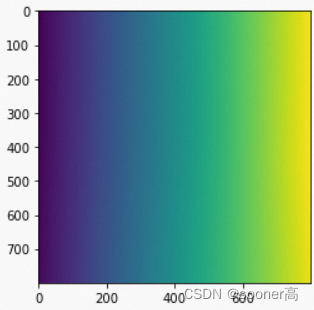
(H,W,2)的grid, 其X, Y方向值的大小按方向线性展开, 如下图所示.
X方向
Y方向
2.3.2
TPS.z
求解得到
dx
和
dy
# 2) 求dx和dy.
dx = TPS.z(ugrid.reshape((-1,2)), c_dst, theta[:,0]).reshape(dshape[:2])# [H, W]
dy = TPS.z(ugrid.reshape((-1,2)), c_dst, theta[:,1]).reshape(dshape[:2])# [H, W]
dgrid = np.stack((dx, dy),-1)# [H, W, 2]
grid = dgrid + ugrid
由下面的
TPS.z
定义容易看出, 这个函数就是求解X和Y方向的样条函数:
f
(
x
/
y
)
′
(
x
,
y
)
=
a
1
+
a
x
x
+
a
y
y
+
∑
i
=
1
N
w
i
U
(
∣
∣
(
x
i
,
y
i
)
−
(
x
,
y
)
∣
∣
)
f_{(x/y)^{'}}(x, y) = a_1 + a_x x + a_y y + \sum_{i=1}^{N} w_i U(|| (x_i, y_i) - (x, y) ||)
f(x/y)′(x,y)=a1+axx+ayy+i=1∑NwiU(∣∣(xi,yi)−(x,y)∣∣)
可能让人有困惑的点是说, **为什么在
2.2
的时候,
TPS.d()
的传参是一样的(
cx(cy)
), 而这里的x是shape为
(H*W), 2
, 而
c
仍旧是
c_dst (N,2)
**, 我的理解是说, 由于
2.3
这一步的目标是为了真正的让image plane按照控制点的位置进行移动(最小化弯曲能量), 所以通过
ugrid
均匀对平面采样的点进行offset计算(
dx
和
dy
), 使其得到满足推导条件下的offset解析解
dgrid
.
classTPS:...@staticmethoddefz(x, c, theta):
x = np.atleast_2d(x)
U = TPS.u(TPS.d(x, c))# [H*W, N] 本例中H=W=800, N=6
w, a = theta[:-3], theta[-3:]
reduced = theta.shape[0]== c.shape[0]+2if reduced:
w = np.concatenate((-np.sum(w, keepdims=True), w))
b = np.dot(U, w)return a[0]+ a[1]*x[:,0]+ a[2]*x[:,1]+ b
所以对
ugrid
dgrid, 即得到整个图像平面按照样条函数计算出来的
d x , d y dx, dydx,dy(offset)加到均匀的
ugrid
的结果: 显然可以看出, 这个结果相比
2.3.1
的
ugrid
, 在
X
,
Y
\mathbf{X}, \mathbf{Y}
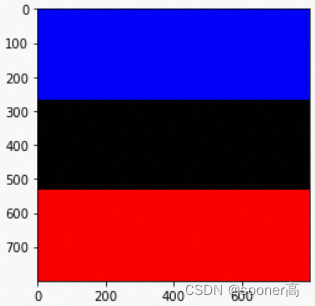
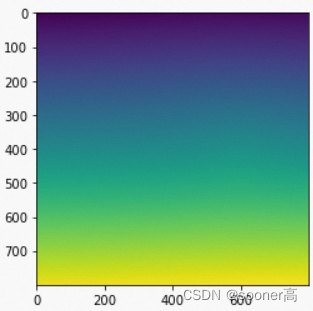
X,Y方向有了相应的变化.
X方向
Y方向
到这里,
2.3
这步返回的其实就是一个在
X
,
Y
\mathbf{X}, \mathbf{Y}
X,Y方向相应扭曲的**grid(格子)**
(
H
,
W
,
2
)
(H, W, 2)
(H,W,2), 其可视化结果如上, 值的范围都在 **-1到1** 之间.
2.4
tps.tps_grid_to_remap
这一步很简单了, 就是把
2.3
计算得到的**grid(格子)**按
X
,
Y
\mathbf{X}, \mathbf{Y}
X,Y方向分别乘以对应的
W
W
W和
H
H
H. 然后送去
cv2.remap
函数进行图像的扭曲操作.
defwarp_image_cv(img, c_src, c_dst, dshape=None):
dshape = dshape or img.shape
# 2.2
theta = tps.tps_theta_from_points(c_src, c_dst, reduced=True)# 2.3
grid = tps.tps_grid(theta, c_dst, dshape)# 2.4
mapx, mapy = tps.tps_grid_to_remap(grid, img.shape)return cv2.remap(img, mapx, mapy, cv2.INTER_CUBIC)
2.4.1
tps_grid_to_remap
简单的把grid乘以宽和高
deftps_grid_to_remap(grid, sshape):'''Convert a dense grid to OpenCV's remap compatible maps.
Returns
-------
mapx : HxW array
mapy : HxW array
'''
mx =(grid[:,:,0]* sshape[1]).astype(np.float32)
my =(grid[:,:,1]* sshape[0]).astype(np.float32)return mx, my
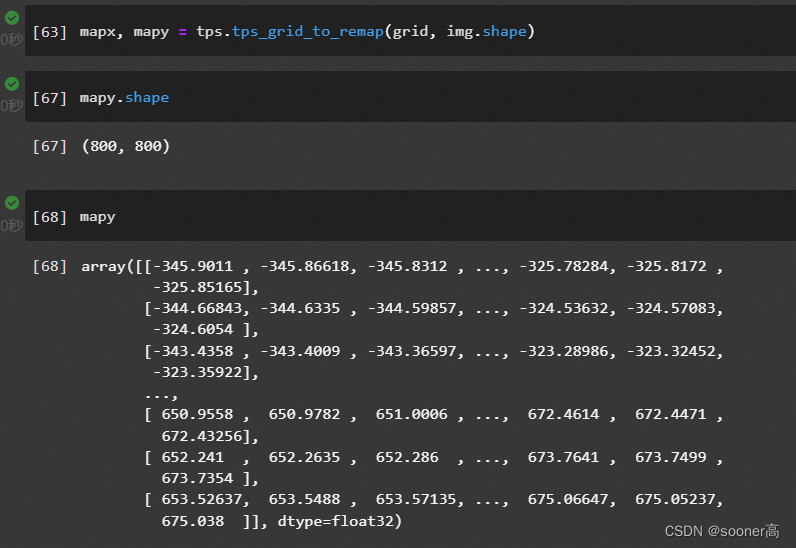
2.4.2
cv2.remap(img, mapx, mapy, cv2.INTER_CUBIC)
得到warp后的结果.
cv2.remap
是允许用户自己定义映射关系的函数, 不同于通过变换矩阵进行的仿射变换和透视变换, 更加的灵活,
TPS
就是使用的这种映射. 具体示例参考
[12]
.
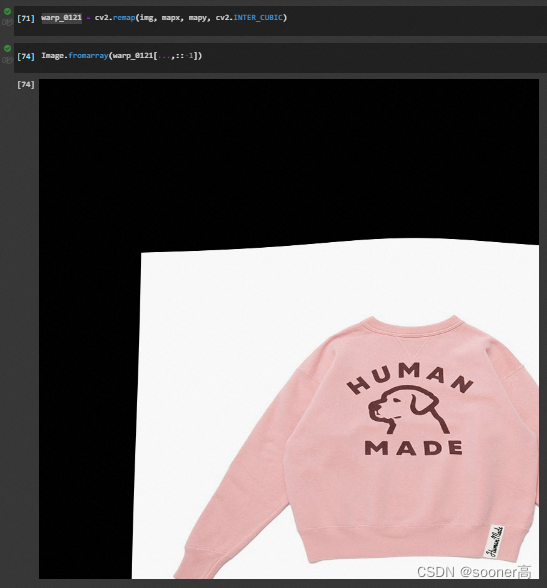
需要注意的是, 这个结果之所以和前言中的不一样, 是因为在前言里, 我们用了mask来做遮罩.
总结
到这里,
TPS
的分析就告一段落了, 这种算法是瘦脸, 纹理映射等任务中最常见的, 也是很灵活的warping算法, 目前还仍然在广泛使用, 如果文章哪里写的有谬误或者问题, 欢迎大家在下面指出,
感谢 ^ . ^
参考文献
- Thin Plate Spline: MathWorld
- Biharmonic Equation: MathWorld
- c0ldHEart: Thin Plate Spline TPS薄板样条变换基础理解
- MIT: WarpMorph
- Approximation Methods for Thin Plate Spline Mappings and Principal Warps
- cheind/py-thin-plate-spline
- Thin-Plate-Splines-Warping
- Wikipedia: Thin plate spline
- Deep Shallownet: Radial Basis Function Kernel - Gaussian Kernel
- Bookstein: Principle Warps: Thin Plate Splines and the Decomposition of Deformations
- 知乎:「泛函」究竟是什么意思?
- 【opencv】5.5 几何变换-- 重映射 cv2.remap()
版权归原作者 sooner高 所有, 如有侵权,请联系我们删除。