摘要
本文通过结合P-M微分模型与中值滤波进行去噪设计,提出了LMFPM的去噪模型。该模型对P-M法中的扩散函数中的图像梯度模进行处理,为其增加中值滤波的线性影响,以实现对噪声和边界的区分处理,解决了P-M法中对小尺度噪声处理效果不好的问题。对提出的模型利用有限差分法进行数值计算,然后用实验对比均值滤波、中值滤波和P-M法分别对Lena图像和Cameraman图像进行去噪处理,使用峰值信噪比(PSNR)、信噪比(SNR)和平均结构相似度(MSSIM)来作为客观评价指标
研究结果表明本文改进算法(LMFPM)优于均值滤波、中值滤波、P-M算法,可以有效地去除混合噪声,在提高信噪比和平均结构相似度的同时保留了图像的细节信息,可以更好地满足图像去噪的要求。
1.1 P-M改进型微分方程
与热扩散模型相比较,各向异性扩散模型实际上是一个非线性的偏微分方程,由图像的梯度来决定扩散速度,能够同时兼顾噪声消除和特征保持2个方面.目前,以Perona.Malik(PM)模型为代表的各向异性平滑方法己在边缘检测、图像增强、图像分割以及目标识别等领域得到了广泛的应用。但P-M模型在对小尺度噪声点处理效果并不理想,因此本文中给出结合中值滤波的改进型P-M模型。
1.1.1 P-M微分方程
P-M模型是一种经典的非线性图像扩散模型,该模型能根据设定的阈值对图像光滑区域进行扩散,并能自适应地保持图像边缘[8]。针对各向同性扩散在去噪的同时会模糊图像的边缘,1990年,Perona和Malik在传统的热扩散方程的基础上,提出了基于非线性偏微分方程的新模型即各向异性扩散模型。
图像在尺度空间中被划分为不同尺度的区域,P-M算法的思想就是在尺度区域内进行平滑,而在尺度区域与尺度区域之间即边缘或边界减少多余的平滑甚至不平滑。从某种程度上来说,P-M算法对图像的边缘进行了“增强”。在P-M算法中,边缘采用常用的梯度微分算子来识别,这可以理解为模型将边缘检测和噪声去除很好地统一到了变分方法的偏微分方程中[9]。从数学意义上来分析,P-M模型实质上是改进的热传导(热扩散)偏微分方程: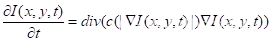
其中,I(x,y,t)是原始图像,(x,y)是扩散过程的空间信息。 表示步长,同时也是扩散过程的时间信息,div和 分别表示散度算子和梯度算子,c(·)是扩散系数。如果c(·)是一个常数,那么扩散就是各向同性的,它的效果等同于线性低通滤渡。在PM模型中,c(·)是关于梯度的函数,即在梯度低的区域平滑效果很强,而在接近边缘梯度较高的区域P-M模型尽可能地减少平滑甚至不平滑,这样就实现了保边缘平滑。Perona和Malik在研究中还提出4-邻域离散形式的各向异性的扩散方程: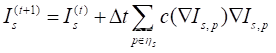
这里,c(·)是关于梯度的单调递减函数, 代表着中心像素s相邻的区域。Perona和Malik提出了两种具有启发性的扩散系数函数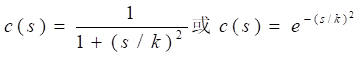
其中K 是门限阈值,用于判断图像的特征。扩散系数式是一个关于梯度大小的单调递减函数。当梯度较小时,意味着对应的中心像素在尺度区域内,这时扩散方程如同低通滤波一样进行平滑;当梯度较大的时候,意味着对应的中心像素是边缘或者在边缘附近,这时扩散方程扩散的行为变得很不明显,从而保持了图像的边缘信息。
1.1.2 LMFPM去噪模型
P-M 模型在一定程度上去除了图像噪声,提高了图像的清晰度,但常常不能够有效地消除小尺度区域的噪声和梯度很大的突变。而中值滤波由于可对长拖尾概率分布的噪声起到良好的平滑效果且可对图像中的某些细节起到保护作用,因而在图像降噪处理中得到了比较广泛的应用[10]。
为此,本文提出了一种改进型P-M模型,即基于中值滤波的各向异性扩散(Linear Median Filter P-M,LMFPM)模型。LMFPM模型的基本思想是对图像梯度模进行处理,为其增加中值滤波的线性影响。用经过中值滤波平滑后的梯度模代替原始图像的扩散函数梯度模,并且为中值滤波器增加线性权重以控制中值滤波的影响,从而控制扩散的过程。中值滤波能去除图像中的强噪声,对椒盐噪声等小尺度区域的噪声图像有较好的去噪效果,同时还去掉了边界上的一些噪点,不必要的细节和噪点信息将不会影响扩散,经过平滑后的梯度模更能准确反映图像边缘的变化。
LMFPM模型是基于P-M模型构建的去噪处理,由于经典的P-M模型的扩散系数的设计使P-M模型的边缘保持效果不理想。该扩散系数对噪声边缘和对图像的边缘区分度较低,因此LMFPM模型对P-M的扩散系数进行处理,将公式改写为: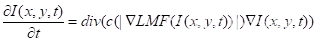
其中
MF(·)是中值滤波,在此采用的是3×3的模板, 是中值滤波所占比例系数。改写后的模型会对扩散系数中的变量进行预处理,先用中值滤波去除小尺度的噪声,再进行计算。由此得到的扩散系数会对噪声和图像边缘有区分的处理,因此得到的图像比经典P-M模型处理出的图像效果更好。
2.2 设计去噪处理
(1). LMFPM处理函数:为获得图片参数信息、转换图片类型等,首先对图像进行预处理和给出初始条件。然后进行多轮迭代,此处的迭代分为外迭代和内迭代,外迭代用于控制迭代LMFPM对图像去噪的处理次数,内迭代用于对单次外迭代的图像内部处理。在每次外迭代中引入中值滤波处理图像,再进行图片内部迭代,对图片内部的每个像素点进行差分并计算采用LMFPM模型处理后的图像,其中的微分计算采用水平方向、竖直方向和两个倾斜方向的这四个方向进行差分近似处理。最后进行边界处理,再进入下一轮的外迭代,符合终止条件后退出循环,得到处理后的图像。
(2). 主程序:先对原图像进行清空变量、类型转换等基础处理,再对图片进行加噪处理,调用中值去噪、均值去噪、P-M法去噪以及LMFPM法去噪进行对比。绘制图像以主观判断去噪效果,并以峰值信噪比(PSNR)、信噪比(SNR)和平均结构相似度(MSSIM)进行客观评价,本文用到的例子中的扩散系数则采用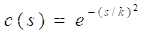
的计算公式。本文例子中的MSSIM则是采用高斯函数sigma=1.5的3×3模板
2.2 灰度图像实验结果分析
灰度图像选取 Lena 图像和 Cameraman 图像,对实验对象同时加入噪声密度为0.01的椒盐噪声与均值为0.01,方差为0.01的高斯噪声这两种的混合噪声,取时间步长Δt = 0.1,用均值滤波、中值滤波、P-M法和LMFPM法进行对比,在 MATLAB R2019a 的环境中进行实验。
2.2.1 Lena图的实验结果分析
在此采用的均值滤波模板为: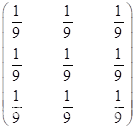
中值滤波模板为3×3的模板,P-M法和LMFPM法的迭代次数、门限阈值分别为20和15,LMFPM的中值滤波比例为0.85。去噪指标中MSSIM模板采用的为高斯函数sigma=1.5的3×3模板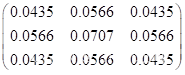
得到的图像结果如下:
去噪评价指标:
从主观上来看,可以明显看出LMFPM的效果最好,与原图像最接近。从去噪评价指标的表格数据来看,也可看出经用LMFPM法处理过的图像在PSNR、MSSIM、SNR这三个方面的指标数据明显高于其他去噪方法,说明本文中提出的LMFPM模型确实有较好的去噪效果
2.2.2 Cameraman图像的实验结果分析
在此与Lena图像相似地采用的均值滤波模板为: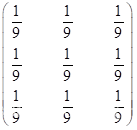
中值滤波模板为3×3的模板,P-M法和LMFPM法的迭代次数、门限阈值分别为10和15,LMFPM的中值滤波比例为0.95。去噪指标中MSSIM模板采用的为高斯函数sigma=1.5的3×3模板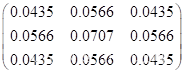
得到的图像结果如下:
去噪评价指标:
同样地,从主观上来看,与Lena图像相似地可以明显看出LMFPM的效果最好,与原图像最接近。从去噪评价指标的表格数据来看,也可看出经用LMFPM法处理过的图像在PSNR、MSSIM、SNR这三个方面的指标数据明显高于其他去噪方法,说明本文中提出的LMFPM模型确实有较好的去噪效果
3. 结束语
本文提出了一种新的图像去噪模型,并选取不同的灰度图像进行 MATLAB 实验。从去噪图像的直观效果和表格中的客观数据来看,用本文LMFPM模型去噪后的图像质量均高于均值滤波、中值滤波和P-M模型。因此,本文模型可以有效去除混合噪声,同时也很好地保留了图像边缘细节信息
代码部分(MATLAB):
PSNR指标
function [ out ] = PSNR( X,Y )
%%
%PSNR(Peak Signal to Noise Ratio)峰值信噪比:
% MSE表示当前图像X和参考图像Y的均方误差(Mean Square Error),H、W分别为图像的高度和宽度;
% PSNR的单位是dB,数值越大表示失真越小。n为每像素的比特数,一般的灰度图像取8,即像素灰阶数为256.
% PSNR是最普遍和使用最为广泛的一种图像客观评价指标,然而它是基于对应像素点间的误差,即基于误差敏感的图像质量评价。
%%
[ m,n ] = size( X );
mse = sum(( double(X(:)) - double(Y(:)) ).^2);
mse = mse/(m*n);
out = 10*log10((255*255)/mse);
end
SNR指标
function isnr = SNR(oriImg, noiImg)
ps = sum((oriImg(:)-mean(oriImg(:))).^2); % signal power
pn = sum((oriImg(:)-noiImg(:)).^2);
isnr = 10*log10(ps/pn);
end
MSSIM指标
function [mssim, ssim_map] = MSSIM(img1, img2, K, window, L)
%%
% MSSIM(Mean Structural Similarity )平均结构相似性
% 在实际应用中,可以利用滑动窗将图像分块,令分块总数为N,考虑到窗口形状对分块的影响,采用加权计算每一窗口的均值、方差以及协方差,
% 权值wij满足∑i∑jwij=1,通常采用高斯核,然后计算对应块的结构相似度SSIM,最后将平均值作为两图像的结构相似性度量,即平均结构相似性MSSIM
%%
C1 = (K(1)*L)^2;
C2 = (K(2)*L)^2;
window = window/sum(sum(window));
img1 = double(img1);
img2 = double(img2);
mu1 = filter2(window, img1, 'valid');
mu2 = filter2(window, img2, 'valid');
mu1_sq = mu1.*mu1;
mu2_sq = mu2.*mu2;
mu1_mu2 = mu1.*mu2;
sigma1_sq = filter2(window, img1.*img1, 'valid') - mu1_sq;
sigma2_sq = filter2(window, img2.*img2, 'valid') - mu2_sq;
sigma12 = filter2(window, img1.*img2, 'valid') - mu1_mu2;
if (C1 > 0 && C2 > 0)
ssim_map = ((2*mu1_mu2 + C1).*(2*sigma12 + C2))./((mu1_sq + mu2_sq + C1).*(sigma1_sq + sigma2_sq + C2));
else
numerator1 = 2*mu1_mu2 + C1;
numerator2 = 2*sigma12 + C2;
denominator1 = mu1_sq + mu2_sq + C1;
denominator2 = sigma1_sq + sigma2_sq + C2;
ssim_map = ones(size(mu1));
index = (denominator1.*denominator2 > 0);
ssim_map(index) = (numerator1(index).*numerator2(index))./(denominator1(index).*denominator2(index));
index = (denominator1 ~= 0) & (denominator2 == 0);
ssim_map(index) = numerator1(index)./denominator1(index);
end
mssim = mean2(ssim_map);
return
P-M法
function diff_im = myec_ns(im, num_iter, delta_t, kappa)
%myec_ns 经典PM模型的4方向扩散
% DIFF_IM = myec_ns(IM, NUM_ITER, DELTA_T, KAPPA, OPTION)
% 该函数执行灰度图像上的各向异性扩散(经典PM模型),被认为是一个二维的网络结构的4个方向的扩散传导。
%
% 参数描述:
% IM - 灰度图 (MxN).
% NUM_ITER - 迭代次数
% DELTA_T - 迭代系数
% KAPPA - 控制传导的梯度模阈值。控制平滑。
% 扩散函数c(x,y,t) = exp(-(gards(mf_diff_im)/kappa).^2)
% 输出描述:
% DIFF_IM - 具有最大尺度空间参数的(扩散)图像。
%
% 使用例子:
% -------------
% s = phantom(512) + randn(512);
% num_iter = 15;
% delta_t = 1/7;%越大越平滑
% kappa = 20;%越大越平滑
% ad = myec_ns(s,num_iter,delta_t,kappa);
% figure, subplot 121, imshow(s,[]), subplot 122, imshow(ad,[]);
% 转换输入图像类型为double.
im = double(im);
[M,N]=size(im);
% PDE(偏微分方程)的初始条件。
diff_im = im;
% 中心像素距离。
dx = 1;
dy = 1;
dd = sqrt(2);
% 各向异性扩散
for t = 1:num_iter %迭代次数
for i=2:M-1
for j=2:N-1 %迭代元素
% 在竖直,水平,左右斜方,这四个方向进行两次差分并在第一次差分时带入扩散函数,即
% (diff(t+1)-diff(t))/dt=
% ((c(j+1)diff(j+1)-c(j+1)diff(j))/dx - (c(j)diff(j)-c(j)diff(j-1))/dx)/2dx(x方向)+其他方向
diff_im(i,j) = diff_im(i,j)+...
delta_t*(...
(1/(2*dy^2))*(exp(-(((diff_im(i,j+1)-diff_im(i,j))/(kappa*dy)).^2))*(diff_im(i,j+1)-diff_im(i,j))-exp(-(((diff_im(i,j)-diff_im(i,j-1))/(kappa*dy)).^2))*(diff_im(i,j)-diff_im(i,j-1)))+...
(1/(2*dx^2))*(exp(-(((diff_im(i+1,j)-diff_im(i,j))/(kappa*dx)).^2))*(diff_im(i+1,j)-diff_im(i,j))-exp(-(((diff_im(i,j)-diff_im(i-1,j))/(kappa*dx)).^2))*(diff_im(i,j)-diff_im(i-1,j)))+...
(1/(2*dd^2))*(exp(-(((diff_im(i+1,j+1)-diff_im(i,j))/(kappa*dd)).^2))*(diff_im(i+1,j+1)-diff_im(i,j))-exp(-(((diff_im(i,j)-diff_im(i-1,j-1))/(kappa*dd)).^2))*(diff_im(i,j)-diff_im(i-1,j-1)))+...
(1/(2*dd^2))*(exp(-(((diff_im(i+1,j-1)-diff_im(i,j))/(kappa*dd)).^2))*(diff_im(i+1,j-1)-diff_im(i,j))-exp(-(((diff_im(i,j)-diff_im(i-1,j+1))/(kappa*dd)).^2))*(diff_im(i,j)-diff_im(i-1,j+1)))...
);
end
end
% 迭代的警告
fprintf('\rIteration %d\n',t);
end
LMFPM法
function diff_im = LMF_PM(im, num_iter, delta_t, kappa,mf_k)
%myec_ns 经典PM模型的4方向扩散
% DIFF_IM = LMF_PM(IM, NUM_ITER, DELTA_T, KAPPA, OPTION)
% 该函数执行基于中值滤波的灰度图像上的各向异性扩散(MF_PM模型),被认为是一个二维的网络结构的4个方向的扩散传导。
%
% 参数描述:
% IM - 灰度图 (MxN).
% NUM_ITER - 迭代次数
% DELTA_T - 迭代系数
% KAPPA - 控制传导的梯度模阈值。控制平滑。
% 扩散函数c(x,y,t) = exp(-(gards(mf_diff_im)/kappa).^2)
% 输出描述:
% DIFF_IM - 具有最大尺度空间参数的(扩散)图像。
% MF_K - 中值滤波所占线性影响比例,范围为[0,1]
%
% 使用例子:
% -------------
% s = phantom(512) + randn(512);
% num_iter = 15;
% delta_t = 1/7;%越大越平滑
% kappa = 20;%越大越平滑
% ad = LMF_PM(s,num_iter,delta_t,kappa);
% figure, subplot 121, imshow(s,[]), subplot 122, imshow(ad,[]);
% 转换输入图像类型为double.
im = double(im);
[M,N]=size(im);
% PDE(偏微分方程)的初始条件。
diff_im = im;
% 中心像素距离。
dx = 1;
dy = 1;
dd = sqrt(2);
% 各向异性扩散
for t = 1:num_iter %迭代次数
% 每次迭代都引入中值滤波
mf_diff_im = (1-mf_k).*diff_im + mf_k.*medfilt2(diff_im,[3,3]);
for i=2:M-1
for j=2:N-1 %迭代元素
% 在竖直,水平,左右斜方,这四个方向进行两次差分并在第一次差分时带入扩散函数,即
% (diff(t+1)-diff(t))/dt=
% ((c(j+1)diff(j+1)-c(j+1)diff(j))/dx - (c(j)diff(j)-c(j)diff(j-1))/dx)/2dx(x方向)+其他方向
diff_im(i,j) = diff_im(i,j)+...
delta_t*(...
(1/(2*dy^2))*(exp(-(((mf_diff_im(i,j+1)-mf_diff_im(i,j))/(kappa*dy)).^2))*(diff_im(i,j+1)-diff_im(i,j))-...
exp(-(((mf_diff_im(i,j)-mf_diff_im(i,j-1))/(kappa*dy)).^2))*(diff_im(i,j)-diff_im(i,j-1)))+...
(1/(2*dx^2))*(exp(-(((mf_diff_im(i+1,j)-mf_diff_im(i,j))/(kappa*dx)).^2))*(diff_im(i+1,j)-diff_im(i,j))-...
exp(-(((mf_diff_im(i,j)-mf_diff_im(i-1,j))/(kappa*dx)).^2))*(diff_im(i,j)-diff_im(i-1,j)))+...
(1/(2*dd^2))*(exp(-(((mf_diff_im(i+1,j+1)-mf_diff_im(i,j))/(kappa*dd)).^2))*(diff_im(i+1,j+1)-diff_im(i,j))-...
exp(-(((mf_diff_im(i,j)-mf_diff_im(i-1,j-1))/(kappa*dd)).^2))*(diff_im(i,j)-diff_im(i-1,j-1)))+...
(1/(2*dd^2))*(exp(-(((mf_diff_im(i+1,j-1)-mf_diff_im(i,j))/(kappa*dd)).^2))*(diff_im(i+1,j-1)-diff_im(i,j))-...
exp(-(((mf_diff_im(i,j)-mf_diff_im(i-1,j+1))/(kappa*dd)).^2))*(diff_im(i,j)-diff_im(i-1,j+1)))...
);
end
end
% 边界处理
diff_im(1,:)=mf_diff_im(1,:);
diff_im(M,:)=mf_diff_im(M,:);
diff_im(:,1)=mf_diff_im(:,1);
diff_im(:,N)=mf_diff_im(:,N);
% 迭代的警告
fprintf('\rIteration %d\n',t);
end
主程序
%% 基础处理
clc;clear;close;
i = imread('C:\Users\Administrator\Desktop\ec_noise\图片\lena.png');
% i = imread('C:\Users\Administrator\Desktop\ec_noise\图片\men.bmp');
if ndims(i)>2
i = i(:,:,2);
end
%% 加噪
% s=imnoise(i,'salt',0.01); %加噪(此处为椒盐噪声)
% s=imnoise(i,'gaussian',0.01); %加噪(此处为高斯噪声)
s=imnoise(i,'poisson'); %加噪(此处为泊松噪声)
s=imnoise(s,'gaussian',0.01); %加噪(此处为混合噪声)
%% 对比直接用中值和均值去噪
g3=imfilter(s,ones(3,3)/9);
g4=medfilt2(s,[3,3]);
%% 微分去噪
num_iter =10;%遍历次数
delta_t = 0.1;%越大越平滑,对应单次遍历时造成影响的系数
kappa = 15;%越大越平滑,保留边缘结构用小的
ad = myec_ns(s,num_iter,delta_t,kappa);
%% 在中值去噪的基础上再用微分方程去噪
mf_k=0.9;%中值滤波所占线性影响比例
m_ad = LMF_PM(s,num_iter,delta_t,kappa,mf_k);
%% 绘制
subplot 231, imshow(i,[]);
xlabel('原图');
subplot 234, imshow(s,[]);
xlabel('高斯+椒盐噪声图');
subplot 232,imshow(g3,[]);
xlabel('均值去噪');
subplot 235,imshow(g4,[]);
xlabel('中值去噪');
subplot 233, imshow(ad,[]);
xlabel('P-M去噪');
subplot 236, imshow(m_ad,[]);
xlabel('LMFPM去噪');
%% 图像去噪评价
%psnr评价
psnr_s = PSNR(s,i);
psnr_ave = PSNR(g3,i);
psnr_mid = PSNR(g4,i);
psnr_diff = PSNR(ad,i);
psnr_md = PSNR(m_ad,i);
% fprintf('\nPSNR:\ts:%f,\tave:%f,\tmid:%f,\tdiff:%f,\tmd:%f\n',psnr_s,psnr_ave,psnr_mid,psnr_diff,psnr_md)
fprintf('\nPSNR:\t%f\t%f\t%f\t%f\t%f\n',psnr_s,psnr_ave,psnr_mid,psnr_diff,psnr_md)
% mssim评价
K = [0.01,0.03];
L = 255;
window=[0.043542,0.0566406,0.043542;0.0566406,0.0707355,0.0566406;0.043542,0.0566406,0.043542];%对应高斯函数的sigma=1.5的3×3模板
[mssim_s, ssim_map_s] = MSSIM(s, i, K, window, L);
[mssim_ave, ssim_map_ave] = MSSIM(g3, i, K, window, L);
[mssim_mid, ssim_map_mid] = MSSIM(g4, i, K, window, L);
[mssim_diff, ssim_map_diff] = MSSIM(ad, i, K, window, L);
[mssim_md, ssim_map_md] = MSSIM(m_ad, i, K, window, L);
% fprintf('\nMSSIM:\ts:%f,\t\tave:%f,\tmid:%f,\tdiff:%f,\tmd:%f\n',mssim_s,mssim_ave,mssim_mid,mssim_diff,mssim_md)
fprintf('\nMSSIM:\t%f\t%f\t%f\t%f\t%f\n',mssim_s,mssim_ave,mssim_mid,mssim_diff,mssim_md)
% snr评价
snr_s = SNR(double(i),double(s));
snr_ave = SNR(double(i),double(g3));
snr_mid = SNR(double(i),double(g4));
snr_diff = SNR(double(i),double(ad));
snr_md = SNR(double(i),double(m_ad));
% fprintf('\nSNR:\ts:%f,\t\tave:%f,\tmid:%f,\tdiff:%f,\tmd:%f\n',snr_s,snr_ave,snr_mid,snr_diff,snr_md)
fprintf('\nSNR:\t%f\t%f\t%f\t%f\t%f\n',snr_s,snr_ave,snr_mid,snr_diff,snr_md)
参考文献
[1] PERONA P,MALIK J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639
[2] 杨春玲,陈冠豪,谢胜利. 基于梯度信息的图像质量评判方法的研究[J]. 电子学报,2007,35(7):1313-1317. DOI:10.3321/j.issn:0372-2112.2007.07.017.
[3] 佟雨兵,张其善,祁云平. 基于PSNR与SSIM联合的图像质量评价模型[J].中国图象图形学报, 2006,11(12):1758-1763. DOI:10.3969/j.issn.1006-8961.2006.12.003.
[4] 褚江,陈强,杨曦晨. 全参考图像质量评价综述[J]. 计算机应用研究,2014,31(1):13-22. DOI:10.3969/j.issn.1001-3695.2014.01.003.
[5] 李志伟,陈燕梅,张胜元. 基于SNR的数字图像置乱程度评价方法[J]. 厦门大学学报(自然科学版),2006,45(4):484-487. DOI:10.3321/j.issn:0438-0479.2006.04.010.
[6] 王超. 基于变分问题和偏微分方程的图像处理技术研究[D]. 安徽:中国科学技术大学,2007. DOI:10.7666/d.y1077961.
[7] 华珊,陈研,梁露焘,等. 利用基于偏微分方程的图像滤波技术研究土壤孔隙结构[J]. 农业工程学报,2014(3):78-85. DOI:10.3969/j.issn.1002-6819.2014.03.011.
[8] 崔丽娜,潘振宽,魏伟波,等. 基于PM模型的曲面去噪变分水平集方法[J]. 中国图象图形学报A,2010,15(3):361-366.
[9] 王毅,张良培,李平湘. 各向异性扩散平滑滤波的改进算法[J]. 中国图象图形学报,2006,11(2):210-216. DOI:10.3969/j.issn.1006-8961.2006.02.010.
[10] 付丽娟,姚宇,付忠良. 中值滤波与各向异性扩散相结合的医学图像滤波方法[J]. 计算机应用,2014,34(1):145-148. DOI:10.11772/j.issn.1001-9081.2014.01.0145.
[11] WANG Z,BOVIKAC,SHEIKH H R,et al.Image qualityassessment: from error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13( 4) : 600-612.
版权归原作者 Thorn玫瑰 所有, 如有侵权,请联系我们删除。