python数据分析与挖掘实战（财政收入影响因素分析及预测）

导言

   随着信息化的发展和科学技术的进步，数据分析与挖掘技术开始得到广泛应用。人们无时无刻不面对着海量的数据，这些海量数据中隐藏着人们所需要的具有决策意义的信息。数据分析与挖掘技术的产生和发展就是帮助人们利用这些数据，并从中发现隐藏的有用的信息。
    在此背景下，本文主要运用数据分析与挖掘技术对市财政收人进行分析，挖掘其中隐藏的运行模式，并对未来两年的财政收入进行预测，希望能够帮助政府合理地控制财政收支，优化财源建设，为制定相关决策提供依据。

这篇文章采用了ARIMA和灰色预测算法（GM11+SVR）两种算法进行财政收入模型的构建和预测。

一、ARIMA算法：

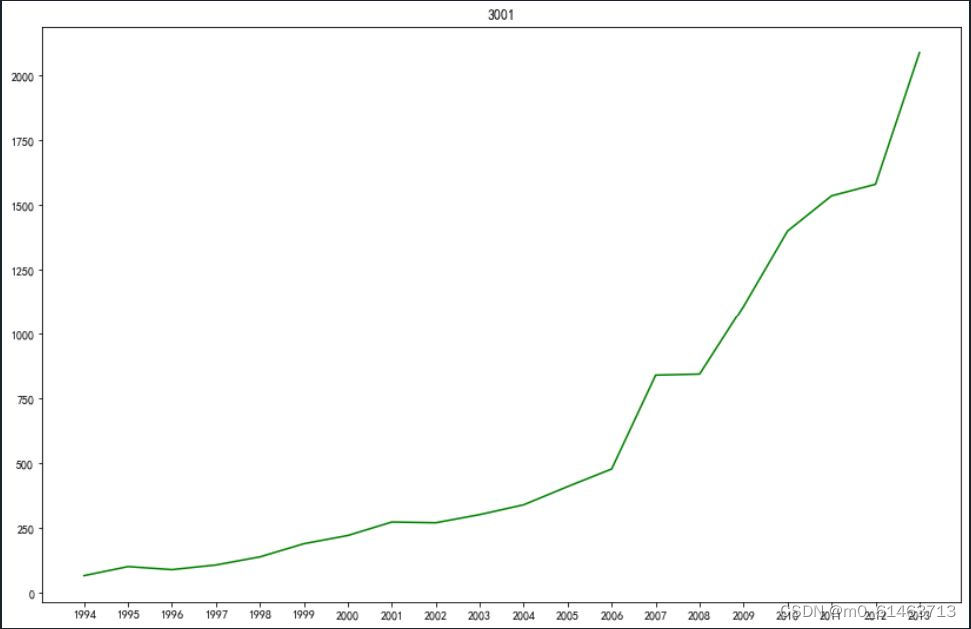
导包，读取数据集，将数据用图像表示出来

import pandas as pd
import numpy as np

data = pd.read_csv('D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\data.csv')

#原数据图像
import matplotlib.pyplot as plt 
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号

x = ['1994','1995','1996','1997','1998','1999','2000','2001','2002','2003','2004','2005','2006','2007','2008','2009','2010','2011','2012','2013']
y = data['y']
plt.figure(figsize=(14,9)) 
plt.plot(x,y,color='green')
plt.title('3001')
plt.show()

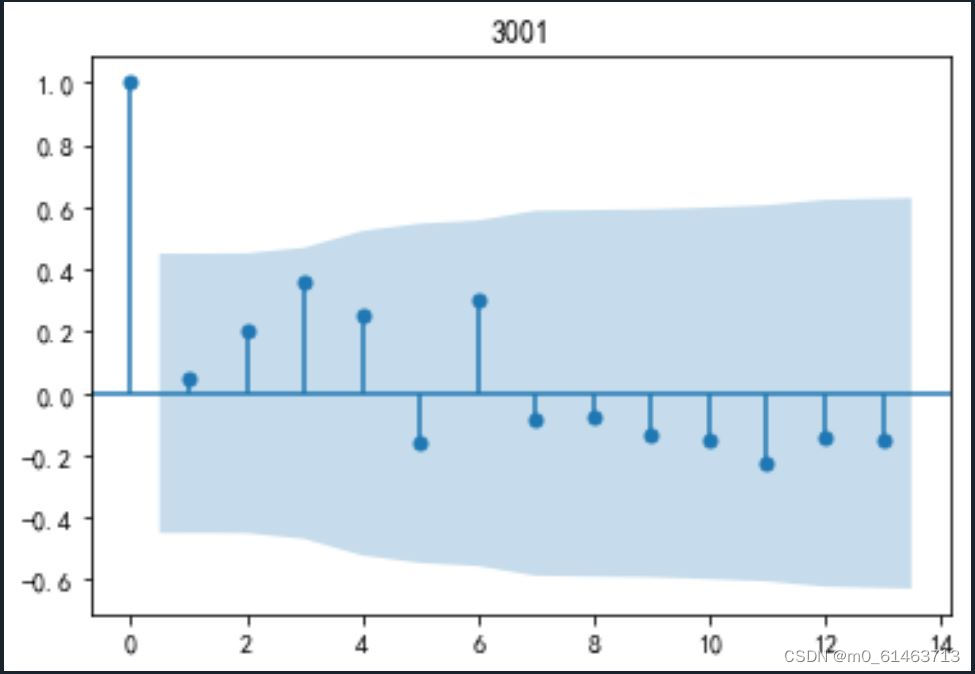
自相关、平稳性检测、差分的代码和图像：

#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(y.dropna()).show()
plt.title('3001')

# 平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print('ADF检验结果为：', ADF(y))

# 差分结果
df = y.diff()
plt.figure(figsize=(14,9)) 
plt.plot(x,df)
plt.title('3001')
plt.show()

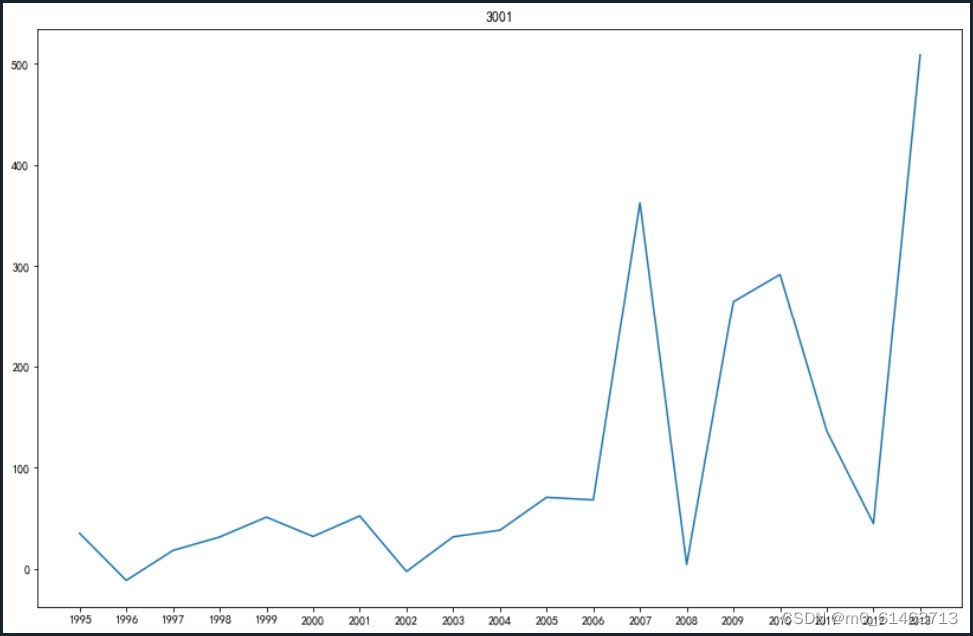
接下来对得到的财政收入差分结果进行自相关、平稳性、白噪声检测。

df=df.dropna() 

# 自相关图
plot_acf(df).show()
plt.title('3001')

# 平稳性检测
print('差分序列的ADF检验结果为：', ADF(df)) 

# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print('差分序列的白噪声检验结果为：', acorr_ljungbox(df, lags=1))

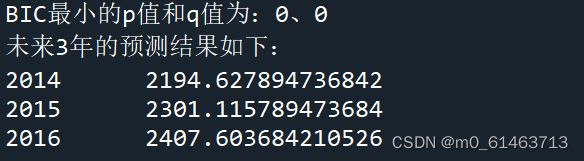
最后进行定阶、模型的构建、输出预测结果：

from statsmodels.tsa.arima_model import ARIMA
# 定阶
pmax = int(len(df)/10)  # 一般阶数不超过length/10
qmax = int(len(df)/10)  # 一般阶数不超过length/10
bic_matrix = []  # BIC矩阵
for p in range(pmax+1):
    temp = []
    for q in range(qmax+1):
        try:  
            temp.append(ARIMA(y, order=(p,1,q)).fit().bic)
        except:
            temp.append(None)
        bic_matrix.append(temp)
        
bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值
p,q = bic_matrix.stack().astype(float).idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。
print('BIC最小的p值和q值为：%s、%s' %(p,q)) 
model = ARIMA(y, order=(p,1,q)).fit()  # 建立ARIMA模型
key = model.forecast(3)[0]

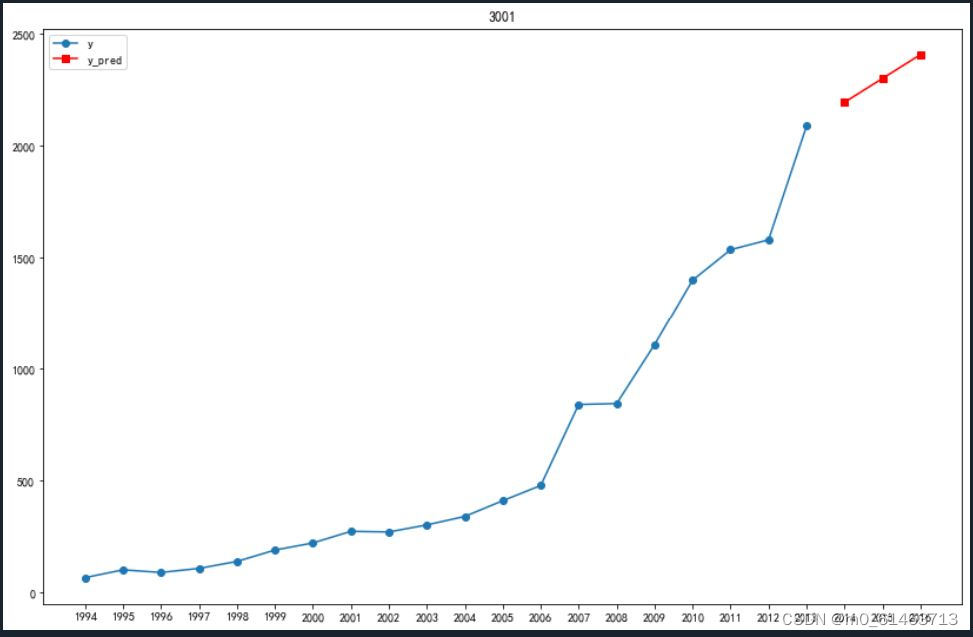
print('未来3年的预测结果如下：', 
      '\n2014     ',key[0],
      '\n2015     ',key[1],
      '\n2016     ',key[2])

我们可以将预测结果保存到文件中，并将其用图像表示出来：

#输出文件
data.index = range(1994,2014)
data.loc[2014,'y_pred'] = key[0]
data.loc[2015,'y_pred'] = key[1]
data.loc[2016,'y_pred'] = key[2]
data.to_csv('D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\new_data.csv')

#原图像与预测图象
plt.figure(figsize=(14,9)) 
x = ['1994','1995','1996','1997','1998','1999','2000','2001','2002','2003','2004','2005','2006','2007','2008','2009','2010','2011','2012','2013','2014','2015','2016']
plt.plot(x,data['y'],label='y',marker='o')
plt.plot(x,data['y_pred'],color='red',label='y_pred',marker='s')
plt.legend() #显示实例
plt.title('3001')
plt.show()

二、灰色预测算法:

描述性统计分析：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  #用来正常显示中文标签
#plt.rcParams['axes.unicode_minus'] = False  #用来正常显示负号
data = pd.read_csv("D:\\WeChat_Documents\\WeChat Files\\wxid_jv3alwxs4zwr22\\FileStorage\\File\\2023-03\\data.csv")

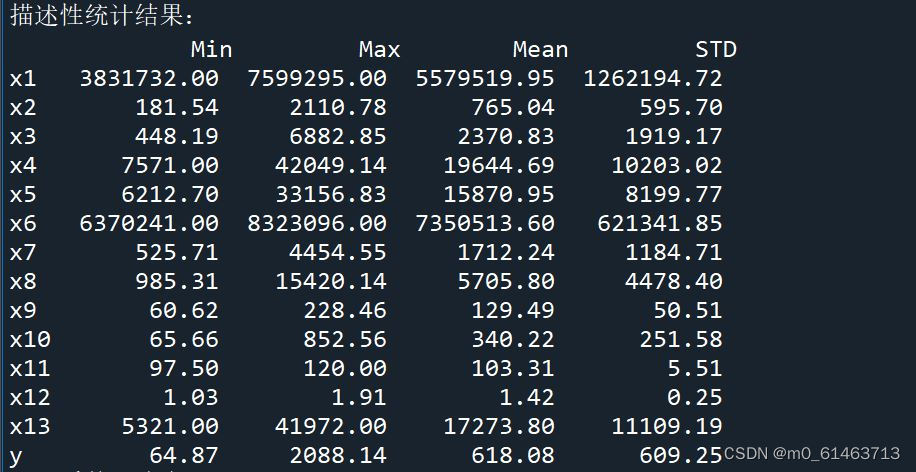
#描述性统计分析
#依次计算最小值、最大值、均值、标准差
describtion = [data.min(),data.max(),data.mean(),data.std()]
#将结果存入数据框
describtion = pd.DataFrame(describtion,index = ['Min','Max','Mean','STD']).T
print('描述性统计结果：\n',np.round(describtion,2))     #保留两位小数

求解原始数据的Pearson相关系数矩阵：

#代码清单6-2
corr = data.corr(method='pearson')  #计算相关系数矩阵
print('相关系数矩阵为: \n',np.round(corr,2))

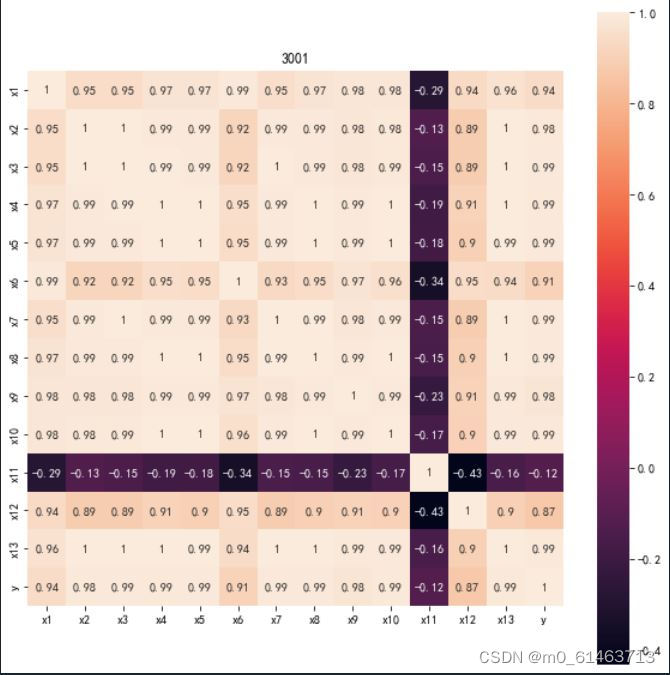
绘制相关热力图：

#代码清单6-3
import matplotlib.pyplot as plt
import seaborn as sns
plt.subplots(figsize=(10,10)) #设置画面大小
sns.heatmap(corr,annot=True,vmax=1,square=True)
plt.title('相关性热力图')
plt.title('3001')
plt.show()
plt.close

Lasso回归选取关键属性：

#代码清单6-4
import numpy as np
import pandas as pd
from sklearn.linear_model import Lasso

data = pd.read_csv('D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\data.csv')                    #读取数据
lasso = Lasso(1000)                     #调用函数
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为：',np.round(lasso.coef_,5)) #输出结果，保留5位小数

print('相关系数非零个数为：',np.sum(lasso.coef_ !=0)) #计算相关系数非零的个数            

mask = lasso.coef_ !=0                  #返回一个相关系数是非为零的布尔数组
print('相关系数是否为零: ',mask)          #
mask = np.append(mask,True)

new_reg_data = data.iloc[:,mask]
new_reg_data.to_csv('D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\new_reg_data.csv')
print('输出数据的维度为:',new_reg_data.shape) #查看输出数据的维度

构建灰色预测模型并预测（GM11）：

import sys
sys.path.append('D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03')    #设置路径
import numpy as np
import pandas as pd
from GM11 import GM11

inputfile1 = r'D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\new_reg_data.csv'  # 输入的数据文件
inputfile2 = r'D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\data.csv'  # 输入的数据文件
new_reg_data = pd.read_csv(inputfile1, index_col = 0,header =0)  # 读取经过特征选择后的数据
data = pd.read_csv(inputfile2, header=0)  # 读取总的数据
new_reg_data.index = range(1994, 2014)
new_reg_data.loc[2014] = None
new_reg_data.loc[2015] = None
new_reg_data.loc[2016] = None
l = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
for i in l:
  f = GM11(new_reg_data.loc[range(1994, 2014),i].values)[0]
  new_reg_data.loc[2014,i] = f(len(new_reg_data)-1)  # 2014年预测结果
  new_reg_data.loc[2015,i] = f(len(new_reg_data))  # 2015年预测结果
  new_reg_data.loc[2016, i] = f(len(new_reg_data)+1)  # 2016年预测结果
  new_reg_data[i] = new_reg_data[i].round(2)  # 保留两位小数

y = list(data['y'].values)  # 提取财政收入列，合并至新数据框中
y.extend([np.nan,np.nan,np.nan])
new_reg_data['y'] = y
outputfile = 'D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\new_reg_data_GM11.xls'  # 灰色预测后保存的路径
new_reg_data.to_excel(outputfile)  # 结果输出
print('预测结果为：\n',new_reg_data.loc[2014:2016,])  # 预测结果展示

构建支持向量回归预测模型（SVR）：

import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR

inputfile = 'D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\new_reg_data_GM11.xls'  # 灰色预测后保存的路径
data = pd.read_excel(inputfile, index_col=0, header=0)  # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']  # 属性所在列
#data.index = range(1994, 2014)
data_train = data.loc[range(1994,2014)].copy()  # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std  # 数据标准化
x_train = data_train[feature].values  # 属性数据
y_train = data_train['y'].values  # 标签数据
linearsvr = LinearSVR()  # 调用LinearSVR()函数
linearsvr.fit(x_train,y_train)
x = ((data[feature] - data_mean[feature])/data_std[feature]).values  # 预测，并还原结果。
data['y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
data.to_excel('D:\\WeChat_Documents\\WeChat Files\\FileStorage\\File\\2023-03\\new_reg_data_GM11_revenue.xls')

print('真实值与预测值分别为：\n',data[['y','y_pred']])

fig = data[['y','y_pred']].plot(subplots = False, style=['b-o','r-*'])  # 画出预测结果图
plt.title('3001')
plt.show()