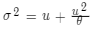Seurat-SCTransform用于单细胞表达矩阵的标准化,但并不能用于去除样本间的批次效应。
教程:Using sctransform in Seurat (satijalab.org)
Introduction to SCTransform, v2 regularization • Seurat (satijalab.org)
kim解释:Kimi.ai - 帮你看更大的世界 (moonshot.cn)
不能去批次
Apply sctransform normalization
- Note that this single command replaces , , and .
NormalizeData``````ScaleData``````FindVariableFeatures - Transformed data will be available in the SCT assay, which is set as the default after running sctransform
- During normalization, we can also remove confounding sources of variation, for example, mitochondrial mapping percentage
1️⃣ 一个SCTransform函数即可替代NormalizeData, ScaleData, FindVariableFeatures三个函数;
2️⃣ 对测序深度的校正效果要好于log标准化(10万以内的细胞都建议使用SCT);
3️⃣ SCTransform,可用于矫正线粒体、细胞周期等因素的影响,但不能用于批次矫正;
4️⃣ 改善信/噪比;
5️⃣ 发现稀有细胞。
Seurat | 强烈建议收藏的单细胞分析标准流程(SCTransform normalization)(四)-CSDN博客
教程
1)数据详见
③单细胞学习-pbmc的Seurat 流程_seurat 删除离散细胞-CSDN博客
library(Seurat)
library(ggplot2)
library(sctransform)
#Load data and create Seurat object
pbmc_data <- Read10X(data.dir = "../data/pbmc3k/filtered_gene_bc_matrices/hg19/")
pbmc <- CreateSeuratObject(counts = pbmc_data)
2)Apply sctransform normalization
# store mitochondrial percentage in object meta data
pbmc <- PercentageFeatureSet(pbmc, pattern = "^MT-", col.name = "percent.mt")
# run sctransform
pbmc <- SCTransform(pbmc, vars.to.regress = "percent.mt", verbose = FALSE)
3)降维

4)优势
用户可以根据规范标记单独注释集群。但是,与标准 Seurat 工作流程相比,sctransform 归一化在以下几个方面揭示了更明显的生物学差异:
- 根据 CD8A、GZMK、CCL5、GZMK 表达,可清晰分离至少 3 个 CD8 T 细胞群(幼稚细胞、记忆细胞、效应细胞)
- 基于 S100A4、CCR7、IL32 和 ISG15 的三种 CD4 T 细胞群(幼稚、记忆、IFN 激活)的清晰分离
- 基于 TCL1A、FCER2 的 B 细胞簇中的其他发育子结构
- 基于 XCL1 和 FCGR3A 将 NK 细胞额外分离成 CD56dim 与明亮的簇。
# These are now standard steps in the Seurat workflow for visualization and clustering Visualize
# canonical marker genes as violin plots.
VlnPlot(pbmc, features = c("CD8A", "GZMK", "CCL5", "S100A4", "ANXA1", "CCR7", "ISG15", "CD3D"),
pt.size = 0.2, ncol = 4)

# Visualize canonical marker genes on the sctransform embedding.
FeaturePlot(pbmc, features = c("CD8A", "GZMK", "CCL5", "S100A4", "ANXA1", "CCR7"), pt.size = 0.2,
ncol = 3)
SCTransform方法原理
R tips:Seurat之SCTransform方法原理 (qq.com)
sctransform是指的一个Normalize方法,这个方法可以使用sctransform包中vst函数实现,这个函数接受的对象是一个matrix或者dgcMatrix等counts对象;
SCTransform是Seurat包中的一个函数,它可以直接对Serutat对象进行sctransform处理,本质上这个函数就是调用的sctransform包中vst函数进行的Normalize。
LogNormalize是什么?
LogNormalize:
Feature counts for each cell are divided by the total counts for that cell and multiplied by the scale.factor.
This is then natural-log transformed using log1p.
scale.factor: 10000
所以LogNormalize就做了两个处理:每个细胞除以各自的Counts总数再乘以一个scale.factor值10000,然后使用自然对数进行取对数处理。
本质上这个LogNormalize就是一个最简单的测序深度的Normalize,那就是假定所有细胞的测序深度都是相同的(每个细胞除以自己的Counts总数就会将Counts总数变为1),然后再乘以10000,则从数据上将每个细胞的Counts总数调整为10000。然后再按照Counts的传统,对它进行log处理即可(变为常规的线性可加的数据)。
为什么sctransform优于LogNormalize
LogNormalize的测序深度相等的假设就是一个硬伤,细胞类型、细胞周期等因素的不同,那么细胞表达的基因数量就可能不同。相比较直接规定一个均一的Counts总值(LogNormalize方法就是相当于规定每个细胞都表达了10000个feature counts),更好的策略是使用一个模型建模每个基因在每个细胞中表达的实际Counts值和一个细胞总Counts值的关系。
Seurat中使用的模型如下:
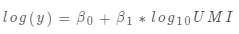
,这里的UMI代表一个细胞的所有Counts的加和,这个UMI在Seurat中叫做潜变量(latent variable)。
如果你去看的sctransform的vst函数的说明文档,可以发现默认的潜变量latent_vat就是log_umi。
当拟合出来这个模型后,==就可以从真是Counts值中减去拟合值,得到的残差就是校正过测序深度的值了==,每个基因的Counts再除以它的标准差就是一个方差稳定Normalize Counts数据了。
一般情况下,Counts数据都是建模的负二项分布。
对于离散数据的发生次数的模型最常见和很容易想到的是泊松分布,这个模型确实在早期的RNA-seq数据中有被使用过,但是很明显泊松分布并不合适,原因就在于泊松分布的均值和方差相等,但是如果实际看RNA-seq数据的话,会发现随着均值的增加,每个基因的方差越来越大超过了均值。单细胞RNA-seq趋势和RNA-seq数据类似,也是同样的情况。
为了正确拟合这种情况,就需要使用一个overdispersion的分布,比如负二项分布。负二项分布有一个超参数theta值,用于控制方差(sigma^2)超出均值(mu)的程度:
。
如果你去看sctransform::vst的帮助文档会发现一个参数叫做exclude_poisson,也就是说建模或处理模型过程中会去除poisson分布的基因,这些基因的特征就是mu < 0.001或者mu > variance,之所以mu > variance就代表它不是负二项分布基因是因为负二项分布是overdispersion分布,它的方差是大于均值的。
在Seurat中,它是通过三步法来完成这个Normalize过程的:
(1)使用一个GLM拟合出每个gene的Counts值和log_umi的关系,这个过程会获得上面说的公式的β0和β1,并获得拟合值fitted;默认情况下,这里是拟合的一个泊松模型,因为第二步会做一个正则化处理,第一步获得的参数是一个预参数,实际结果差异不大;根据原始值y和fitted值,可以使用MASS::theta.ml函数获得负二项分布theta的估计;
(2)使用一个高斯核回归拟合基因的几何平均值和获得的theta值、模型系数beta的关系;
(3)使用负二项分布回归重新拟合数据,确切的说这一步不是拟合,而是根据获得的系数beta,带入方程求得拟合的fitted值(这个fitted值就是负二项分布的均值mu),然后y减去fitted获得残差值,根据刚才的公式获得方差值,相除得到Pearson residuals值,也就是Normalize的值。
第一步详解:我们已经知道SCTranform的实际Normalize过程是调用的sctransform::vst函数,第一步拟合的代码在下面,可以发现实际代码是get_model_pars函数,get_model_pars中可以看到这里有多种拟合method可以选择,默认是possion,原因也是上述所说的,一个是运行速度的考虑,另外是由于第二步还要进行正则化,possion和负二项的拟合结果的最终差异不太大。sctransform文献中(10.1186/s13059-019-1874-1)也有这方面的描述,虽然第一步拟合的模型差别是有的,但是最终第三步获得的Pearson residuals的差异微乎其微。
While the estimated model parameters can vary slightly between these methods, the resulting Pearson residuals are extremely similar.
#1. sctransform::vst,关键代码是调用了get_model_pars获得拟合的参数
# ...省略...
model_pars <- get_model_pars(genes_step1, bin_size, umi,
model_str, cells_step1, method, data_step1, theta_given,
theta_estimation_fun, exclude_poisson, fix_intercept,
fix_slope, use_geometric_mean, use_geometric_mean_offset,
verbosity)
# ...省略...
#2. sctransform:::get_model_pars
# ...省略...
par_lst <- future_lapply(X = index_lst, FUN = function(indices) {
umi_bin_worker <- umi_bin[indices, , drop = FALSE]
if (fix_intercept | fix_slope) {
mu_bin_worker <- mu_bin[indices, , drop = FALSE]
model_pars_bin_worker <- model_pars_bin[indices,
, drop = FALSE]
intercept_bin_worker <- model_pars_bin_worker[,
"(Intercept)"]
slope_bin_worker <- model_pars_bin_worker[, "log_umi"]
}
if (method == "poisson") { # <==== 默认poisson方法 ==== #
return(fit_poisson(umi = umi_bin_worker, model_str = model_str,
data = data_step1, theta_estimation_fun = theta_estimation_fun))
}
if (method == "qpoisson") {
# ...省略...
}
if (method == "nb_theta_given") {
# ...省略...
}
if (method == "nb_fast") {
# ...省略...
}
if (method == "nb") {
# ...省略...
}
if (method == "glmGamPoi") {
# ...省略...
}
if (method == "glmGamPoi_offset") {
# ...省略...
}
}, future.seed = TRUE)
# ...省略...
//3. fit_poisson方法最终调用的函数是使用C++写的
List qpois_reg(NumericMatrix X, NumericVector Y, const double tol, const int maxiters,
const double minphi, const bool returnfit){
const unsigned int n=X.nrow(), pcols=X.ncol(), d=pcols;
arma::colvec b_old(d, arma::fill::zeros), b_new(d), L1(d), yhat(n), y(Y.begin(), n, false), m(n), phi(n);
arma::vec unique_vals;
arma::mat L2, x(X.begin(), n, pcols, false), x_tr(n, pcols);
double dif;
// ...省略...
x_tr=x.t();
int ij=2;
for(dif=1.0;dif>tol;){ /* 关键求解过程,迭代数值求解*/
yhat=x*b_old;
m=(exp(yhat));
phi=y-m;
L1=x_tr*phi;
L2=x.each_col()%m;
L2=x_tr*L2;
b_new=b_old+solve(L2,L1,arma::solve_opts::fast);
dif=sum(abs(b_new-b_old));
b_old=b_new;
if(++ij==maxiters)
break;
}
double p=sum(arma::square(phi)/m)/(n-pcols);
NumericVector coefs = NumericVector(b_new.begin(), b_new.end());
coefs.names() = colnames(X);
List l;
l["coefficients"]=coefs;
l["phi"]=p;
l["theta.guesstimate"]=mean(m)/(std::max(p, minphi)-1);
if(returnfit){
l["fitted"]=NumericVector(m.begin(), m.end());
}
return l;
}
第二步详解:调用reg_model_pars函数进行正则化,使用的方法是建模theta、beta值与基因均值之间的关系,然后使用这里建模回归的拟合值作为真正的theta、beta值。拟合方法使用的是高斯核回归(R中的ksmooth函数来完成的)。高斯核回归可以理解为就是一个对数据做平滑处理。
R中的ksmooth函数有一个示例,直接在R中复制既可运行,可以看到两条平滑曲线对数据点的拟合:
with(cars, {
plot(speed, dist)
lines(ksmooth(speed, dist, "normal", bandwidth = 2), col = 2)
lines(ksmooth(speed, dist, "normal", bandwidth = 5), col = 3)
})将此图对应到本例中,可以认为第一步获得的值就是此图的散点值,正则化后的值就是此图中高斯核回归线上的点。
这也是为什么第一步的建模方法是possion还是nbinomial分布不是太重要的原因。
另外高斯核回归的参数中,banwidth也很重要(参看ksmooth示例图的两条平滑曲线的不同),所以vst函数使用了bw.SJ函数用于预测这个值。
#1. sctransform::vst,关键代码是调用了reg_model_pars对第一步获得的拟合参数进行正则化
# ...省略...
if (do_regularize) {
model_pars_fit <- reg_model_pars(model_pars, genes_log_gmean_step1,
genes_log_gmean, cell_attr, batch_var, cells_step1,
genes_step1, umi, bw_adjust, gmean_eps, theta_regularization,
genes_amean, genes_var, exclude_poisson, fix_intercept,
fix_slope, use_geometric_mean, use_geometric_mean_offset,
verbosity)
model_pars_outliers <- attr(model_pars_fit, "outliers")
}
else {
model_pars_fit <- model_pars
model_pars_outliers <- rep(FALSE, nrow(model_pars))
}
# ...省略...
#2. sctransform:::reg_model_pars
# ...省略...
bw <- bw.SJ(genes_log_gmean_step1) * bw_adjust
x_points <- pmax(genes_log_gmean, min(genes_log_gmean_step1))
x_points <- pmin(x_points, max(genes_log_gmean_step1))
o <- order(x_points)
model_pars_fit <- matrix(NA_real_, length(genes), ncol(model_pars),
dimnames = list(genes, colnames(model_pars)))
model_pars_fit[o, "dispersion_par"] <- ksmooth(x = genes_log_gmean_step1,
y = model_pars[, "dispersion_par"],
x.points = x_points,
bandwidth = bw,
kernel = "normal")$y
# ...省略...
第三步详解:虽然说第三步是一个负二项分布的拟合,其实就是带入拟合好的theta、beta值,求得pearson residual值。
#1. sctransform::vst,默认是获得pearson_residual残差
# ...省略...
for (i in 1:max_bin) {# max_bin,就是默认以500个基因为一组进行计算,一组叫做一个bin
genes_bin <- genes[bin_ind == i]
# mu就是fitted值
mu <- exp(tcrossprod(model_pars_final[genes_bin, -1, drop = FALSE], regressor_data_final))
# y就是原始counts值
y <- as.matrix(umi[genes_bin, , drop = FALSE])
if (min_variance == "model_mean") {
# ...省略...
}
else if (min_variance == "model_median") {
# ...省略...
}
else { # <==== 默认情况 ==== #
res[genes_bin, ] <- switch(residual_type,
pearson = pearson_residual(y, mu, model_pars_final[genes_bin, "theta"], min_var = min_var),
deviance = deviance_residual(y, mu, model_pars_final[genes_bin, "theta"]),
stop("residual_type ", residual_type, " unknown - only pearson and deviance supported at the moment"))
}
if (verbosity > 1) {
setTxtProgressBar(pb, i)
}
}
# ...省略...
#2. sctransform:::pearson_residual
function (y, mu, theta, min_var = -Inf)
{
model_var <- mu + mu^2/theta # 负二项分布的方差的公式
model_var[model_var < min_var] <- min_var
return((y - mu)/sqrt(model_var)) # 残差除以标准差即是pearson residual值
}
如何直观理解sctransform方法?
回忆一下刚才的拟合模型
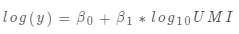
,第一步和第二步就是获得了这个模型中的beta值(也就是β0和β1)以及模型的overdispersion估计theta值,那么将beta和实际的log_umi值带入模型就可以得到拟合的值fitted,其实这个拟合的值就是对负二项分布的均值的衡量,也就是mu。
那么第三步就是方才说的将这些参数带入模型求得pearson residual值。为何pearson residual值是对生物学效应的正确估计?首先Counts的值会受到细胞测序深度的影响,这个影响的表现就是log_umi,那么根据拟合的模型得到log_umi的fitted值,这个fitted就代表了log_umi的影响,那么从原始Counts减去这个影响所得到的残差值就代表了真实的生物学效应。为了获得一个方差稳定变换结果,这个残差值还除以了标准差做了标准化处理。
简而言之:Counts ~ log_umi + biology_infomation,那么Counts减去log_umi的影响就是真正的生物学效应信息了。
SCTransform的下游使用场景的细节
Seurat对象在经过SCTransform处理后会增加一个SCT的Assay,里面的scaled.data就是经过scale之后的pearson residual值,这个值是用于后续降维聚类分析使用的。另外默认情况下,SCTransform还会对UMI进行correct并放置到SCT的counts中,这个correct值的log之后就是SCT assay中的data值,这个data值是用于差异表达及可视化使用的,这里的可视化主要是指的表达量可视化如vlnplot、featureplot等。
UMI进行correct的原理也很简单,和sctransform的第三步类似,它会将log_umi的值指定为所有细胞的中位数,也就是说固定了log_umi的值。然后将pearson residual乘以标准差之后再加上这个值即可。
未尽信息:
(1)多个SCTransform后的Seurat对象merge之后的结果,只是简单的合并表达数据的行与列,无法直接用于差异表达和可视化;
(2)基于SCTransform合并数据集的integrated结果,它的integrated assay可以用于降维聚类,但是无法用于差异表达,它的SCT assay其实只是简单的进行了Seurat对象的merge,也无法直接用于差异表达和可视化。
版权归原作者 hx2024 所有, 如有侵权,请联系我们删除。