关于通过matlab实现Canny边缘处理的一些笔记

最近看了一些神经网络处理图像的视频，受到卷积核的启发，突然对图像处理感兴趣，于是就单从边缘检测算法入手，学习了比较高级的Canny边缘处理，也通过matlab实现了Canny边缘处理。

相比较于通过soble算子sx和sy处理，提取水平和竖直边缘信息，平方和相加开根号得到的边缘提取图像，canny边缘算法具有一下优势：

1.解决了边缘过宽问题

左图为普通边缘处理，右图为Canny算法处理

可以看到明显的单层边界线

2.去除了部分噪点

下面记录一下主要流程和相关函数

1.导入并处理rgb图片

如A = imread('Figure.jpg') ， 从目录下的文件中找到图片，导入。

此时A为三维rgb数据，判断维度函数为 **ndims(A)**，返回值为维度。

导入图片矩阵格式一般为int8，需要再转化为double形式，否则矩阵计算中会出现问题，比如sqrt(imgx.^2+imgy.^2)计算中报错，显示输入数据格式不对。

使用**im2double(A)**函数转化为double形式。

随后将rgb图片转化为灰度值图片：

使用 B = rgb2gray(A);

部分代码如下

    %判断是否为rgb图片，是则转化为灰度图
    if ndims(preimg)==3
        preimg=im2double(preimg);
        grayimg=rgb2gray(preimg); %转化为灰度图
    else
        grayimg=preimg;
    end

2.高斯滤波

对图像进行平滑模糊处理，更容易检测出边缘

利用高斯分布的矩阵，卷积原图

fspecial函数生成高斯分布矩阵H

%高斯滤波
H=fspecial('gaussian',[2*k+1,2*k+1],c); 
imgG=imfilter(grayimg, H, 'replicate');

k为高斯矩阵外围层数，c为方差

k根据图像实际情况调整，实际上k越大代表一个像素与周围像素关联性越大，所以边缘较清晰的k值小。

c越大，图像越模糊

k值均为7，上图方差为1，下图为5

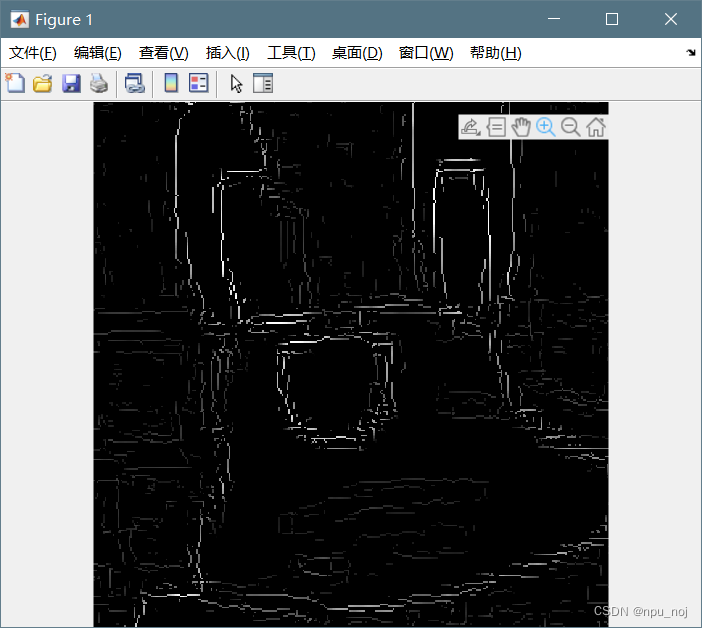
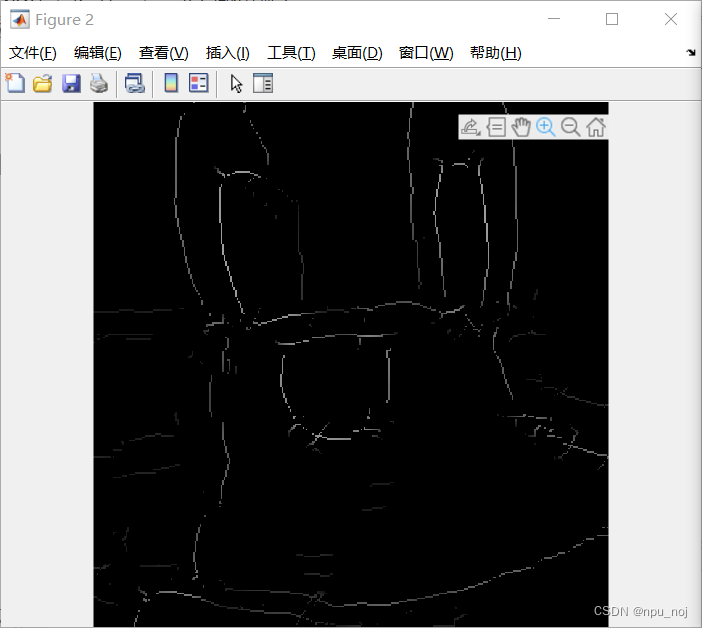
可以看出，高斯处理不足导致边界检测模糊，很难形成一条线

3.计算梯度和梯度方向

使用soble算子sx,sy计算在x方向和y方向梯度（imgx，imgy）以及梯度方向G_d

梯度方向通过atan函数求得

    %梯度计算
    sx=[1 0 -1;2 0 -2;1 0 -1];
    imgx=imfilter(imgG,sx,'replicate');
    sy=[1 2 1; 0 0 0;-1 -2 -1];
    imgy=imfilter(imgG,sy,'replicate');
    %梯度值
    G=sqrt(imgx.^2+imgy.^2);
    %梯度方向
    G_d=atand(imgy./imgx);
    %给空值赋0
    for y=1:size(G,1)
        for x=1:size(G,2)
            if ismissing(G_d(y,x))
                G_d(y,x)=90;
            end
        end
    end

这里会有个小问题，就是imgx值为0时，得到梯度方向为NaN，此时通过ismissing函数判断数据是否为NaN，手动设置为90度。

之后判断梯度方向，从上下，到/，到左右，到\依次定义为1，2，3，4

注意：这里的梯度角度和开始设置的x，y方向有关

%判断梯度方向
%梯度方向分别为上下,左右,/，\,
    G_s=zeros(size(grayimg,1),size(grayimg,2));
    for y=1:size(G_d,1)
        for x=1:size(G_d,2)
            if (G_d(y,x)> 67.5 & G_d(y,x)<= 90 )| (G_d(y,x)< -67.5 & G_d(y,x)>= -90)
                G_s(y,x)=1;
            end
            if (G_d(y,x)> 22.5 & G_d(y,x)<= 67.5 )
                G_s(y,x)=2;
            end
            if (G_d(y,x)>= -22.5 & G_d(y,x)<= 22.5 )
                G_s(y,x)=3;
            end
            if (G_d(y,x)>= -66.5 & G_d(y,x)< -22.5 )
                G_s(y,x)=4;
            end
        end
    end

从而得到方向矩阵G_s

4.非极大值抑制NMS

这一步操作是为了减小边缘粗细

判断梯度方向上的值的大小，如果比梯度方向值小，则令其值为0

也就是挑选出边缘上梯度最大的一条线，从而减小边缘粗细

    %非极大值抑制
    %添加0边
    G0=zeros(size(G,1)+2,size(G,2)+2);
    G0(2:(size(G,1)+1),2:(size(G,2)+1))=G;
    G_d=G;
    for y=1:size(G,1)
        for x=1:size(G,2)
            if G_s(y,x)==1
                if G0(y+1,x+1) < max(G0(y+1+1,x+1),G0(y+1-1,x+1))
                    G_d(y,x)=0;
                end
            end
            if G_s(y,x)==2
                if G0(y+1,x+1) < max(G0(y+1-1,x+1+1),G0(y+1+1,x+1-1))
                    G_d(y,x)=0;
                end
            end
            if G_s(y,x)==3
                if G0(y+1,x+1) < max(G0(y+1,x+1-1),G0(y+1,x+1+1))
                    G_d(y,x)=0;
                end
            end
            if G_s(y,x)==4
                if G0(y+1,x+1) < max(G0(y+1+1,x+1+1),G0(y+1-1,x+1-1))
                    G_d(y,x)=0;
                end
            end
        end
    end

这里添加0边是为了在之后比较时数组不超界

5.双阈值处理

为了减小噪声，过滤部分无关信息，采用双阈值处理，大于阈值时保持不变，小于阈值时置0，在阈值中间时，判断周围8格内是否有大于阈值的像素，如果有则不变，否则置0

这里高阈值一般在0.3到0.5，较暗图像取0.1

低阈值一般小于0.1，这个随具体情况而定

    %双阈值处理

    G_t=G_d;
    %加个边
    G0=zeros(size(G,1)+2,size(G,2)+2);
    G0(2:(size(G,1)+1),2:(size(G,2)+1))=G_d;
    for y=1:size(G_d,1)
        for x=1:size(G_d,2)
            if G_d(y,x)>=TH
            elseif G0(y,x)<= TL
                G_t(y,x)=0;
            elseif G0(y,x)> TL & G0(y,x)< TH
                if (G0(y+1,x+1)>=TH | G0(y+1,x)>=TH | G0(y+1,x-1)>=TH | G0(y,x+1)>=TH ...
                        | G0(y,x-1)>=TH | G0(y-1,x+1)>=TH | G0(y-1,x)>=TH | G0(y-1,x-1)>=TH)
                    else
                        G_t(y,x)=0;
                end
            end
        end
    end

这里同样加了0边，防止超界

最后封装函数，变量设为preimg（图片矩阵），TH、TL为阈值，k，c为高斯处理时矩阵层数和方差。

函数默认TH、TL、k、c分别为0.5、0.1、1、1， 一般较大的图片k值设置为4-15，c值1-10

可以通过结果修改参数，以达到最好的效果！