K-means与DBSCAN聚类算法
前言:目前数据聚类方法大体上可以分为划分式聚类方法(Partition-based Methods)、基于密度的聚类方法(Density-based methods)、层次化聚类方法(Hierarchical Methods)及一些聚类的新方法等四类,而在本模块中我们学习的K-means聚类算法属于划分式聚类方法、DBSCAN聚类算法属于基于密度的聚类方法,另一系统聚类法,也称层次聚类法,属于层次化聚类方法。随着算法领域的不断发展,也产生了量子聚类、核聚类等新聚类方法。
一、K-means聚类算法
1.优缺点
在讲K-means聚类算法之前,我想先交代一下它的缺点。
优点:(1)相对来说较为简单,易实现
(2)对处理大数据集,该算法是相对高效率的(当然这里的“大”也是有 限度的,如果数据集过大,就要使用Mini Batch K-Means算法了)
(3)可解释度较强(为什么这么说呢,其实主要还是从数学角度来讲的,它的步骤可以说是有较强的数学支撑的)
缺点:(1)这个算法的k值是要求提前给定的(那么我们就想了,都没聚类去哪找k值呢?答案是经验与个人感觉,我一般的做法是猜测+Spss跑一下测试看看哪个k值较优)
(2)对异常点较为敏感(因为要计算距离所以不难想到)
(3)较易受初始聚类中心的影响
(4)……
当然缺点不止这些,仅列出影响较大的缺点。
2.步骤
老规矩,我们用流程图表示K-means的步骤。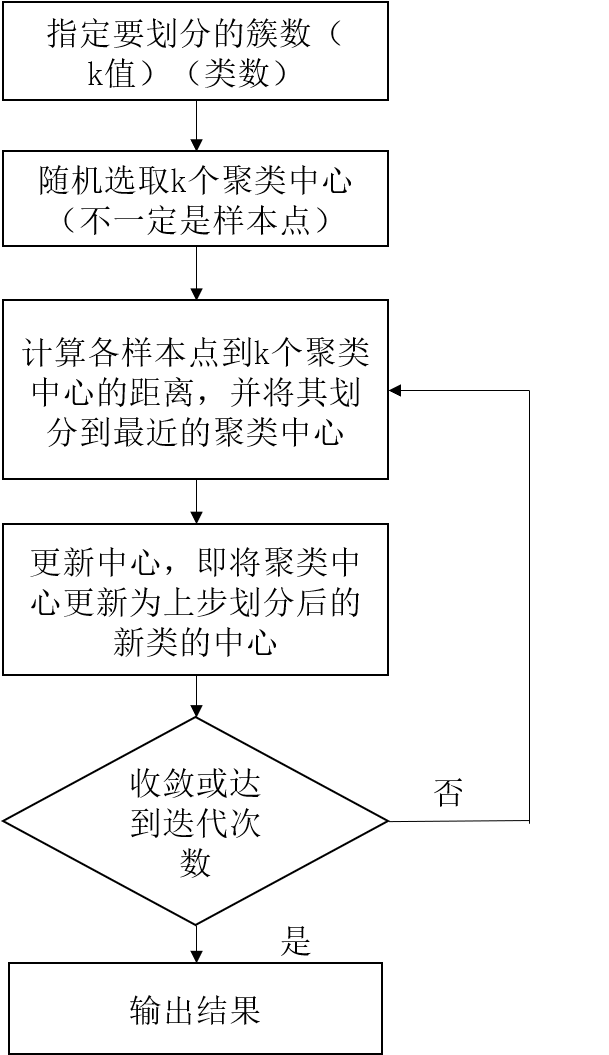
3.Spss实现
聚类的这一部分我们统一用Spss软件来实现,原因是内置了集成化的各种统计功能较为方便。
(1)实现步骤
数据集:【金山文档】 测试数据 https://kdocs.cn/l/cbfmkbJGAyYm
数据集的导入,可查阅系统聚类法一节。
*[数据取自嵩天Python机器学习算法]
选择k-均值聚类
选择“聚类成员”与“与聚类中心的距离”
选择“每个个案的聚类信息”
(2)结果分析
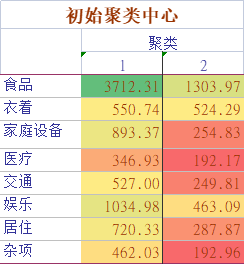

对于这次聚类,可见聚类结果为两类,我们可解释为:高消费省份与低消费省份。而对于聚类,难的就在于如何去解释聚类结果,这是极为重要的,否则聚类将没有意义。
值得注意的是,从第一个表格中可以看出,初始聚类中心选择为上海和内蒙古,这是否真的是随机选择呢?可以说不是,Spss默认使用了K-means++算法。
这里还是来介绍一下:
K-means++算法与K-means算法的区别在于初始k个聚类中心的选取原则不同,K-means++算法选择初始聚类中心的原则是:初始的聚类中心之间的相互距离要尽可能远。
步骤:
在数据集中随机选取一个样本点作为第一个聚类中心
计算出样本点与已有聚类中心的距离,距离越大,被选中作为聚类中心的概率也越大
依照概率来抽选下一个聚类中心
重复步骤二和三直至选出k个聚类中心
这个算法也改善了K-means算法的一些缺点,如对初值和孤立点数据值敏感。
二、DBSCAN聚类算法
1.定义
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在噪声的空间数据库中发现任意形状的聚类。
2.步骤
考虑到本算法的流程较难理解,本处我用通俗的语言来叙述一下并推荐一个国外的可视化网站。
我先对这个算法做一些简单的解释:
输入:样本集D,邻域参数(epsilon,minPoints)
输 出 :簇的划分C
E邻域:以样本点为中心,epsilon为半径的领域
minPoints:可以理解为点的一个阈值
核心点:E领域内点的个数(包括自身)大于等于minPoints的的点
边界点:E领域内点的个数(包括自身)小于minPoints且属于其他核心点领域内的点
噪音点:既不是核心点也不是噪音点的点
它的大概步骤是这样的:首先我们选择两个参数:epsilon(通俗地理解为半径)与minPoints;然后,我们从数据集中随机选择一个点,如果 E邻域内样本点数(包括原始点本身)大于等于minPoints ,就可以开始了;接着,我们检查邻域内的所有点并查看它们的类型,如果不是噪音点那么可以逐步扩展类,之后的点也是按照这个步骤进行的,读者可以类推一下。
可视化网站:
[https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/]
3.伪代码
DBSCAN(D, Eps, MinPts)
Begin
init C=0; //初始化簇的个数为0
for each unvisited point p in D
mark p as visited; //将p标记为已访问
N = getNeighbours (p, Eps);
if sizeOf(N) < MinPts then
mark p as Noise; //如果满足sizeOf(N) < MinPts,则将p标记为噪声
else
C= next cluster; //建立新簇C
ExpandCluster (p, N, C, Eps, MinPts);
end if
end for
End
其中ExpandCluster算法伪码如下:
ExpandCluster(p, N, C, Eps, MinPts)
add p to cluster C; //首先将核心点加入C
for each unvisited point p’ in N
mark p' as visited;
N’ = getNeighbours (p’, Eps); //对N邻域内的所有点在进行半径检查
if sizeOf(N’) >= MinPts then
N = N+N’; //如果大于MinPts,就扩展N的数目
end if
if p’ is not member of any cluster
add p’ to cluster C; //将p' 加入簇C
end if
end for
End ExpandCluster
*[源自Baidu百科 ]
通俗的讲,使用伪代码的目的就是使代码可以用任意一种编程语言轻松的实现,因为伪代码的可读性要求很高。
4.Matlab推荐的代码
[https://ww2.mathworks.cn/matlabcentral/fileexchange/52905‐dbscan‐clustering‐algorithm]
注:另外需指出的是,DBSCAN算法对于epsilon和minPoints敏感,这两个参数也较难确定。
在进行聚类之前,还是希望有一个宏观的把控,因此数据的预处理表现得更加重要了,可以先对数据做一个散点图,观察一下表现形式。
当然少不了的是新春祝福!!!
愿 律回春晖渐 万象始更新
版权归原作者 caiggle 所有, 如有侵权,请联系我们删除。