线性代数 linear algebra

2.3 实现属于我们自己的向量

Vector.py

class Vector:
def init(self, lst):
```
 self._values = lst    
```
#return len
def len(self):
return len(self._values)
#return index th item
def getitem(self, index):
return self._values[index]
#direct use call this method
def repr(self):
return "Vector({})".format(self._values)
#print call this method
def str(self):
return "({})".format(", ".join(str(e) for e in self._values))

main_vector.py

import sys
import numpy
import scipy
from playLA.Vector import Vector
if name == "main":
```
 vec = Vector([     5, 2])
```
```
 print(vec)    
```
```
 print(len(vec))    
```

 print(     "vec[0] = {}, vec[1] = {}".format(vec[0], vec[1]))

2.5 实现向量的基本运算

Vector.py

class Vector:
def init(self, lst):
```
 self._values = lst    
```
#return len
def len(self):
return len(self._values)
#return index th item
def getitem(self, index):
return self._values[index]
#direct use call this method
def repr(self):
return "Vector({})".format(self._values)
#print call this method
def str(self):
return "({})".format(", ".join(str(e) for e in self._values))
#vector add method
def add(self, another):
assert len(self) == len(another),"lenth not same"
return Vector([a + b for a, b in zip(self._values, another._values)])
return Vector([a + b for a, b in zip(self, another)])
#迭代器设计_values其实是私有成员变量，不想别人访问，所以使用迭代器
#单双下划线开头体现在继承上，如果类内内部使用的变量使用单下划线
def iter(self):
return self._values.iter()
#sub
def sub(self, another):
return Vector([a + b for a, b in zip(self._values, another._values)])
return Vector([a - b for a, b in zip(self, another)])
#self * k
def mul(self, k):
return Vector([k * e for e in self])
k * self
def rmul(self, k):
return Vector([k * e for e in self])
#取正
def pos(self):
return 1 * self
#取反
def neg(self):
return -1 * self

main_vector.py

import sys
import numpy
import scipy
from playLA.Vector import Vector
if name == "main":
```
 vec = Vector([     5, 2])
```
```
 print(vec)    
```
```
 print(len(vec))    
```

 print(     "vec[0] = {}, vec[1] = {}".format(vec[0], vec[1]))

```
 vec2 = Vector([     3, 1])
```

 print(     "{} + {} = {}".format(vec, vec2, vec + vec2))

 print(     "{} - {} = {}".format(vec, vec2, vec - vec2))

 print(     "{} * {} = {}".format(vec, 3, vec * 3))

 print(     "{} * {} = {}".format(3, vec, vec * 3))

 print(     "-{} = {}".format(vec, -vec))

 print(     "+{} = {}".format(vec, +vec))

2.8 实现0向量

Vector.py

@classmethod
def zero(cls, dim):
return cls([0] * dim)

main_vector.py

```
 zero2 = Vector.zero(     2)
```
```
 print(zero2)    
```

 print(     "{} + {} = {}".format(vec, zero2, vec + zero2))

3.2实现向量规范

Vector.py

self / k
def truediv(self, k):
return Vector((1 / k) * self)
#模
def norm(self):
return math.sqrt(sum(e**2 for e in self))
#归一化
def normalize(self):
if self.norm() < EPSILON:
raise ZeroDivisionError("Normalize error! norm is zero.")
return Vector(self._values)/self.norm()

main_vector.py

 print(     "normalize vec is ({})".format(vec.normalize()))

```
 print(vec.normalize().norm())    
```
try :
```
 zero2.normalize()    
```
except ZeroDivisionError:

 print(     "cant normalize zero vector {}".format(zero2))

3.3 向量的点乘

3.5实现向量的点乘操作

Vector.py

def dot(self, another):
assert len(self) == len(another), "Error in dot product. Length of vectors must be same."
return sum(a * b for a, b in zip(self, another))

main_vector.py

print(vec.dot(vec2))

3.6向量点乘的应用

3.7numpy中向量的基本使用

main_numpy_vector.py

import numpy as np
if name == "main":
```
 print(np.__version__)    
```
```
 lst = [     1, 2, 3]
```
```
 lst[     0] = "LA"
```
```
 print(lst)    
```
#numpy中只能存储一种数据
```
 vec = np.array([     1, 2, 3])
```
```
 print(vec)    
```
vec[0] = "LA"
vec[0] = 666
```
 print(vec)    
```
```
 print(np.zeros(     5))
```
```
 print(np.ones(     5))
```
```
 print(np.full(     5, 666))
```
```
 print(vec)    
```
```
 print(     "size = ", vec.size)
```
```
 print(     "size = ", len(vec))
```
```
 print(vec[     0])
```
```
 print(vec[     -1])
```
```
 print(vec[     0:2])
```
```
 print(type(vec[     0:2]))
```
#点乘
```
 vec2 = np.array([     4, 5, 6])
```

 print(     "{} + {} = {}".format(vec, vec2, vec + vec2))

 print(     "{} - {} = {}".format(vec, vec2, vec - vec2))

 print(     "{} * {} = {}".format(2, vec, 2 * vec))

 print(     "{} * {} = {}".format(vec, 2, vec * 2))

 print(     "{} * {} = {}".format(vec, vec2, vec * vec2))

 print(     "{}.dot({})= {}".format(vec, vec2, vec.dot(vec2)))

#求模
```
 print(np.linalg.norm(vec))    
```
```
 print(vec/ np.linalg.norm(vec))    
```

 print(np.linalg.norm(vec/ np.linalg.norm(vec)))

#为什么输出nan
```
 zero3 = np.zeros(     3)
```
```
 print(zero3 /np.linalg.norm(zero3))
```

4矩阵

4.2实现矩阵

Matrix.py

from .Vector import Vector
class Matrix:
#list2d二维数组
def init(self, list2d):

 self._values = [row[:]      for row in list2d]

def repr(self):
return "Matrix({})".format(self._values)
```
 __str__ = __repr__    
```
def shape(self):
return len(self._values),len(self._values[0])
def row_num(self):
return self.shape()[0]
def col_num(self):
return self.shape()[1]
def size(self):
```
 r, c = self.shape()    
```
return r * c
```
 __len__ = row_num    
```
def getitem(self, pos):
```
 r, c =pos    
```
return self._values[r][c]
#第index个行向量
def row_vector(self, index):
return Vector(self._values[index])
def col_vector(self, index):
return Vector([row[index] for row in self._values])

main_matrix.py

from playLA.Matrix import Matrix
if name == "main":
```
 matrix = Matrix([[     1, 2],[3, 4]])
```
```
 print(matrix)    
```

 print(     "matrix.shape = {}".format(matrix.shape()))

 print(     "matrix.size = {}".format(matrix.size()))

 print(     "matrix.len = {}".format(len(matrix)))

 print(     "matrix[0][0]= {}".format(matrix[0, 0]))

 print(     "{}".format(matrix.row_vector(0)))

 print(     "{}".format(matrix.col_vector(0)))

4.4 实现矩阵的基本计算

Matrix.py

def add(self, another):
assert self.shape() == another.shape(),"ERROR in shape"
return Matrix([[a + b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])
def sub(self, another):
assert self.shape() == another.shape(),"ERROR in shape"
return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])
def mul(self, k):
return Matrix([[e*k for e in self.row_vector(i)] for i in range(self.row_num())])
def rmul(self, k):
return self * k
#数量除法
def truediv(self, k):
return (1/k) * self
def pos(self):
return 1 * self
def neg(self):
return -1 * self
@classmethod
def zero(cls, r, c):
return cls([[0]*c for _ in range(r)])

main_matrix.py

 matrix2 = Matrix([[     5, 6], [7, 8]])

 print(     "add: {}".format(matrix + matrix2))

 print(     "sub: {}".format(matrix - matrix2))

 print(     "mul: {}".format(matrix * 2))

 print(     "rmul: {}".format(2 * matrix))

 print(     "zero_2_3:{}".format(Matrix.zero(2, 3)))

4.8实现矩阵乘法

Matrix.py

main_matrix.py

Matrix.py

def dot(self, another):
if isinstance(another, Vector):
assert self.col_num() == len(another), "error in shape"
return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])
if isinstance(another, Matrix):
assert self.col_num() == another.row_num(),"error in shape"
return Matrix([self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())] for i in range(self.row_num()))

main_matrix.py

```
 T = Matrix([[     1.5, 0], [0, 2]])
```
```
 p = Vector([     5, 3])
```

 print(     "T.dot(p)= {}".format(T.dot(p)))

 P = Matrix([[     0, 4, 5], [0, 0, 3]])

 print(     "T.dot(P)={}".format(T.dot(P)))

4.11 实现矩阵转置和Numpy中的矩阵

main_numpy_matrix.py

import numpy as np
if name == "main":
#创建矩阵
```
 A = np.array([[     1, 2], [3, 4]])
```
```
 print(A)    
```
#矩阵属性
```
 print(A.shape)    
```
```
 print(A.T)    
```
#获取矩阵元素
```
 print(A[     1, 1])
```
```
 print(A[     0])
```
```
 print(A[:,      0])
```
```
 print(A[     1, :])
```
#矩阵的基本运算
```
 B = np.array([[     5, 6], [7, 8]])
```
```
 print(A + B)    
```
```
 print(A - B)    
```
```
 print(     10 * A)
```
```
 print(A *      10)
```
```
 print(A * B)    
```
```
 print(A.dot(B))
```

5 矩阵进阶

5.3 矩阵变换

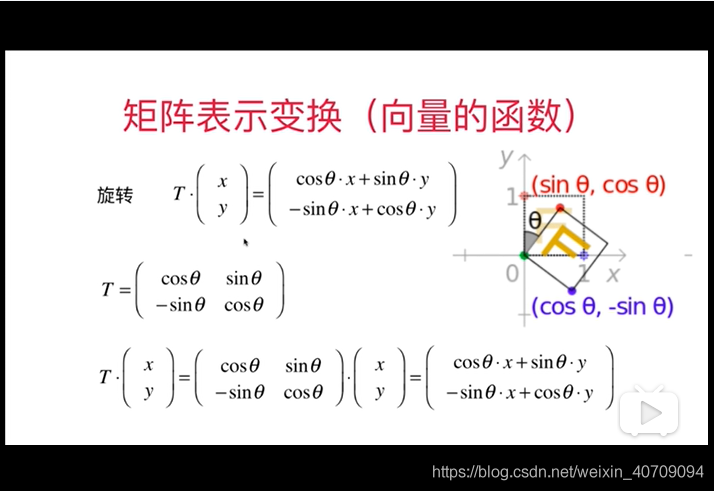
main_matrix_transformation.py

import math
import matplotlib.pyplot as plt
from playLA.Matrix import Matrix
from playLA.Vector import Vector
if name == "main":

  points = [[     0, 0], [0, 5], [3, 5], [3, 4], [1, 4],

  [     1, 3], [2, 3], [2, 2], [1, 2], [1, 0]]

  x = [point[     0] for point in points]

  y = [point[     1] for point in points]

```
  plt.figure(figsize=(     5, 5))
```
```
  plt.xlim(     -10, 10)
```
```
  plt.ylim(     -10, 10)
```
```
  plt.plot(x, y)    
```
plt.show()
```
  P = Matrix(points)    
```
T = Matrix([[2, 0], [0, 1.5]])#x扩大2倍，y扩大1.5倍
T = Matrix([[1, 0], [0, -1]])#关于X轴对称
T = Matrix([[-1, 0], [0, 1]])#关于X轴对称
T = Matrix([[-1, 0], [0, -1]])#关于原点对称
T = Matrix([[1, 0.5], [0, 1]])
T = Matrix([[1, 0], [0.5, 1]])
```
  theta = math.pi /      3
```
#旋转theta角度

  T = Matrix([[math.cos(theta), math.sin(theta)], [-math.sin(theta), math.cos(theta)]])

```
  P2 = T.dot(P.T())    
```

  plt.plot([P2.col_vector(i)[     0] for i in range(P2.col_num())],[P2.col_vector(i)[1] for i in range(P2.col_num())])

```
  plt.show()
```

5.6实现单位矩阵和numpy中的逆矩阵

Matrix.py

#单位矩阵
@classmethod
def identity(cls, n):
```
  m = [[     0]*n for _ in range(n)]
```
for i in range(n):
```
  m[i][i] =      1
```
return cls(m)

main_matrix.py

```
  I = Matrix.identity(     2)
```
```
  print(I)    
```

  print(     "A.dot(I) = {}".format(matrix.dot(I)))

  print(     "I.dot(A) = {}".format(I.dot(matrix)))

main_numpy_matrix.py

#numpy中的逆矩阵
```
  invA = np.linalg.inv(A)    
```
```
  print(invA)    
```
```
  print(A.dot(invA))    
```
```
  print(invA.dot(A))    
```
```
  C = np.array([[     1,2]])
```
```
  print(np.linalg.inv(C))
```

5.8用矩阵表示空间

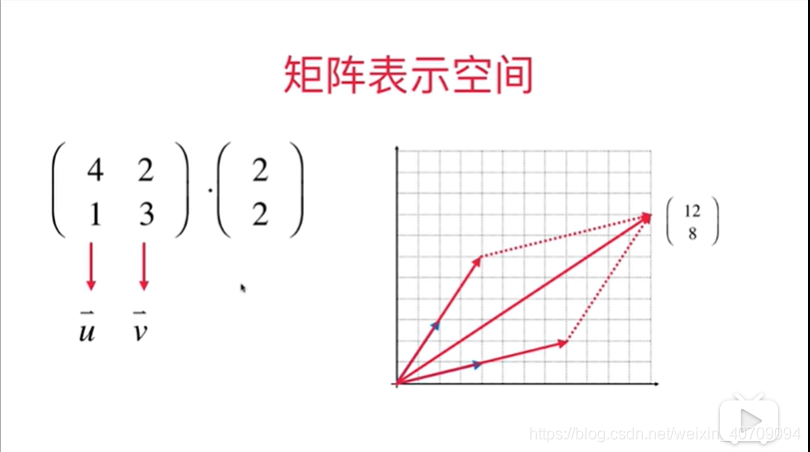
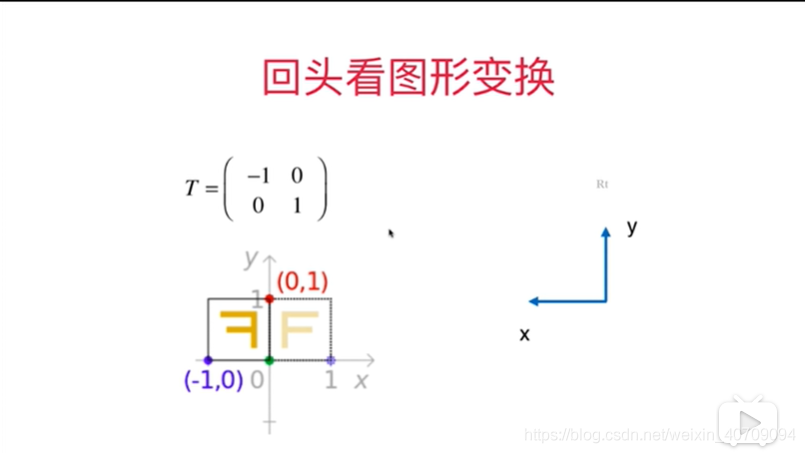
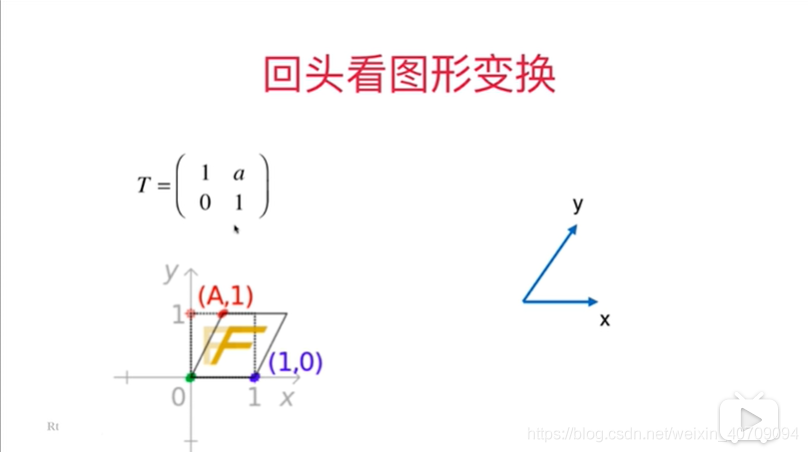
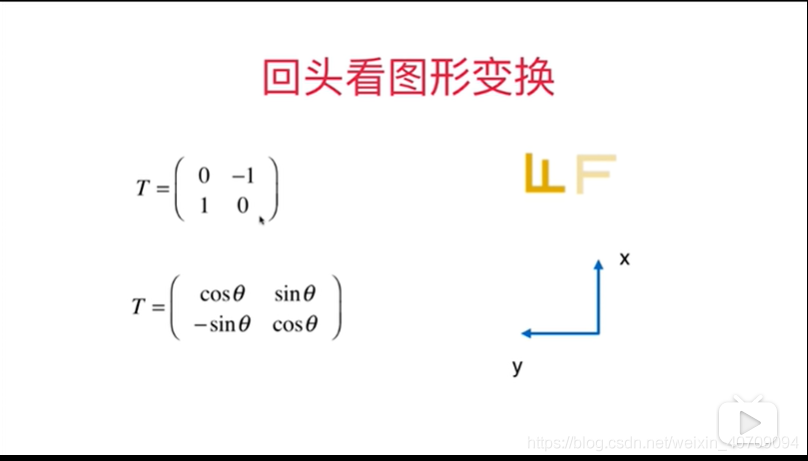
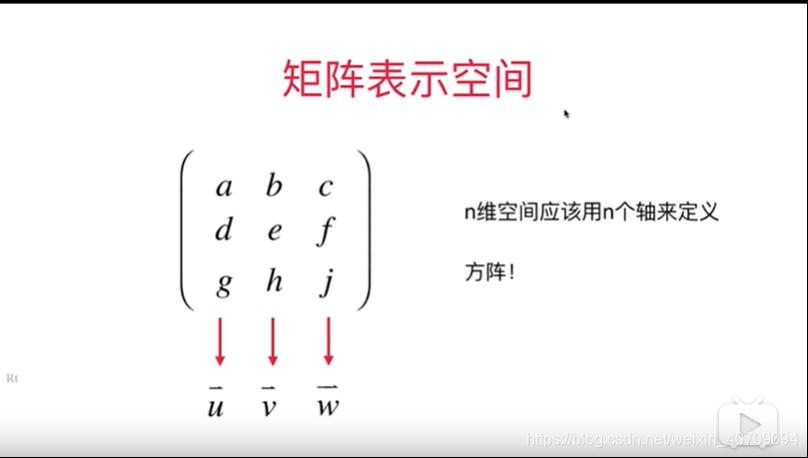
x轴就是(0，1)y轴就是(-1，0)

6 线性系统

6.4实现高斯-约旦消元法

https://blog.csdn.net/weixin_40709094/article/details/105602775

标签： python 机器学习 numpy

本文转载自: https://blog.csdn.net/weixin_45944896/article/details/118925705
版权归原作者 小石小石摩西摩西 所有，如有侵权，请联系我们删除。

线性代数 linear algebra

return Vector([a + b for a, b in zip(self._values, another._values)])

return Vector([a + b for a, b in zip(self._values, another._values)])

k * self

self / k

vec[0] = "LA"

vec[0] = 666

plt.show()

T = Matrix([[2, 0], [0, 1.5]])#x扩大2倍，y扩大1.5倍

T = Matrix([[1, 0], [0, -1]])#关于X轴对称

T = Matrix([[-1, 0], [0, 1]])#关于X轴对称

T = Matrix([[-1, 0], [0, -1]])#关于原点对称

T = Matrix([[1, 0.5], [0, 1]])

T = Matrix([[1, 0], [0.5, 1]])

发表评论

“线性代数 linear algebra”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航